Audiofanzine a 25 ans !
Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
FR
EN
Notifications
  • Refonte graphique octobre 2025
    Refonte graphique octobre 2025
    Une refonte graphique vient d'être mise en ligne. Nous espérons qu'elle vous plaira. Merci de nous signaler tout bug ou perte de fonctionnalité ici →
  • Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Pour célébrer notre quart de siècle, UVI se joint à nous et vous offre le Digital Synsations Vol.1. Pour en profiter c'est par ici 👉
  • Nouveauté : Bookmark article, news ou tuto
    Nouveauté : Bookmark article, news ou tuto
    Bookmarkez un article, une news ou un tuto et retrouvez-le dans votre section "Mes signets" du menu membre.
  • 6 nouveaux annuaires
    6 nouveaux annuaires
    Luthiers, Réparateurs, Cours de musique, Studios d’enregistrement, de mastering et de répétition... Suggérez l’ajout d’une entreprise, inscrivez la vôtre ou déposez un avis.
  • Alertes disponibilité et baisse de prix
    Alertes disponibilité et baisse de prix
    Ces nouvelles fonctionnalités vous permettent d'être informé·e dès qu'un produit est disponible ou que son prix a baissé.
  • Tentatives d'arnaque dans les petites annonces
    Nous faisons face depuis quelques mois à une recrudescence de tentatives d'arnaques dans les petites annonces. Suivez nos recommandations >
Techniques du Son
News
Articles
Médias
Forums
Tutoriels Tutos

Limiteur True Peak Numerique (Oversampling)

  • 19 réponses
  • 6 participants
  • 2 267 vues
  • 6 followers
Sujet de la discussion Limiteur True Peak Numerique (Oversampling)
Bonjour a tous,
Je bloque depuis un certain temps sur une notion...
Quand on parle d'oversampling/suréchantillonnage X4/X8/etc... pour un limiteur True Peak,
que ce passe il réellement ? on suréchantillonne quoi ?? on a deja des échantillons comment peut on les suréchantilloner.
J'ai vue que cette technique avait pour but de simuler les Peak possible lors de la CNA.
Parler de suréchantillonage serait il un abus de langage pour définir un algorithme imitant le lissage lors de la CNA ?

Bisous
2

Citation de Louenn

 Parler de suréchantillonage serait il un abus de langage pour définir un algorithme imitant le lissage lors de la CNA ?

 Absolument pas. Le suréchantillonnage n'est surtout pas une arnaque, ou un délire audiophile, ni un abus de langage ou quoi que ce soit de pas sérieux. C'est un moyen, en ajoutant des échantillons intermédiaires sur la base du calcul d'ajouter des infos sur ce qu'il se passe entre les échantillons. Cela permet plusieurs choses.

Tout d'abord, cela permet de quantifier dans le domaine numérique des valeurs intermédiaires très proches du signal reconstruit par un CNA, et d'indiquer les "true peak" sur un analyseur, ou pour un limiteur TP.

Et ça permet de diminuer le bruit audible de quantification lors de la reconstruction (en le déplaçant hors de la bande audible, et au delà de la limite definie par la loi de Shannon/Nyquist).

 

[ Dernière édition du message le 21/10/2017 à 14:06:54 ]

3
On créé des échantillon supplémentaire sur quelles bases, quel algorithme?
Comment peut on passer outre un pas de quantification défini par le convertisseur en amont ?

Merci de ta réponse !
4
Citation de Louenn :
On créé des échantillon supplémentaire sur quelles bases, quel algorithme?
Comment peut on passer outre un pas de quantification défini par le convertisseur en amont ?

On interpole.
Imagine que tu veux suréchantillonner avec un facteur 2.
Il te faut donc calculer, pour chaque paire d'échantillons une valeur intermédiaire.
Il suffit de dire que ces deux points sont reliés par une droite, une sinusoide, ou autre fonction continue (interpolation linéaire, cosinusoidale, bicubique, spline, etc...).
Tu sais que, sur l'axe du temps, la coordonnée de ton nouveau point est exactement à mi-chemin entre la coordonnée de tes deux points de référence et que ce point intermédiaire appartient à la fonction que tu utilises pour interpoler.
Connaissant cette valeur ainsi que les coordonnées de tes deux points de référence et l'équation de la fonction passant par ces deux points, tu peux calculer la coordonnée de ton point intermédiaire.

Resistance is not futile... it's voltage divided by current

5
d'accord !
il y a tout de même une marge d'erreur ? la fonction n'est pas normée ou définie pour le calcul ? si la fonction est définie, elle diverge en fonction du convertisseur ? (arbitré par l'utilisateur ou random ?)

merci encore !
6
Cet article expliquera les tenants et aboutissants bien mieux que je ne saurais le faire: https://ccrma.stanford.edu/~jos/resample/

Pour ma part, je n'ai jamais eu besoin d'autre chose que l'interpolation linéaire ou cosinusoidale qui sont simples à calculer (en nombre de cycles pour un processeur).

Resistance is not futile... it's voltage divided by current

[ Dernière édition du message le 21/10/2017 à 15:52:35 ]

7
Merci de ta réponse.
Je crois bien que je m'aventure un peu trop loin pour mes connaissances actuel, je vais quand même creuser la question.
En laissant de coté les techniques d'interpolations (si j'utilise correctement le terme), j'en revient au limiteur True Peak.
La fonction de suréchantillonage (interpolation des échantillon de base, du coup) tente au mieux de reproduire l'allure du signal analogique post CNA.
Imaginons que j'utilise un limiteur TP qui suréchantillonne avec un facteur 2 ( Fréquence échantillonnage de travail a 48 kHz ----> Freq du limiteur TP a 96 Khz)
Quelle action va avoir le limiteur sur un signal qu'il ne connait que par le biais d'un suréchantillonnage, il ne peut travailler que sur les échantillons de base soit ce défini par la fréquence d'échantillonage de la session.

Le Limiteur TP va donc atténuer les échantillons réel en fonction des échantillons trouvé par interpolation ?

j’espère être clair...


8
Je cherche une information sur le limiter V3 de la gamme Oxford de Sonnox.
Après avoir consulté la fiche technique du plug, je ne trouve pas d'information concernant le nombre "d'inter-échantillon" créé par le limiter pour ces mesures TP (freq de sur-échantillonnage), si quelqu'un pourrais éclairer ma lanterne cela serait top !
9
Attention, pour reconstituer les signaux audio échantillonnée on n'utilise pas d'interpolation linéaire, polynomiale ou sinusoïdale.
On utilise l'interpolation via sinus cardinale qui consiste à "remplacer" chaque échantillon par un sinus cardinal
(voir l'image) d'amplitude correspondante à la valeur de l'échantillon. Ceci peut aussi être vu comme l'application d'un filtre passe bas dans le domaine fréquentiel.

Une des chose importante à observer c'est que l'interpolation entre deux échantillons dépend de tous les échantillons et pas seulement des quelques-uns qui l'entourent.

Pour sur-échantillonner d'un facteur k on ajoute d'abord k-1 échantillons de valeur 0 entre chaque échantillon. On a bien multiplié par k le nombre d'échantillons. Manque plus qu'a leur donner "la bonne" valeur.
Pour ce faire on applique un filtre passe bas (tu peux lire ça, partie 3.7, pour voir le rapport). C'est l'étape d'interpolation.

Dans le document que aaB cite, il est discuter d'interpolation linéaire, mais il ne parle pas de l'interpolation du signal mais de l'interpolation du filtre passe bas.
C'est a dire que ce fameux filtre passe bas qui donne "les bonnes" valeurs au échantillons qu'on ajoute, comporte certaines difficultés d’implémentation qui sont résolus par l'interpolation linéaire des coefficients du filtre.
J'ai l'impression qu'il y a eu une confusion ?

Enfin j'attire votre attention sur la notation "sinc" utilisé dans le document précédant, qui veux dire sinus cardinal et pas sinus. Si on lis trop rapidement on peut zapper ;).

Figure-11-Fonction-sinus-cardinal.ppm

Citation :
Quelle action va avoir le limiteur sur un signal qu'il ne connait que par le biais d'un suréchantillonnage, il ne peut travailler que sur les échantillons de base soit ce défini par la fréquence d'échantillonage de la session.

Il va bien travailler sur le signal sur-échantillonné. A la fin du traitement le signal va être sous-échantillonné pour revenir à la fréquence du projet. Mais le traitement aura bien été fait en fonction sur signal sur-échantillonné.

[ Dernière édition du message le 21/10/2017 à 17:30:38 ]

10
Merci pour la réponse ! je vais lire attentivement la doc que tu viens d'envoyer en espérant comprendre !
Certaines notions pour moi sont extrêmement flou comme le sinus cardinal, interpolation linéaire, etc...

Au final, on revient sur la fréquence de la session, donc sur les "même" échantillons (atténué pour certains) que ce avant le traitement ?


11
L'interpolation linéaire des échantillons n'est absolument pas la méthode correcte pour trouver les "true peaks" ; elle n'apporte même rien

Une autre façon de dire ce qu'a expliqué Danbei est que l'on connait une information capitale sur le signal échantillonné : le signal numérisé à une fréquence de Fe a une largeur spectrale qui ne dépasse pas Fe/2.
Si ce n'est pas le cas, le signal continu ne pourrait pas être reconstruit à partir du signal échantillonné.

Cette borne nous permet de savoir exactement ce qu'il peut se passer entre deux échantillons. Je t'épargne les étapes mathématiques mais c'est ici qu'apparaît le sinus cardinal.
Il s'agit de l'autre versant du théorème de Nyquist-Shannon.
12
:?!: houlà c'est chaud là !!
Mais Danbei qu'est ce que ce filtre passe bas dont tu parles ? ?? :noidea: c'est celui qui se trouve à Fe/2??
13
On peut décrire un signal et les opérations faites dessus de deux manières équivalentes : dans le domaine temporel et dans le domaine fréquentiel.
Échantillonner dans le domaine temporel <=> Périodiser dans le domaine fréquentiel,
Interpoler par sinus cardinal dans le domaine temporel <=> Appliquer un filtre passe bas dans le domaine fréquentiel.

Il y a un autre filtre passe bas dans l'histoire, le filtre anti-repliement (c'est celui dont tu parle je pense).
Comme la dit Eratom, le processus d’échantillonnage/interpolation ou (périodisation/filtre passe bas, dans le domaine fréquentiel) ne fonctionne que si le spectre du signal est borné.
Ainsi, avant de faire tout ça il faut appliquer un filtre passe bas (le filtre anti-repliement) pour s'assurer d'avoir un spectre borné.

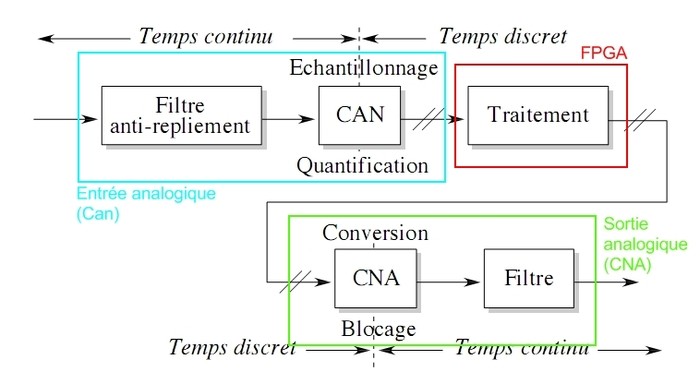
Un petit schéma peut être plus clair :
Les deux filtres sont des filtres passe bas, le premier pour borner le signal le deuxième pour faire l'interpolation.
2003587.jpeg

Citation :
Au final, on revient sur la fréquence de la session, donc sur les "même" échantillons (atténué pour certains) que ce avant le traitement ?

Oui, c'est ça.

[ Dernière édition du message le 22/10/2017 à 11:55:31 ]

14
le problème vient plutôt du placement des échantillons non ?, on peut louper les amplitudes max, shannon c'est ok mais ça reste dans le domaine fréquentiel.

On imagine un signal continue sur une intervalle de temps t=2s, ici on prends 3 échantillons ( je sais c'est très peu ^^),
il est possible de prendre 3 échantillons de valeur < n et pourtant d'avoir dans le signal continue une valeur dépassant n, et donc de perdre dans l’échantillonnage des valeurs d'amplitude dépassant les échantillons.
(ici j'extrapole a un signal passant de conversion en conversion mais le problème est le même pour un signal synthétisé numériquement )

-Ce que je voulais savoir: c'est donc déjà pourquoi les valeurs d'amplitude manquante étaient retrouvé (d'ou l'utilité d'un limiteur TP) --> c'est pendant donc la CNA (a cause du lissage et peut être d'autre facteurs ? )

-Ce que je pense avoir compris:
Il existe un type d'interpolation, qui correspond a un algorithme visant a reproduire la fonction de transfère pendant la CNA.
On utilise donc cet algorithme dans le cadre de la mesure True Peak (numérique), afin de savoir a quelque dixième de dB près les amplitude max du signal post conversion numérique analogique.

--> Je dis ça pour que l'on situe bien le problème évoqué sur le topic !

Je tiens a informer que mon niveau en physique est très proche du niveau du bac, je rame un peu sur pas mal de notion trop théorique..


15
" la fonction sinus cardinal permet la synthèse exacte des signaux à spectre de support fini (formule de Shannon)"
cette fonction permet donc de synthétiser mathématiquement ce qu'il ce passe pendant la CNA, représentation de l'action des filtres pendant la conversion ?
On utilise la même fonction pour sur-échantillonné le signal numérique lors de la mesure True peak numérique ?
c'est bien ça ?
16
Oui c'est tout a fait ça.
Citation :
On utilise donc cet algorithme dans le cadre de la mesure True Peak (numérique), afin de savoir a quelque dixième de dB près les amplitude max du signal post conversion numérique analogique.

Oui, après les développeurs de plug'in peuvent implémenter les choses de différentes manières.
Par exemple le Limiter N6 de Vlag Sound indique dans son manuel (p19), que le plug peut utiliser deux méthodes d'interpolation : une interpolation polynomial et une avec des sinus cardinal.

-La première donne un résultat faux (mais pas trop) et est rapide à calculer. Faux dans le sens ou en interpolant avec un polynôme on obtient pas exactement le signal de départ.
-La deuxième donne un résultat juste mais demande plus de puissance de calcul. Juste dans le sens ou en interpolant avec les sinus cardinal on obtient exactement le signal de départ.

Dans les deux cas on a malgré tout qu'une approximation car on sur-échantillonne "que" d'un facteur 4, 8, ... mais pas infini.

Citation :
cette fonction permet donc de synthétiser mathématiquement ce qu'il ce passe pendant la CNA, représentation de l'action des filtres pendant la conversion ?

Oui, bon en réalité il faudrait tourner la phrase dans l'autre sens : pour faire la CNA on tente de reproduire au mieux ce qu'on a imaginé mathématiquement.

[ Dernière édition du message le 22/10/2017 à 14:56:28 ]

17

Citation de Danbei

Oui, bon en réalité il faudrait tourner la phrase dans l'autre sens : pour faire la CNA on tente de reproduire au mieux ce qu'on a imaginé mathématiquement.

 C'est tout à fait vrai. Mais comme on a commencé par faire des CNA, puis des afficheurs et limiteurs TP, ça revient à discuter de la poule et de l'oeuf icon_mdr.gif

18
Citation :
cette fonction permet donc de synthétiser mathématiquement ce qu'il ce passe pendant la CNA, représentation de l'action des filtres pendant la conversion ?
On utilise la même fonction pour sur-échantillonné le signal numérique lors de la mesure True peak numérique ?
c'est bien ça ?
Oui, c'est une façon correcte de voir les chose.

Pour la petite histoire, il y a des convertisseurs qui procédent en deux étapes :
- D'abord un sur-échantillonnage avec l'interpolation par un sinus cardinal, ce qui revient à applique un filtre passe-bas avec une raideur importante que l'on ne peut pas atteindre avec un filtre analogique ;
- Ensuite un filtrage par un filtre analogique qui n'a pas besoin d'être très raide puisque le filtre numérique a été appliqué avant.

L'idée est de tirer le meilleur parti des deux mondes tout en relâchant les contraintes de conception : La performance de l'ensemble est très bonne alors que les performances des deux briques numérique et analogique restent modestes.

Citation :
le problème vient plutôt du placement des échantillons non ?, on peut louper les amplitudes max, shannon c'est ok mais ça reste dans le domaine fréquentiel.
Tout ce qui se passe dans les fréquences a un corollaire dans le domaine temporel, et inversement.
L'interpolation par le sinus cardinal va faire réapparaître les pics que l'on retrouve en continue... Modulo le risque d'en laisser passer si l'on ne sur-échantillonne pas assez haut.

Ceci étant dit, avec un sur-échantillonnage x4, par exemple, le risque est très (très) faible, d'autant plus qu'un limiteur qui travaille en permanence ce n'est pas très bon signe d'un point de vue de la dynamique et de la musicalité du morceau.
19
Merci pour les réponses ! j'y vois de suite plus clair.
Je vais bosser un peu sur les filtres d'on vous parlez pour faire la conversion, je penses qu'avec cette notion en tête je pourrais bien comprendre le tous dans ça globalité !

20
Je repose ma question des fois que !
Si quelqu'un trouve une doc technique sur la conception du limiteur V3 Oxford, cela m'intéresse !