Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
Notifications
< Retour vers Techniques du Son
Agrandir
Techniques du Son
Forums thématiques
Techniques du Son
Actu 608 608
Articles 632 632
Médias 4 983 5k
Tutoriels Tutos 93 93
Forums 17 055 17,1k

Sujet TIPE

  • 37 réponses
  • 8 participants
  • 11 235 vues
  • 9 followers
Sujet de la discussion Sujet TIPE
Bonjour, j'aurai besoin de conseils pour mon sujet de TIPE j'ai choisis de m'attaquer à la synthèse numérique, et je souhaite faire une application sur le piano et les clavier numérique.
Pour mon expérience j'aimerais essayer de recréer la gamme majeure et la comparé à celle de mon clavier numérique. Qu'en pensez-vous et est-ce réalisable en sachant que j'ai tout de même des connaissances en élec et du matos.
Merci
Afficher le sujet de la discussion
21
Désolé d'avoir mis au temps de temps à répondre mais avec la reprise des cours je n'ai pas eu beacoup de temps, donc en tout cas merci beaucoup et en particulier à EraTom je suis entièrement d'accord avec ce que tu as dit (je me doutais bien que j'assimilais 2 choses qui n'avait rien à voir).
Alors j'ai commencé par mes documentés sur la théorie des signaux, transformée en Z et lien avec Laplace,...
Alors par contre je n'ai pas compris ce que tu veux dire par
Citation :
Comme application, tu peux reprendre la théorie du filtrage en numérique, évoquer le problème de warping des fréquences, etc.

Application théorique ou pratique ?
Quand tu dis filtrage numérique c'est donc tout ce qui est fonction de transfert?
22
Citation :
Quand tu dis filtrage numérique c'est donc tout ce qui est fonction de transfert?
Je parles de l'application d'un filtre (linéaire) que l'on peut effectivement représenter comme une fonction transfert qui pour un signal d'entrée donne un signal de sortie.
Je suis désolé mais je ne me souviens plus si ce que j'évoque est au programme de prépa où si je l'ai vu plus tard...
Le passage au numérique n'est pas aussi trivial qu'on pourrait le penser ; pour la simple élaboration d'un filtre fréquentiel (le b.a.-ba du traitement du signal) on rencontre déjà des "petites" tracasseries.

Citation :
Application théorique ou pratique ?
Les deux ! :)
Le top c'est de réussir à montrer comment guider où consolider la pratique grâce à une étude théorique ; je t'assure alors que ton jury de TIPE aura au minium une demi-molle.

Je vais essayer de te donner (grossièrement) un exemple où l'étude théorique des transformées de Laplace et en Z et d'une approximation permet de guider la conception d'un filtre fréquentiel numérique.
La conception d'un filtre s'appelle aussi, pompeusement, la "synthèse de filtre" (rien à voir avec les synthétiseurs :P). Ça revient "bêtement" à déterminer les coefficients de la transformée de la fonction de transfert associée au filtre.


Lorsque l'on veut réaliser le filtrage d'un signal on commence par donner un gabarit de filtre. Ça ressemble à ceci pour un filtre passe-bas :
1932920.gif

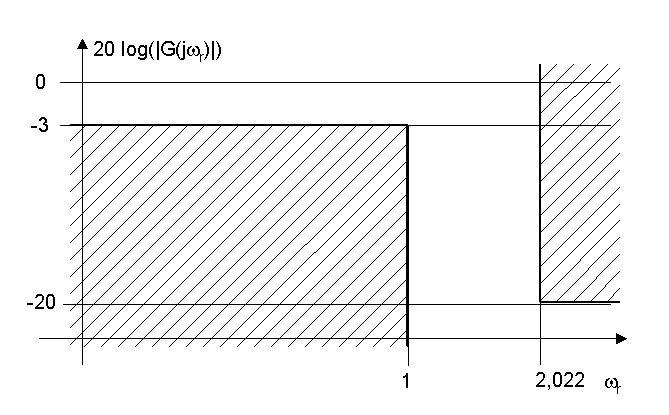
Ça joue un peu le rôle des tolérances de côte et de géométrie sur les pièces en mécanique. Ce gabarit est important parce que le "filtre idéal" n'existe pas. En revanche, il y a un contexte technique qui nous permet de déterminer les contraintes et les libertés possibles du "tracé" du filtre (un peu comme lorsque l'on décide le niveau de planéité d'une surface usinée).

Les parties hachurées sont "interdites" ; ici on veut un filtre qui présente un gain qui peut être compris entre 0dB et -3dB dans la bande passante (il peut partir de 0dB puis descendre de façon monotone jusqu'à -3dB, ou il peut même osciller), la raideur de la pente de coupure est donnée par le couloir vertical entre les zones hachurées, etc.
A partir de ces info on sait déterminer l'ordre minimal du filtre... Et les valeurs de ses coefficients.

Pour les filtres continus ("analogiques") à réponses impulsionnelles infinies il existe toute une littérature pour parvenir à déterminer les coefficients de la transformée de Laplace de la fonction de transfert du filtre.

C'est expliqué en partie ici :
http://f2ea.free.fr/files/cours/filtreActif/1_demarche.html

Et ici tu trouves 2 familles de polynômes utilisées en synthèse de filtre (si tu te demandais à quoi peuvent bien servir les polynômes de Tchebychev... En voici une application) :
http://www.groupes.polymtl.ca/ele2700/Documents/synthese_filtresTC.pdf

Pour résumer l'approche de façon triviale :
- On dessine le gabarit du filtre qui nous irait bien,
- On choisit une famille de polynômes qui détermine "la gueule" de la fonction de transfert du filtre (par exemple si l'on ne veut aucune oscillation du gain dans les bandes atténuée et passante alors c'est un machin de butterworth que l'on choisit),
- On détermine l'ordre du filtre (=le degré du polynôme) et ses coefficients pour qu'il rentre dans notre gabarit.


Pour un filtre numérique (discret, non continu), il y a une difficulté supplémentaire. La transformée en Z qui est le corolaire discret de la transformée de Laplace transforme le plan de l'espace de Laplace en un disque dans l'espace discret...
Pour le dire plus mieux mathématiquement :
Connaissant la transformée de Laplace d'une fonction à temps continue X(p), la transformée en Z de la fonction discrétisée est X(z) en prenant les z = exp(p.Te) où Te est la période d'échantillonnage, l'inverse de la fréquence d'échantillonnage.
(Je pense que tu peux trouver ce résultat et la démo sur n'importe quel cours au sujet de la transformée en Z ; il faut savoir calculer une intégrale avec une distribution de Dirac : Tu as vu ça en prépa ? Je ne sais plus jusqu'où va le programme de mathsup/spé sur l’intégration au sens de Lebesgue).

p = a+j.w : Quand tu avances dans les pulsations w (fréquences), p évolue sur un axe alors que z décrit sur un cercle.


Réutiliser les outils et les critères du "monde continu" dans le "monde discret" n'est pas automatique à cause de cette simple relation.
Il faut alors ré-exprimer tous les critères de convergence, par exemple (je crois qu'en asservissement tu as peut-être vu des critères de stabilité d'un système linéaire causal en étudiant les pôles de la transformée de Laplace de sa fonction de transfert...).

Il y a quand-même moyen de "bricoler" : Par exemple, connaissant la transformée de Laplace de la fonction de transfert d'un filtre continu, on peut trouver la transformée en z d'un filtre discret s'en approchant avec l'approximation bilinéaire :
http://www-hadoc.lag.ensieg.inpg.fr/hadoc/discret/definit/dtw.htm

C'est une approximation de la dérivation/intégration qui permet de montrer que p ~ (2/Te)*(z-1)/(z+1) quand Te est dans un voisinage de 0 (ou quand Fe = 1/Te est grande).
Dans la pratique, tu prends une fonction de transfert en H(p) et tu n'as plus qu'à remplacer p par son approximation pour obtenir Hd(z) ~ H((2/Te)*(z-1)/(z+1)).

L'intérêt c'est que tu peux réutiliser tous les outils qui existent déjà pour les filtres continus (avec les polynômes de Tchebychev, etc. dont je te parlais) ; il suffit d'ajouter la dernière étape de l'approximation bilinéaire pour trouver le filtre numérique qui rentre dans ton gabarit.
En plus tu peux montrer que l'approximation conserve la stabilité du filtre.

Le défaut qu'il ne faut pas louper est le phénomène de "warping des fréquences" dû à l'approximation :
https://en.wikipedia.org/wiki/Bilinear_transform#Frequency_warping

Grâce à une étude théorique du warping tu vois que ce n'est pas un vrai problème : Il suffit de "tordre" le gabarit de départ en décalant les fréquences de coupure pour contrebalancer le warping et s'assurer que le filtre numérique final correspond à ce que l'on voulait initialement.
Et tu as alors résolu un problème bien pratique.

Si ceci n'avait pas été possible, le numérique n'aurait pas été très intéressant...

[ Dernière édition du message le 13/03/2014 à 02:31:06 ]

23
Tout d'abord merci, par contre je vais profiter de mon week-end pour regarder plus en détail les liens que tu m'as donnée et je reviens vers toi pour les questions.
Par contre je ne fait de SI donc pour moi la transformée de laplace ce n'est pas un outil que je manipule, peut-on s'en sortir en sachant le minimum ou il faut un bon bagage en SI?
Et puis comme quoi ils servent les polynômes de Tchebychev
24
Ben disons que tu serais sans doute plus à l'aise et que ça te demanderait moins de boulot.

Il faudrait que tu saches faire le lien entre les transformées de Laplace, en Z et de Fourier pour comprendre les comportements fréquentiels et ce que je t'ai succinctement présenté ici (il y a moyen de faire ça plus rigoureusement et proprement mathématiquement, mais là j'essaie surtout de te passer les idées).

Surtout, connaître les critères de stabilité d'un système asservi qui s'appuient sur l'étude de la transformée de Laplace de sa fonction de transfert pourrait t'aider à comprendre les critères de stabilité d'un filtre : Mathématiquement c'est la même chose.

Et en math, tu sais calculer une intégrale avec une distribution de Dirac ?
Tu pourrais alors tenter la démo du théorème de Shannon pour un signal déterministe (i.e. pas aléatoire).
25
Alors pour le lien entre les différentes transformés je suis en train de bosser dessus.
Alors oui je sais calculer une intégrale avec une distribution de Dirac, oui effectviement faire une démo du théorème de Shannon semble intéressant mais j'ai trouvé plein de démo particulière certaines utilisant les séries de Fourier avec coef exponentielles (pas de Dirac).
Aurais-tu une idée de démarche particulière pour cette démo?
26
Salut,


Oui en utilisant la transformée de Fourier (pas la décomposition en série). C'est, en gros, un cas particulier de la transformée de Laplace.
https://fr.wikipedia.org/wiki/Transformation_de_Fourier
Pour un signal continu s(t) à valeurs dans |R (une fonction du temps), la transformée de Fourier donne une fonction des fréquences S(f) à valeur dans C (fréquence ou pulsation en rad/s. Tu travailles comme tu veux ; il faut juste faire attention à des termes de normalisation). Le module de S(f) permet d'estimer la puissance spectrale.


Tu trouveras la plupart des fois le nom de "densité spectrale de puissance" (DSP) : En réalité le signal s(t) est représenté par un processus stochastiques (une suite de variables aléatoires indexées par t). C'est de cette façon que l'on peut modéliser correctement les bruits (genre un erreur aléatoire sur une série de mesures) ou même les signaux issus d'un phénomène chaotique (ex : en audio le souffle d'une flûte).
La densité spectrale de puissance doit être définie comme l'espérance mathématique du module de la transformée de Fourier du processus stochastique...
... Je te l'indique pour t'apporter un éclairage mais je te conseille d'éviter le sujet en traitant le cas d'un signal déterministe, sinon tu devras expliquer la différence entre la moyenne d'ensemble, la moyenne temporelle, la stationnarité au sens large d'un signal, l'hypothèse ergodique. Bref, des trucs bien hors programme et qu'il n'est pas si simple de s'approprier.


Bon, ceci étant précisé, l'idée du théorème d'échantillonnage est de comparer la DSP d'un signal continu avec la DSP de son homologue échantillonné :
- Tu te donnes un signal s(t),
- Tu supposes connue sa DSP, ou plutôt sa transformée de Fourier S(f),
- Tu considères se(t) qui est le signal échantillonné construit à partir de s(t) (c'est une distribution, j'y reviens après),
- Tu calcules Se(f) en fonction de S(f), et tu compares.

Je vais noter . la multiplication sur les complexes et * le produit de convolution (et me relire à la fin pour vérifier que je ne me suis pas planté :p)
Je surcharge un peu les notations en précisant l'argument s(t), S(f) pour montrer si l'on est bien dans le domaine temporel ou dans le domaine des fréquences.

Se(t) est le produit (temporel) de S(t) avec un peigne de Dirac ⧢(t); le peigne de Dirac est lui-même la somme d'impulsions de Dirac décalées de plusieurs périodes Te ( = 1/Fe, la période d'échantillonnage) :
⧢(t) = Σ δ(t-n.Te), avec n allant de -∞ à +∞.

A chaque instant t :
se(t) = s(t).⧢(t)

Comme avec Laplace, la transformée de Fourier Se(f) de se(t) est le produit de convolution des transformées de s(t) et de ⧢(t) :
Se(f) = S(f)*⧢(f)

Reste à calculer la transformée de Fourier ⧢(t) :
⧢(f) = ∫ ⧢(t).exp(-i.f.t).dt = ∫ Σ δ(t-n.Te).exp(-i.f.t).dt =...
... = Σ ∫ δ(t-n.Te).exp(-i.f.t).dt

Et ∫ δ(t-n.Te).exp(-i.f.t).dt = exp(-i.n.f/Fe)
⇒ ⧢(f) = Σ δ(f-n.Fe)
Un autre peigne de Dirac. Ce n'est pas le résultat le plus simple à établir mais je préfère te laisser chercher pour t'en convaincre (en même temps, avec une recherche Google tu devrais trouver ça tout fait).

⇒ Se(f) = S(f)*⧢(f) = Σ S(f)*δ(f-n.Fe) = Σ ∫ S(f-w).δ(w-n.Fe).dw = Σ S(f-n.Fe)


Et voilà, tu obtiens que Se(f) est la sommes des S(f) translatés de n.Fe.

Ceci implique le problème du repliement spectrale : Dès que la largeur de S(f) (i.e. l'intervalle de f où S(f) est non nulle ; la bande de fréquences qui contient s(t)) dépasse Fe alors les translations successives et la somme créent des zones où les S(f-n.Fe) se recouvrent dans Se(f).
Il est alors impossible de récupérer S(f) (et donc s(t)) à partir de Se(f) (et donc de se(t)).

Si la largeur de S(f) est inférieure à Fe, alors il suffit de récupérer le contenu de la bande qui nous intéresse dans Se(f) pour reconstruire s(t) à partir de se(t) sans perte d'information.
Le "il suffit" est un peu léger : En vérité le filtre parfait, en forme de porte, n'est pas réalisable dans la pratique. Il a toujours des problèmes au bord de la bande à cause du filtre qui ne peut pas être infiniment "raide".
Le problème est contourné en échantillonnant à une fréquence un peu supérieure à ce qui est nécessaire pour restituer la bande utile.

Un autre truc qui n'est pas anodin : Un signal réel donne une transformée de Fourier "symétrique". S'il y a du contenu à une fréquence f alors il y du contenu à la fréquence -f (si ça ne te saute pas au yeux regarde tout simplement ce qu'il se passe avec la transformée d'un sinus, ou alors regarde la transformée inverse).
Du coup un enregistrement audio qui couvre une bande de 0 à F donne en réalité une transformée de Fourier de largeur 2.F allant de -F à F ⇒ Il faut que Fe = 2.F minimum.

Mais ce n'est pas la fréquence la plus élevée qu'il faut regarder car c'est bien la largeur de la bande qui compte.
Une bande allant de F à 2.F peut être échantillonnée à Fe = 2*(2.F-F)) = 2.F sans recouvrement et restituée correctement : Il faut que le filtre qui récupère le signal continu choisisse la bonne bande.

[ Dernière édition du message le 18/03/2014 à 09:43:26 ]

27
x
Hors sujet :
Va bientôt falloir demander aux admins d'installer https://www.mathjax.org/ sur audiofanzine ;-)

beulogue !

28
x
Hors sujet :
Je n'aurais plus qu'à apprendre à m'en servir... ouch
29
Désolé de répondre si tardivement mais avec l'arrivée prochaine des concours ce n'est pas facile.
Tout d'abord merci infiniment EraTom et j'en profite car j'ai quelques questions à te poser.
Pourquoi a-t-on introduit les gabarits, je crois si je ne me trompe que c'est lié au fait que le filtre idéal n'existant pas, on peut le représenter dans le domaine fréquentiel par une fonction porte et si on effectue sa transformer inverse de Fourier on obtient le sinus cardinal qui montre bien que ce n'est pas une fonction causal et donc il nous faut une autre représentation, d'où les gabarits?
Autre chose on constate que les filtres de Butterworth offre l'avantage d'avoir une fréquence de coupure à -3 dB et ce peut importe le degré mais concrètement qu'est-ce que ça représente comme avantage par rapport à un filtre de Tchebycheff? Et aussi tu me rappelles que les filtres de T oscillent dans la bande passante et atténué mais même question j'ai du mal à percevoir ce que c'est physiquement.
Pour le filtrage numérique, approximation D/I, Tustin,... je vais m'y lancer donc pas grand chose à dire dessus.
En ce qui concerne la démo de Dirac je dirais que c'est du tout bon car tu me la vraiment très bien expliqué en détail.
Merci
30
Salut,

Ne t'en fais pas, je me rappelle très bien du "temps libre" dont je disposais en prépa...

Le problème n'est pas la causalité (tu peux toujours placer des retards pour décaler le signal et "remonter le temps"). Le problème vient plutôt du nombre de coefficients du filtre : La porte idéale présente une pente infinie à la fréquence de coupure qui demande un nombre infini de coefficients. L'enveloppe du sinus cardinal va décroissante mais ne sera jamais nulle or dans la pratique on ne peut bien sûr pas réaliser un filtre avec une infinité de coefficients (pour chaque échantillon il faudrait calculer une infinité de sommes / produits.

En tronquant la réponse impulsionnelle (le fenêtrage) pour garder les N premiers coefficients on s'écarte fatalement du filtre idéal en porte.


Idem pour la synthèse des filtres à réponse impulsionnelle infinie : La pente du filtre à la coupure dépend directement du degré du polynôme au dénominateur de sa transformée (de Laplace ou en Z, c'est vrai dans les deux cas). Pour une pente infinie il faut un ordre infini.
On peut montrer que pour un nombre identique de coefficient un filtre RII sera plus proche de la porte qu'un filtre RIF... mais plus l'ordre est grand plus il y a de pôles et plus il y a de risque de problème de stabilité.


Tout ça pour dire qu'il n'y a pas de solution miracle. Bien souvent le "meilleur filtre" sera celui qui répond au besoin de l'application en présentant le plus petit nombre de coefficients (en assurant la stabilité).
C'est alors que le gabarit du filtre permet de résumer les caractéristiques clefs liées à l'application.

Par exemple pour l'audio, si l'on veut échantillonner dans le but de mettre le signal sur un CD :
- Notre oreille est sourde dès 20kHz ; la bande qui nous intéresse se trouve entre 0Hz et 20kHz ;
- Le CD permet de graver un signal échantillonné @44kHz et donc de représenter une bande allant de 0 à 22kHz.

Ce qui donne pour le filtre anti-recouvrement :
- De 0Hz à 20kHz il faudrait qu'il ne modifie pas le signal parce que c'est la bande que l'on va écouter;
- Pour tout ce qui est au-dessus de 22kHz il faut qu'il atténue sévèrement pour qu'il n'y ait pas de repliement.
- Entre 20kHz et 22kHz... Le filtre fait comme il veut, on s'en moque.

En traduisant ceci dans un gabarit de filtre :
- Pour la partie allant de 0 à 20kHz on veut une réponse "la plus plate possible" pour ne pas modifier le contenu spectrale de la bande d'intérêt : On ne veut pas booster les basses ou les aigus et on cherche le filtrage "le plus neutre possible"). En clair, de 0 à 20kHz on veut un filtre dont le gain colle 0dB.
- Pour tout ce qu'il y a au-delà de 22kHz on veut qu'il atténue d'au moins... disons 100dB. S'il atténue d'avantage tant mieux, mais il faut qu'il ait un gain maximum de -100dB
- De 20kHz à 22kHz c'est la transition entre la bande passante et la bande atténuée ; nous n'avons pas besoin que le filtre soit plus raide que ça.

x
Hors sujet :
Mine de rien, je viens de te faire une mini "analyse du besoin" "spécification technique" "déclinaison d'exigence" qui est un processus important du travail d'ingénieur... trop souvent bâclé et qui finit par mener des projets dans le mur.
C'est du "management" et de la qualité ; des trucs qui ne passionnent pas vraiment les ingé car loin de la technique pourtant, d'après mon expérience, 9/10 ce n'est pas à cause d'un problème technique qu'un projet capote mais plutôt parce que la déclinaison des fonctions techniques n'a pas été faite correctement.
https://fr.wikipedia.org/wiki/Analyse_fonctionnelle_%28conception%29
https://fr.wikipedia.org/wiki/Exigence_%28ing%C3%A9nierie%29


Citation :
les filtres de Butterworth offre l'avantage d'avoir une fréquence de coupure à -3 dB et ce peut importe le degré mais concrètement qu'est-ce que ça représente comme avantage
Ce n'est pas un "avantage", c'est simplement une caractéristique parmi d'autres.
Le gros avantage du filtre de Butterworth est que c'est le filtre qui présente la réponse la plus plate possible dans la bande passante.

Regarde ces graphiques :
https://commons.wikimedia.org/wiki/File:Electronic_linear_filters.svg

Ils présentent les réponses fréquentielles des 4 types de filtres RII possibles pour un ordre donné (ils ont tous le même nombre de coefficients) qui coupent à la moitié de la bande.

Avec le gabarit que je t'ai donné pour le CD, les choix possibles sont le filtre de Butterworth ou le filtre de Tchebychev 2.
Les deux autres sont à écarter car ils ne sont pas plats dans la bande utile alors que c'est un point souhaité.

Entre Butterworth ou le filtre de Tchebychev 2 il faudrait avoir un critère plus fin pour savoir ce qui importe le plus entre la raideur plus importante du filtre de Tchebychev et la réponse plate du Butterworth.


Pour la petite histoire, j'avais travaillé sur un projet audio bas-coût où l'enregistrement était pourri. Le signal était numérisé ; avant l'enregistrement il subissait systématiquement une correction tonale : En clair il passait dans un EQ.
J'ai viré le filtre d'anti-recouvrement pour mettre un filtre elliptique à la place dont les oscillations dans la bande utile correspondaient à la correction de l'EQ.
Comme le filtre elliptique est particulièrement raide, j'ai pu réduire son ordre et rentrer dans le gabarit de coupure : Filtre d'anti-recouvrement plus simple (moins de coefficients), EQ devenu inutile (et donc retiré) juste en ajustant le gabarit au besoin réel...