Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
FR
EN
Notifications
  • Refonte graphique octobre 2025
    Refonte graphique octobre 2025
    Une refonte graphique vient d'être mise en ligne. Nous espérons qu'elle vous plaira. Merci de nous signaler tout bug ou perte de fonctionnalité ici →
  • Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Pour célébrer notre quart de siècle, UVI se joint à nous et vous offre le Digital Synsations Vol.1. Pour en profiter c'est par ici 👉
  • Nouveauté : Bookmark article, news ou tuto
    Nouveauté : Bookmark article, news ou tuto
    Bookmarkez un article, une news ou un tuto et retrouvez-le dans votre section "Mes signets" du menu membre.
  • 6 nouveaux annuaires
    6 nouveaux annuaires
    Luthiers, Réparateurs, Cours de musique, Studios d’enregistrement, de mastering et de répétition... Suggérez l’ajout d’une entreprise, inscrivez la vôtre ou déposez un avis.
  • Alertes disponibilité et baisse de prix
    Alertes disponibilité et baisse de prix
    Ces nouvelles fonctionnalités vous permettent d'être informé·e dès qu'un produit est disponible ou que son prix a baissé.
  • Tentatives d'arnaque dans les petites annonces
    Nous faisons face depuis quelques mois à une recrudescence de tentatives d'arnaques dans les petites annonces. Suivez nos recommandations >
Techniques du Son
News
Articles
Médias
Forums
Tutoriels Tutos

Sujet TIPE

  • 37 réponses
  • 8 participants
  • 12 081 vues
  • 9 followers
Sujet de la discussion Sujet TIPE
Bonjour, j'aurai besoin de conseils pour mon sujet de TIPE j'ai choisis de m'attaquer à la synthèse numérique, et je souhaite faire une application sur le piano et les clavier numérique.
Pour mon expérience j'aimerais essayer de recréer la gamme majeure et la comparé à celle de mon clavier numérique. Qu'en pensez-vous et est-ce réalisable en sachant que j'ai tout de même des connaissances en élec et du matos.
Merci
2

Hello, 

Si je comprends bien, ton sujet porte sur la modélisation d'un son de piano et/ou de sons synthétiques ? "Clavier numérique", c'est assez vague...

Ce que je ne comprends pas c'est le rapport entre ce qui précède et la gamme majeure...

Quelle est la finalité exacte de ces travaux ? Que souhaites-tu prouver ou mettre en avant ? Quand tu dis "je souhaite faire une application", c'est-à-dire un programme ? Ou bien est-ce comme dans "mettre en application" ?

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
3
Pareil que a.k.a, j'ai l'impression que déjà ce n'est pas très clair dans ta tête vu que je ne comprend pas du tout où tu veux en venir… Il faut que tu nous décrive en détail ce que tu as l'intention de faire.

C'est quoi un TIPE ? Un genre de TPE comme en terminale j'imagine ?

"Recréer la gamme majeure", ça ne veut pas dire grand-chose. La musique occidentale est basée sur la gamme tempérée (=tous les demi-tons sont égaux). Entre deux octaves on a 12 demi-tons, et une octave correspond à un doublement de la fréquence. On a donc une suite géométrique de raison racine douzième de 2 (pour obtenir le demi-ton suivant une note, on multiple sa fréquence par la racine douzième de deux, soit ~1,059).

La gamme majeure c'est 1 ton - 1 ton - 1/2 ton - 1 ton - 1 ton - 1 ton - 1/2 ton. Voilà comment on obtient les fréquences des notes. Si c'est juste ça, ça prend 30 secondes avec un tableur.

Après, la synthèse sonore est un vaste sujet, il existe différentes méthodes. Dans tous les cas ça me paraît bien trop long et compliqué à mettre en œuvre dans le cadre d'un TPE. Tu as quoi comme niveau en traitement du signal (notamment numérique), en programmation et en électronique ? Et est-ce-que tu maîtrises le logiciel Matlab (ça peut servir) ?

A la limite tu pourrais essayer de faire un synthé avec un arduino et le contrôler avec un clavier MIDI, ça pourrait être intéressant pédagogiquement et réalisable. Mais ne t'attends pas à recréer le son d'un piano !

Si je comprend bien, tu veux faire un synthé logiciel ? tu le contrôlera comment ?
Et quand tu dis que tu as du matos, qu'entends-tu par là (ordinateur, fer à souder, GBF, synthé, tractopelle…) ?
4

Oui, TIPE = TPE.

En gros, +1 avec toi, Shreddator, il faut plus d'infos sur ton projet si tu veux de l'aide. bravo

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
5
Le TIPE c'est un TPE mais en maths sup / spé. Le thème de cette année est "transfert, échange" : Comment le relies-tu à la synthèse du son d'un instrument ?

Le "hors sujet" est très sévèrement sanctionné par certains jurys...

[ Dernière édition du message le 01/03/2014 à 00:06:16 ]

6

Ah, il aurait fallu commencer par là. bravo

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
7
ah, je suis bien content d'avoir quitté la prépa! "Transfert, échange", pour moi ça sonnait thermo et vu la haine que j'ai envers cette discipline j'avais peu envie de faire un TIPE de thermo...
Pour "transfert", selon le contenu de ton tipe (en effet c'est pas clair) tu peux axer sur les fonctions de transfert par exemple. Pour "échange", c'est moins évident à priori.
8
Alors merci pour vos réponses et je vais tenter d'être plus clair.
Alors disons qu'on peut rapprocher le TIPE du TPE mais avec un niveau supérieure et de la théorie sachant que je suis MP on attend tout de même un peu de physique.
Alors quand j'ai dit que j'avais du matos c'est une carte arduino, fer à souder, des A.O et j'ai à ma disposition le labo du lycée
J'ai aussi matlab mais je viens de débuter dessus donc il ne faudra pas s'attendre à des applications poussés, tout du moins pour l'instant.
Alors mon projet en détail est le suivant: La synthèse sonore et le cas particulier du piano.
Mes problématiques sont: Qu'est-ce que le procédé de synthèse sonore? Comment ça marche? Comment synthétiser le son d'un piano?
Ma première partie est une généralité sur la synthèse sonore, avec les différents procédés, son théorème fondamental, les perturbations qui peuvent intervenir et un peu d'optimisation de synthèse en abordant le suréchantillonnage. Je pensais essayer d'illustrer tout ça avec Matlab (échantillonnage, repliement , quantification, filtre, convolution.
Venant en à la deuxième partie, je souhaitait faire un petit montage (CAN) et synthétisé le son d'un piano, une gamme finalement ça ne sert à rien déjà une note serait pas mal.
Ma dernière partie qui est floue est concentré sur un modèle particulier de synthèse sonore qui correspond au piano et là 2 choix s'offre à mon soit une modélisation physique (avec la théorie des cordes )qui me semble assez complexe ou sinon la synthèse par modulation de fréquence.
Ce qu'il faut savoir c'est que tout ça doit tenir en 10 minutes précise d'exposé et qu'il n'y a pas de dossier à rendre.
J'ai vu que Shreddator parle d'une utilisation d'arduino (que j'ai déjà utilisé pour mon tpe et ppe donc j'ai des connaissances et je le maitrise à peu près) mais est-elle en lien avec sujet?
Quel est le lien entre transfert et échange et mon sujet, il me semble que le principe de conversion correspond bien à un transfert.
Voilà donc si vous pouviez me donner votre avis et m'orienter vers des pistes.
Merci
9
Citation de soulkira :
Venant en à la deuxième partie, je souhaitait faire un petit montage (CAN) et synthétisé le son d'un piano, une gamme finalement ça ne sert à rien déjà une note serait pas mal.
Ma dernière partie qui est floue est concentré sur un modèle particulier de synthèse sonore qui correspond au piano et là 2 choix s'offre à mon soit une modélisation physique (avec la théorie des cordes )qui me semble assez complexe ou sinon la synthèse par modulation de fréquence.


Oula, la théorie des cordes c'est pas trop le sujet (la théorie des cordes c'est de la physique subatomique).
J'imagine que tu veux parler de mécanique : la corde du piano serait alors assimilée à un câble tendu. Vous faites des vibrations de systèmes continus en prépa ? De la RDM ? En gros en faisant ça tu va pouvoir calculer analytiquement les modes propres du câble tendu (de la corde), ce qui est d'un intérêt limité.
La sonorité du piano est bien plus compliquée que ça, c'est influencé par les modes propres de tous les éléments qui le composent, il y a des amortissements qui interviennent un peu partout, la forme de la sollicitation par les marteaux, etc…
En faire un modélisation serait extrêmement complexe (ça pourrait faire un sujet de thèse peut-être).

Sinon la synthèse FM est assez aléatoire dans les résultats, s'approcher un son de piano est sans doute possible, mais y arriver par une démarche rationnelle risque d'être difficile. En général ça fonctionne plutôt en essayant plein de choses jusqu'à ce qu'on arrive au résultat attendu.

A ta place je m'orienterais vers de la synthèse additive si ton but est de recréer un son artificiellement. Mais l'Arduino ne sera pas assez puissant pour ça, il faudrait un PC ou un DSP.

Sinon quand tu parles de suréchantillonnage, de fabriquer un convertisseur, etc, c'est hors-sujet donc évite de t'éparpiller…

[ Dernière édition du message le 01/03/2014 à 16:10:54 ]

10
Alors effectivement c'est un sujet de thèse qui revient souvent (à polytechnique).
En fait j'ai trouvé ça sur le sujet de modèle mécanique http://www.lma.cnrs-mrs.fr/~kronland/article_REE.pdf et je comptais le travailler avec mon prof mais il y a effectivement la synthèse additive mais serait-il possible d'en faire une application directe?
Pour le suréchantillonnage je l'aborde avec ces différentes méthodes et oui je pensais faire un convertisseur (qui correspond à ma deuxième partie expérience) et échantillonner le son d'un piano
11

Ok, pour TIPE, my bad, t'es pas un lycéen, enfin, plus tout à fait. icon_biggrin.gif

 

Citation :

La sonorité du piano est bien plus compliquée que ça, c'est influencé par les modes propres de tous les éléments qui le composent, il y a des amortissements qui interviennent un peu partout, la forme de la sollicitation par les marteaux, etc…
En faire un modélisation serait extrêmement complexe (ça pourrait faire un sujet de thèse peut-être).

D'accord avec ça, sans parler de la table d'harmonie, des résonances engendrées par la structure de ladite table, etc. Oui, des sujets de thèse sur la modélisation physique, y en a dans un tas d'écoles et d'institutions...

Effectivement, ça risque d'être un peu short pour matlab.

Citation :

serait-il possible d'en faire une application directe?

Il existe des synthés à modélisation physique. Tu voudrais contrôler avec l'arduino une émulation de piano que tu aurais faite toi-même, c'est ça ?

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
12
Pour l'application directe je parlais de la synthèse additive, après faire une manip avec arduino pourquoi pas mais vu que c'est de l'oral arduino risque d'être assez limité car il est intéressant dans le cas ou on montre notre création.
13

Qu'entends-tu précisément par "faire une application directe de la synthèse additive" ?

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
14
Réaliser une petite manip sur la synthèse additive (à l'oscillo par exemple)
15

Pour démontrer quoi ? Développe un peu...

À l'oscillo, qu'entends-tu par là, tu voudrais trifouiller un oscillo pour montrer à ton jury...quoi ?

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
16
Bon... Je ne cherche pas à te défoncer mais tu m'inquiètes un peu parce que j'ai l'impression que tu vas te lancer dans un truc à côté de la plaque.


Tu confonds la théorie de l'échantillonnage (et le procédé de discrétisation) avec la problématique de la synthèse sonore (i.e. la création d'un son de manière "artificielle", ou plutôt par traitement mathématique sans enregistrement et prise de son de phénomènes mécaniques).


Citation :
Quel est le lien entre transfert et échange et mon sujet, il me semble que le principe de conversion correspond bien à un transfert.
Ça me semble capilotracté d'autant plus que le thème principal de ton exposé semble être le procédé de synthèse lui-même (et pas les conversions numérique-analogique).

Citation :
Ma première partie est une généralité sur la synthèse sonore, avec les différents procédés, son théorème fondamental
Le théorème fondamental de la synthèse sonore... ?

Citation :
un peu d'optimisation de synthèse en abordant le suréchantillonnage
Ah, ok... donc en fait tu assimiles bien la synthèse sonore à l'échantillonnage et au traitement numérique.
Ce que l'on appelle la "synthèses sonore" peut-être réalisée avec des techniques analogiques qui ne font pas intervenir de signaux discrétisés.
https://upload.wikimedia.org/wikipedia/commons/e/e6/Moog_Modular_55_img2.jpg

Le suréchantillonnage n'est pas une "optimisation" mais une technique déployée dans différents cadres...
("L'optimisation" fait référence à une autre classes de problèmes mathématique, que l'on rencontre parfois pour des traitements automatiques en lien avec le traitement du signal).

Citation :
Ma dernière partie qui est floue est concentré sur un modèle particulier de synthèse sonore qui correspond au piano
Ta première partie l'est encore pour l'instant...


Je te conseille de laisser tomber la partie "synthèse sonore" et l'application du piano car tu t'embrouilles visiblement dans les concepts et tu t'écartes du sujet initial. Ce n'est pas un reproche : Tu t'attaques à un sujet plus complexe qu'il n'y parait au premier abord.

Documente-toi sur la théorie du signal et comprends bien le processus de discrétisation (quantification / échantillonnage).
Tu peux tenter une démonstration simplifiée du théorème de Shannon (i.e. comparer la transformée de Fourier d'un signal continu avec sa version "multipliée par un peigne de Dirac" qui modélise l'effet de l'échantillonnage).

Les effets de la quantification font nécessairement rentrer des notions de probabilité qui (dans mes souvenirs) ne sont pas abordés en prépa. Si tu rentres dans les concepts de processus stochastiques, etc. j'ai peur que tu te prennes les pieds dans le tapis, mais tu peux toujours y jeter un œil.
(La question de l'échantillonnage peut être abordée sur des signaux "déterministes").

Comme application, tu peux reprendre la théorie du filtrage en numérique, évoquer le problème de warping des fréquences, etc.
Tu peux faire le lien entre les transformées de Fourier / Laplace et la transformée en Z(et comment l'on passe d'un "demi-plan" à un "disque ouvert"). Vaste programme...


La théorie du signal est très "mathématique" mais il s'agit de math appliquées à la physique ; je pense que tu sauras faire des liens assez facilement.
C'est moins "spectaculaire" que la synthèse d'un son de piano mais ce sont les fondements des applications numériques.
Ces quelques points forment déjà un enseignement qui s'étale sur plusieurs années dans le supérieur ; il y a largement de quoi alimenter une présentation de 10 minutes devant un jury.

[ Dernière édition du message le 02/03/2014 à 15:59:18 ]

17
Citation :
En fait j'ai trouvé ça sur le sujet de modèle mécanique http://www.lma.cnrs-mrs.fr/~kronland/article_REE.pdf

Hello,
J'ai parcouru en biais ce document qui a l'air bien intéressant.
Si tu te lances dans la synthèse de piano par le biais de la simulation mécanique, ce document pourra t'être utile :
http://ebookbrowsee.net/32bfe50f470ae2e2e5-pdf-d484709474

[ Dernière édition du message le 02/03/2014 à 19:29:06 ]

18
Je suis complètement d'accord avec ce qu'a dit EraTom, et surtout ça serait plus dans le thème "échanges et transferts".
19
Enfin bon, j'espère ne pas avoir cassé le moral de soulkira...

Si tu as des questions sur des aspects théoriques / mathématique / physique je peux te filer un coup de main.
Je n'ai certainement plus l'agilité que tu dois avoir à manipuler des formules mais je peux t'aider à attaquer certaines démo de théorèmes du traitement du signal, pour les faire partir correctement et aboutir.
20

Je n'espère pas non plus, ce serait dommage, la discussion serait des plus constructives, tu sembles savoir de quoi tu parles. bravo

"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
21
Désolé d'avoir mis au temps de temps à répondre mais avec la reprise des cours je n'ai pas eu beacoup de temps, donc en tout cas merci beaucoup et en particulier à EraTom je suis entièrement d'accord avec ce que tu as dit (je me doutais bien que j'assimilais 2 choses qui n'avait rien à voir).
Alors j'ai commencé par mes documentés sur la théorie des signaux, transformée en Z et lien avec Laplace,...
Alors par contre je n'ai pas compris ce que tu veux dire par
Citation :
Comme application, tu peux reprendre la théorie du filtrage en numérique, évoquer le problème de warping des fréquences, etc.

Application théorique ou pratique ?
Quand tu dis filtrage numérique c'est donc tout ce qui est fonction de transfert?
22
Citation :
Quand tu dis filtrage numérique c'est donc tout ce qui est fonction de transfert?
Je parles de l'application d'un filtre (linéaire) que l'on peut effectivement représenter comme une fonction transfert qui pour un signal d'entrée donne un signal de sortie.
Je suis désolé mais je ne me souviens plus si ce que j'évoque est au programme de prépa où si je l'ai vu plus tard...
Le passage au numérique n'est pas aussi trivial qu'on pourrait le penser ; pour la simple élaboration d'un filtre fréquentiel (le b.a.-ba du traitement du signal) on rencontre déjà des "petites" tracasseries.

Citation :
Application théorique ou pratique ?
Les deux ! :)
Le top c'est de réussir à montrer comment guider où consolider la pratique grâce à une étude théorique ; je t'assure alors que ton jury de TIPE aura au minium une demi-molle.

Je vais essayer de te donner (grossièrement) un exemple où l'étude théorique des transformées de Laplace et en Z et d'une approximation permet de guider la conception d'un filtre fréquentiel numérique.
La conception d'un filtre s'appelle aussi, pompeusement, la "synthèse de filtre" (rien à voir avec les synthétiseurs :P). Ça revient "bêtement" à déterminer les coefficients de la transformée de la fonction de transfert associée au filtre.


Lorsque l'on veut réaliser le filtrage d'un signal on commence par donner un gabarit de filtre. Ça ressemble à ceci pour un filtre passe-bas :
1932920.gif

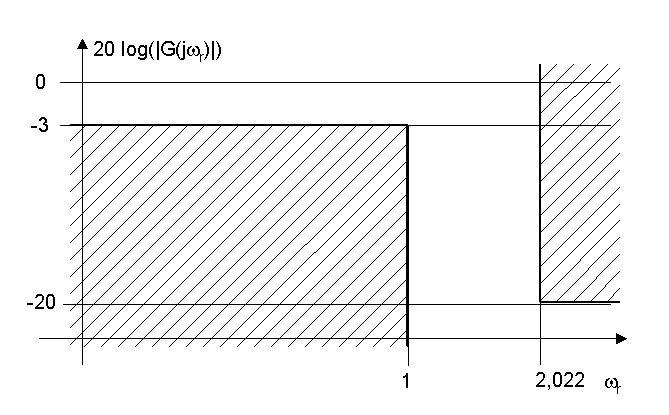
Ça joue un peu le rôle des tolérances de côte et de géométrie sur les pièces en mécanique. Ce gabarit est important parce que le "filtre idéal" n'existe pas. En revanche, il y a un contexte technique qui nous permet de déterminer les contraintes et les libertés possibles du "tracé" du filtre (un peu comme lorsque l'on décide le niveau de planéité d'une surface usinée).

Les parties hachurées sont "interdites" ; ici on veut un filtre qui présente un gain qui peut être compris entre 0dB et -3dB dans la bande passante (il peut partir de 0dB puis descendre de façon monotone jusqu'à -3dB, ou il peut même osciller), la raideur de la pente de coupure est donnée par le couloir vertical entre les zones hachurées, etc.
A partir de ces info on sait déterminer l'ordre minimal du filtre... Et les valeurs de ses coefficients.

Pour les filtres continus ("analogiques") à réponses impulsionnelles infinies il existe toute une littérature pour parvenir à déterminer les coefficients de la transformée de Laplace de la fonction de transfert du filtre.

C'est expliqué en partie ici :
http://f2ea.free.fr/files/cours/filtreActif/1_demarche.html

Et ici tu trouves 2 familles de polynômes utilisées en synthèse de filtre (si tu te demandais à quoi peuvent bien servir les polynômes de Tchebychev... En voici une application) :
http://www.groupes.polymtl.ca/ele2700/Documents/synthese_filtresTC.pdf

Pour résumer l'approche de façon triviale :
- On dessine le gabarit du filtre qui nous irait bien,
- On choisit une famille de polynômes qui détermine "la gueule" de la fonction de transfert du filtre (par exemple si l'on ne veut aucune oscillation du gain dans les bandes atténuée et passante alors c'est un machin de butterworth que l'on choisit),
- On détermine l'ordre du filtre (=le degré du polynôme) et ses coefficients pour qu'il rentre dans notre gabarit.


Pour un filtre numérique (discret, non continu), il y a une difficulté supplémentaire. La transformée en Z qui est le corolaire discret de la transformée de Laplace transforme le plan de l'espace de Laplace en un disque dans l'espace discret...
Pour le dire plus mieux mathématiquement :
Connaissant la transformée de Laplace d'une fonction à temps continue X(p), la transformée en Z de la fonction discrétisée est X(z) en prenant les z = exp(p.Te) où Te est la période d'échantillonnage, l'inverse de la fréquence d'échantillonnage.
(Je pense que tu peux trouver ce résultat et la démo sur n'importe quel cours au sujet de la transformée en Z ; il faut savoir calculer une intégrale avec une distribution de Dirac : Tu as vu ça en prépa ? Je ne sais plus jusqu'où va le programme de mathsup/spé sur l’intégration au sens de Lebesgue).

p = a+j.w : Quand tu avances dans les pulsations w (fréquences), p évolue sur un axe alors que z décrit sur un cercle.


Réutiliser les outils et les critères du "monde continu" dans le "monde discret" n'est pas automatique à cause de cette simple relation.
Il faut alors ré-exprimer tous les critères de convergence, par exemple (je crois qu'en asservissement tu as peut-être vu des critères de stabilité d'un système linéaire causal en étudiant les pôles de la transformée de Laplace de sa fonction de transfert...).

Il y a quand-même moyen de "bricoler" : Par exemple, connaissant la transformée de Laplace de la fonction de transfert d'un filtre continu, on peut trouver la transformée en z d'un filtre discret s'en approchant avec l'approximation bilinéaire :
http://www-hadoc.lag.ensieg.inpg.fr/hadoc/discret/definit/dtw.htm

C'est une approximation de la dérivation/intégration qui permet de montrer que p ~ (2/Te)*(z-1)/(z+1) quand Te est dans un voisinage de 0 (ou quand Fe = 1/Te est grande).
Dans la pratique, tu prends une fonction de transfert en H(p) et tu n'as plus qu'à remplacer p par son approximation pour obtenir Hd(z) ~ H((2/Te)*(z-1)/(z+1)).

L'intérêt c'est que tu peux réutiliser tous les outils qui existent déjà pour les filtres continus (avec les polynômes de Tchebychev, etc. dont je te parlais) ; il suffit d'ajouter la dernière étape de l'approximation bilinéaire pour trouver le filtre numérique qui rentre dans ton gabarit.
En plus tu peux montrer que l'approximation conserve la stabilité du filtre.

Le défaut qu'il ne faut pas louper est le phénomène de "warping des fréquences" dû à l'approximation :
https://en.wikipedia.org/wiki/Bilinear_transform#Frequency_warping

Grâce à une étude théorique du warping tu vois que ce n'est pas un vrai problème : Il suffit de "tordre" le gabarit de départ en décalant les fréquences de coupure pour contrebalancer le warping et s'assurer que le filtre numérique final correspond à ce que l'on voulait initialement.
Et tu as alors résolu un problème bien pratique.

Si ceci n'avait pas été possible, le numérique n'aurait pas été très intéressant...

[ Dernière édition du message le 13/03/2014 à 02:31:06 ]

23
Tout d'abord merci, par contre je vais profiter de mon week-end pour regarder plus en détail les liens que tu m'as donnée et je reviens vers toi pour les questions.
Par contre je ne fait de SI donc pour moi la transformée de laplace ce n'est pas un outil que je manipule, peut-on s'en sortir en sachant le minimum ou il faut un bon bagage en SI?
Et puis comme quoi ils servent les polynômes de Tchebychev
24
Ben disons que tu serais sans doute plus à l'aise et que ça te demanderait moins de boulot.

Il faudrait que tu saches faire le lien entre les transformées de Laplace, en Z et de Fourier pour comprendre les comportements fréquentiels et ce que je t'ai succinctement présenté ici (il y a moyen de faire ça plus rigoureusement et proprement mathématiquement, mais là j'essaie surtout de te passer les idées).

Surtout, connaître les critères de stabilité d'un système asservi qui s'appuient sur l'étude de la transformée de Laplace de sa fonction de transfert pourrait t'aider à comprendre les critères de stabilité d'un filtre : Mathématiquement c'est la même chose.

Et en math, tu sais calculer une intégrale avec une distribution de Dirac ?
Tu pourrais alors tenter la démo du théorème de Shannon pour un signal déterministe (i.e. pas aléatoire).
25
Alors pour le lien entre les différentes transformés je suis en train de bosser dessus.
Alors oui je sais calculer une intégrale avec une distribution de Dirac, oui effectviement faire une démo du théorème de Shannon semble intéressant mais j'ai trouvé plein de démo particulière certaines utilisant les séries de Fourier avec coef exponentielles (pas de Dirac).
Aurais-tu une idée de démarche particulière pour cette démo?