113 réponses
26 participants
16 185 vues
28 followers

newjazz

8742

Je poste, donc je suis

Membre depuis 20 ans

Sujet de la discussion Posté le 16/09/2014 à 16:44:05

Dans le précédent article, nous avons vu que le son était composé d’ondes. Comme beaucoup de choses dans la vie, celles-ci peuvent être simples ou complexes.

Lire l'article

Ce thread a été créé automatiquement suite à la publication d'un article. N'hésitez pas à poster vos commentaires ici !

Accepter qu'on n'sait pas, c'est déjà l'premier pas.

MUSICIENS ET PUBLIC, PROTEGEZ VOS OREILLES!

Afficher le sujet de la discussion

Les Cowboys Etanches

238

Posteur·euse AFfiné·e

Membre depuis 20 ans

51 Posté le 20/09/2014 à 15:35:12

Euh, rendons à Fourier ce qui revient à Fourier. Seule une onde complexe dite "harmonique" peut me semble-t-il être décomposée en une série d'ondes sinusoïdales. Un éternuement c'est plus délicat. L'éternuement constituera toujours un mystère sonore. Non ?

Autant j'aime pas la tarte aux pommes, autant une bonne tarte aux pommes...

https://lescowboysetanches.bandcamp.com/

https://soundcloud.com/les-cowboys-etanches

Anonyme

970

52 Posté le 20/09/2014 à 15:53:59

Citation de trazom :

Pourquoi une onde carrée est-elle beaucoup plus sonore, audible, agressive, qu'une onde sinusoïdale ? La réponse est dans Fourrier. On n'est pas obligé de vouloir comprendre, mais quand on commence à se tourner vers la synthèse, sonore, c'est mieux de comprendre un peu.
Tiens, pourquoi j'ai l'impression qu'il y a un battement ? (Et donc, comment l'éviter ?)
Tiens, c'est bizarre, quand je passe en mono, le son devient tout vide ?
Tiens, c'est bizarre, ces deux sons joués ensemble, ça sonne tout métallique crado. Que faire ?
Tiens, j'ai downpitché de 48 demi-tons, mais mon son manque d'air, pourquoi ?
Tiens, quand je joue ces deux micros ensemble, ça sonne moins que quand il n'y en a qu'un. C'est contradictoire ?
Tiens, je mets un EQ sur mon son sinusoïdal et il ne se passe rien, pourquoi ?
Etc, etc.

Effectivement, si on ne comprend pas qu'un son est constitué d'une somme de sinusoïdes, on ne peut comprendre ce type d'intéractions entre deux signaux :D:

Cela dit, dans des synthés vst, j'avais déjà utilisé des filtres sur des sinus, et ça ne faisait pas que réduire le volume, ça changeait un peu le son... je me demande ce qu'il y a dans leur "sinus"... peut-être qu'ils sont non parfaits (offeset, asymétriques,etc) pour imiter les analo... ?

Citation :

Citation :
Avec cet outil, on peut très bien obtenir le spectre d'un signal complet, y compris le transitoire.

Avec une limite : La résolution du spectre estimée par un périodogramme (&co) d'un signal trop court dans le temps ne permet pas toujours d'extraire une information pertinente.

Bah si je ne me trompe pas, la fréquence la plus basse visible dans un spectre suite à une transformée de Fourier doit correspondre à l'inverse de la durée du signal mesuré (tu ne peux pas avoir de composantes spectrale dont la période serait plus grande que celle de la plus longue sinusoïdale dans ton signal, elle n'est tout simplement pas présente)
Après inversement, tu peux prendre la transformée de Fourier d'un morceau de 5 minutes, tu auras la répartition en fréquence de tout ce qui se trouve dans ce morceau et ça ne voudra pas dire grand chose.
Donc oui, c'est sûr c'est un "bête" calcul, mais il faut savoir ce qu'on fait comme toujours...

[ Dernière édition du message le 20/09/2014 à 16:08:51 ]

hhub17

3115

Squatteur·euse d’AF

Membre depuis 19 ans

53 Posté le 20/09/2014 à 16:11:13

Choc, il marche bien maintenant ton lien, une illustration simple et efficace qui complète et illustre élégamment, à mon sens, certains aspects un peu stratosphériques de cette discussion.

Merci du complément "stratosphérique" à ceux qui savent : il vaut souvent mieux un qui sait que deux qui cherchent , et moi, je cherche encore pas mal.

Be bop a loulou !

miles1981

8370

Je poste, donc je suis

Membre depuis 21 ans

54 Posté le 20/09/2014 à 18:58:32

Citation de Les :

Euh, rendons à Fourier ce qui revient à Fourier. Seule une onde complexe dite "harmonique" peut me semble-t-il être décomposée en une série d'ondes sinusoïdales. Un éternuement c'est plus délicat. L'éternuement constituera toujours un mystère sonore. Non ?

Non. Tout signal peut être décrit comme la somme de sinusoïdes. C'est juste qu'il y aura plus de fréquences qui rentrent en ligne de compte que pour un signal "musical".

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

EraTom

2282

AFicionado·a

Membre depuis 14 ans

55 Posté le 21/09/2014 à 00:45:25

Non, tout signal ne peut pas être décomposé en une somme de sinusoïdes. Seuls les signaux périodiques (ou quasi-périodiques) le peuvent de façon efficace (comme le dit implicitement l'article). Pour un bruit, par exemple, il faut utiliser d'autres outils mathématiques.

Citation :

Bah si je ne me trompe pas, la fréquence la plus basse visible dans un spectre suite à une transformée de Fourier doit correspondre à l'inverse de la durée du signal mesuré

Je ne parlais pas de ça mais de la limite en résolution (i.e. la capacité à discerner deux fréquences distinctes).
Pour obtenir un spectre harmonique avec des composantes bien localisées dans l'espace des fréquences (un spectre avec des pics) il faut que la signal temporel soit d'une durée infinie...
... Et bien sûr dans la pratique c'est impossible.

On utilise donc des trames de durées finies et leurs spectres sont étalés : Au lieu d'avoir un pic on a une espèce de grosse cloche.
On se retrouve alors à devoir trouver un compromis : Une trame suffisamment courte pour pouvoir considérer le signal qu'elle contient comme périodique (quasi-périodique), mais suffisamment longue pour y retrouve les "pics" que l'on s'attend à trouver.

Anonyme

970

56 Posté le 21/09/2014 à 02:14:09

Bien sûr qu'on peut calculer un spectre de n'importe quel signal, pas besoin qu'il soit périodique. Quand on filtre un bruit blanc, on peut atténuer les aigus ou les graves, c'est bien la preuve qu'il comporte des composantes haute et basse fréquence. Maintenant si on cherche une fondamentale et des harmoniques (les pics dont vous parlez) ben on en trouvera pas vu que c'est un bruit et non pas une note, maintenant on peut quand même calculer la transformé de Fourier d'un bruit ou de n'importe quel signal...

Après, effectivement, il y a le fait qu'un signal réel est un signal théorique infini multiplié par une fonction porte (qui vaut 0 en dehors de la mesure, et 1 pendant). Alors comment la durée de la fenêtre influence le spectre, je ne m'en souviens plus... :?!:

mais si le signal mesuré est précis en fréquence, j'imagine qu'on doit avoir des raies bien précises, même si la durée de mesure est très courte non ?

Edit.
Je viens de trouver, page 7 :
http://www.cpge-brizeux.fr/casiers/jnb/cours/tp-tpcours/analyse-de-fourier.pdf
En fait, le spectre du sinus est simplement une raie (enfin plutôt une positive et une négative), et le spectre de la fonction porte est un sinus cardinal dont la largeur du lobe central est inversement proportionnelle à la durée de la porte. Le sinus de durée finie est le produit du sinus infini par la fonction porte, et quand on passe dans le domaine fréquentiel, la multiplication devient une convolution, et donc le spectre du sinus de durée fini est la convolution du sinus cardinal par les deux raies, ce qui donne en fait deux sinus cardinaux centrées non pas sur 0 mais sur les fréquences des deux raies. Donc au lieu d'avoir deux raies, on se retrouve avec deux "lobes" et des "rebonds", ces lobes étant d'autant plus étroits que la durée de la mesure est grande.
Merci pour l'explication, je ne me rappelais plus du tout de cela...

Du coup, pour un signal de type bruit, dans lequel il n'y a aucun fréquence qui prédomine, est-ce qu'on peut aussi dire que c'est la convolution d'un sinus cardinal avec un spectre comportant plein de raies ? Auquel cas, le spectre résultant doit être inexploitable... :???:

Du coup, je me demande, les spectres affichés par les analyseurs de spectre sont-ils fiables ? Et quelles astuces utilisent-ils pour compenser ce problème de fenêtrage ?

[ Dernière édition du message le 21/09/2014 à 05:47:02 ]

*Seed*

11685

Drogué·e à l’AFéine

Membre depuis 18 ans

57 Posté le 21/09/2014 à 08:06:38

autant en forcant un peu j'ai fini par saisir 2/3 notions, autant le post précédent est obscur, du vrai charabia.... :-D

on est plus tellement dans la vulgarisation là. la vulgarisation a pour but de rendre les choses intelligibles au plus grand nombre il me semble mais là je doute que les non initiés y comprennent quoique ce soit. je fais de la musique en amateur depuis 20 ans et j'ai rien compris au post de tchandra....dommage :???:

Sysex and sun

https://soundcloud.com/sensei_syd

Anonyme

261

58 Posté le 21/09/2014 à 09:29:01

Hé, Tchandra c'est un sacré intello !
Personnellement je n'ai même pas essayé de le lire . :D:

(Je déconne, je verrai ça sans doute plus tard après avoir tondu la pelouse )

trazom

1819

AFicionado·a

Membre depuis 20 ans

59 Posté le 21/09/2014 à 09:54:36

Citation :

autant en forcant un peu j'ai fini par saisir 2/3 notions, autant le post précédent est obscur, du vrai charabia....

On a franchement quitté la vulgarisation, là. Fourier, si on veut être précis, c'est très compliqué, surtout quand on arrive dans les questions sur les domaines d'applications, les convolutions, les restrictions, les signaux non périodiques, et les marges d'erreurs en fonction du dernier terme de la série et selon la norme choisie. Pas exigé pour l'agrégation de mathématiques, par exemple.

[ Dernière édition du message le 21/09/2014 à 11:59:05 ]

EraTom

2282

AFicionado·a

Membre depuis 14 ans

60 Posté le 21/09/2014 à 12:11:39

Citation :

Mais les discussions sur les limites de Fourier, on est au delà de l'agrégation de maths, alors, franchement...

On a quitté la vulgarisation mais ce qui est raconté dans la première partie du post de Tchandra est faux ou inexacte (désolé Tchandra, je ne cherche pas à être cassant en ne prenant pas de gant mais c'est pour que ce soit clair).

Sans retenir les brides de démonstration ou le jargon on peut au moins retenir les "conclusions" parce qu'il s'agit simplement de savoir ce que l'on obtient lorsque l'on estime par la mesure (et le calcul) le spectre d'un signal.
Je vais quand même balancer quelques "gros mots" pour que ceux que ça intéressent puissent creuser avec Google.

Citation :

Bien sûr qu'on peut calculer un spectre de n'importe quel signal, pas besoin qu'il soit périodique.

Je n'ai pas dit le contraire. C'est la décomposition en série de Fourier (la somme de sinusoïdes harmoniques) qui n'est applicable que pour les signaux périodiques.

Calculer un spectre ou une "densité spectrale de puissance" ce n'est pas en faire la décomposition en une somme de sinusoïdes.
En gros, calculer un spectre revient à estimer la puissance du signal sur différentes bandes de fréquences, et effectivement ça peut s'appliquer à tout signal. L'outil mathématique utilisé est la transformée de Fourier (+ des outils de probabilité pour traiter correctement les bruits : On estime l'espérance mathématique du carrée du module de la transformée de Fourier).

Lorsque le signal est périodique l'estimation (correcte) de son spectre donne des pics de puissance bien localisés qui correspondent aux puissances de chaque sinusoïde que l'on retrouve avec la décomposition en série.

Si l'on calcule "l'espérance mathématique du carrée du module de la transformée de Fourier" c'est que le signal réel contient toujours du bruit. Si la puissance du bruit est négligeable devant la puissance du signal d'intérêt on peut s'en passer, sinon...
On peut aussi se retrouver dans le cas où c'est justement le bruit qui nous intéresse (comme le souffle d'un instrument à vent, les consonnes d'un signal de parole, ...).

Dans la pratique, on estime l'espérance mathématique en faisant la moyenne empirique de plusieurs trames (ou plusieurs périodes) de temps du même signal et ce n'est possible que si le signal est "ergodique stationnaire au sens large". On dit que l'on peut estimer "la moyenne d'ensemble" à partir de la "moyenne temporelle".
Un transitoire n'est pas stationnaire ; ça ne marche pas.

Concrètement, un coup de cymbale ou de caisse claire qui donne un signal bref, transitoire avec une composante de bruit importante (qui fait bien parti du son lui-même), ne pourra pas être correctement "lu" avec un spectre : Pour une analyse il faut utiliser les méthodes paramétriques (que je ne détaillerai pas) ou, plus simplement pour l'ingé son qui règle ses EQ, faire confiance à ses oreilles.

Citation :

Après, effectivement, il y a le fait qu'un signal réel est un signal théorique infini multiplié par une fonction porte (qui vaut 0 en dehors de la mesure, et 1 pendant). Alors comment la durée de la fenêtre influence le spectre, je ne m'en souviens plus... mais si le signal mesuré est précis en fréquence, j'imagine qu'on doit avoir des raies bien précises, même si la durée de mesure est très courte non ?

Il ne faut pas confondre précision et résolution. La résolution d'un appareil est sa capacité à distinguer une (petite) variation. Ici c'est la capacité à distinguer deux fréquences proches.

La "porte" c'est le fenêtrage temporel, ou tout simplement le fait de prélever une "tranche de signal" pour l'analyser, qui revient à faire le produit de convolution du périodogramme du signal avec la transformée de Fourier de la fenêtre. Pour la porte c'est un sinus cardinal (la fonction sin(x)/x).
Comme tu le dis, là où l'on devrait avoir un pic on se retrouve avec un truc qui la forme du sinus cardinal.

Il existe d'autres fenêtres que la porte (Blackman, Hamming, Bartlett, ...) qui permettent notamment de limiter les lobes secondaires que l'on observe avec une simple porte.
Ça évite des artefacts mais ça ne permet pas d'éviter "l'étalement spectral". Celui-ci est causé par une limite infranchissable démontrée par le théorème d'incertitude Heisenberg-Gabor qui montre que l'on ne peut pas infiniment localiser un signal conjointement dans le domaine temporel et le domaine fréquentiel.

Concrètement, au lieu d'avoir des pics on a des trucs en forme de cloche. Plus le signal est court dans le temps, plus la cloche est étalée (quelque soit le choix de la fenêtre).
Si deux "cloches" sont proches elles se mélangent : Au lieu d'avoir deux cloches pour les deux fréquences on en obtient une grosse qui somme les deux.
Du coup, il est impossible de dire s'il s'agit de 2 sinusoïdes proches ou d'une seule sinusoïde avec une puissance plus importante.
Ça pose un problème supplémentaire pour l'analyse fréquentielle des signaux de courte durée et les transitoires.

Citation :

Du coup, pour un signal de type bruit, dans lequel il n'y a aucun fréquence qui prédomine, est-ce qu'on peut aussi dire que c'est la convolution d'un sinus cardinal avec un spectre comportant plein de raies ? Auquel cas, le spectre résultant doit être inexploitable...

Il ne faut pas raisonner en terme de "raies" mais en terme de bande de fréquence contenant une puissance (ou une énergie).

Quand la bande est "infiniment étroite" c'est une raie (cadeau pour les plaisanteries grivoises).

Pour un bruit on s'intéresse à l'enveloppe de la densité de puissance, à son niveau sur une largeur de bandes à préciser. Ça na pas vraiment de sens de regarder ce qu'il se passe à une fréquence données. Finalement, le problème de l'étalement est un peu moins critique.

Hors sujet :

D'ailleurs, lorsqu'un constructeur sérieux donne un SNR c'est généralement le rapport entre la puissance d'une sinusoïde @1kHz (pour l'audio) et la puissance du bruit sur une bande de 20Hz-20kHz.
Si le constructeur annonce pouvoir restituer une bande plus large... Il faudrait qu'il intègre le bruit sur toute cette bande pour annoncer son SNR.

Parfois (souvent) il y a des arnaques : Le SNR est donné comme le rapport entre le pic @1kHz et le niveau du bruit sur cette même fréquence dans un calcul du spectre. Ce calcul est avantageux pour le constructeur mais faux : La puissance du bruit ne peut pas être réduite à une bande étroite autour de 1kHz... C'est comme ça que certains arrivent à gratter 20 à 40dB sur leur SNR.
Si un SNR est donné sans préciser la bande de fréquence alors il y a sans doute une arnaque.

Citation :

Du coup, je me demande, les spectres affichés par les analyseurs de spectre sont-ils fiables ? Et quelles astuces utilisent-ils pour compenser ce problème de fenêtrage ?

Fiables jusqu'à certaines limites. On peut rapidement faire n'importe quoi en cherchant à analyser des signaux qui ne peuvent pas l'être correctement à un périodogramme.

Je crois que l'on a fait le tour des pièges :
- Tu ne peux être sûr d'obtenir un truc pertinent que sur les sons qui ne varient pas trop vite dans le temps,
- Dès qu'il y a beaucoup de transitoires réduis la durée des trames... En te rappelant que tu étales le spectre,
- Pour les bruits, souffles, etc. ne cherche pas des raies mais pense en terme de bandes et d'enveloppe spectrales,
- Pour le fenêtrage, il est important de choisir une fenêtre qui évite que les lobes secondaires soient trop prononcés (Hamming par défaut c'est très bien). Pour l'étalement il n'y a, finalement, que la durée des trames d'analyses qui permet de le régler.
- Et, surtout, si les conditions ne sont pas réunies mets de côté les analyseurs de spectre et fais plus confiance à tes oreilles !

[ Dernière édition du message le 21/09/2014 à 12:13:08 ]

miles1981

8370

Je poste, donc je suis

Membre depuis 21 ans

61 Posté le 21/09/2014 à 13:53:19

Je maintiens. Tout signal peut être décrit sous la forme de somme de sinusoïdes. Je n'ai pas parlé de série de Fourier. Le cas général de la transformée de Fourier est bien à l'origine pour tout signal, périodique ou non.
Lorsque le signal est périodique, les sinusoïdes ont une caractéristique qui est qu'elles ont une fondamentale commune (série de Fourier).
Encore une fois, on essaie de vulgariser, et on n'utilise pas les bons termes et on ne lit pas tout.

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

Danguit

3348

Squatteur·euse d’AF

Membre depuis 19 ans

62 Posté le 21/09/2014 à 14:02:05

Citation :

Si deux "cloches" sont proches elles se mélangent : Au lieu d'avoir deux cloches pour les deux fréquences on en obtient une grosse qui somme les deux.

Pas toujours grosse puisque c'est dans ce cas que l'on peut voir (et/ou entendre) le battement.

Passer pour un idiot aux yeux d'un imbécile est une volupté de fin gourmet. (G. Courteline)

KaeRZed

12036

Drogué·e à l’AFéine

Membre depuis 21 ans

63 Posté le 21/09/2014 à 14:15:39

J'ai beau essayer de tout lire et relire... Y'a pas moyen...

Mes Compos Inspirées pour AF - Soundcloud

Danguit

3348

Squatteur·euse d’AF

Membre depuis 19 ans

64 Posté le 21/09/2014 à 14:38:48

Une petite manip toute fraîche et un petit graphe pour montrer l'impact de la bande de résolution : somme de deux sinusoïdes à #10kHz séparées de 50Hz.
En haut une bande de #1.2Hz (sans tenir compte du facteur de correction de la fenêtre) => 2 raies stables,
en bas une bande de #120Hz => 1 raie plus large dont le niveau fluctue au rythme du battement (2 relevés à la volée).
image.php

Passer pour un idiot aux yeux d'un imbécile est une volupté de fin gourmet. (G. Courteline)

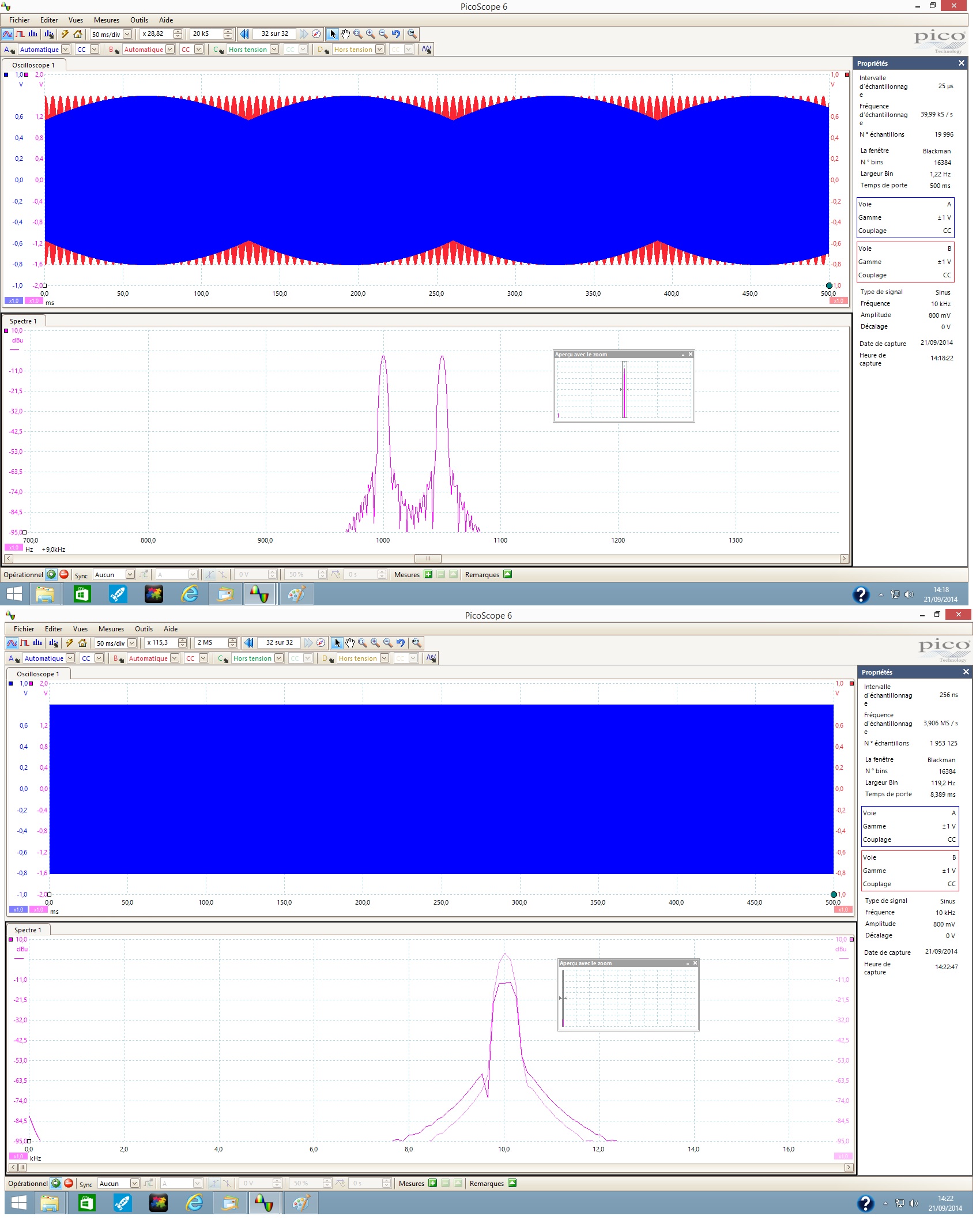
EraTom

2282

AFicionado·a

Membre depuis 14 ans

65 Posté le 21/09/2014 à 15:59:39

Citation :

Pas toujours grosse puisque c'est dans ce cas que l'on peut voir (et/ou entendre) le battement.

Citation :

Je maintiens. Tout signal peut être décrit sous la forme de somme de sinusoïdes.

Oui ok, envoie les fondements de l'analyse non standard et tu auras (presque) raison.

La question n'est pas tant de savoir "si l'on peut" mais plutôt de savoir si l'on obtient quelque chose d'exploitable. Or tu n'obtiendras pas un outil efficace pour analyser / manipuler / représenter / synthétiser un signal qui s'écarte trop du signal périodique :fleche:

Cf. ondelettes et modèle ARMA.

Je pourrais étayer en renvoyant vers toute une littérature qui commence avec les travaux pour le traitement de la parole (que j'imagine tu dois connaître) mais je pense que c'est typiquement le genre de "débats d'experts" qui n'aide personne ici.

[ Dernière édition du message le 21/09/2014 à 16:43:59 ]

*Seed*

11685

Drogué·e à l’AFéine

Membre depuis 18 ans

66 Posté le 21/09/2014 à 16:08:14

ben moi, à part le coup de la bande infiniment étroite qui est une raie j'ai rien tâté à ton post, je sais même pas de quoi tu parles ni dans quel but tu le fais :bravo:

Sysex and sun

https://soundcloud.com/sensei_syd

EraTom

2282

AFicionado·a

Membre depuis 14 ans

67 Posté le 21/09/2014 à 16:37:54

Je répondais surtout à Tchandra qui se posait des questions sur l'analyse spectrale.

[ Dernière édition du message le 21/09/2014 à 16:38:32 ]

Anonyme

970

68 Posté le 21/09/2014 à 19:58:26

Citation de Senseï Syd :

autant en forcant un peu j'ai fini par saisir 2/3 notions, autant le post précédent est obscur, du vrai charabia....

Euh oui, pardon... je posais des questions à EraTom, du coup on est plus du tout dans la vulgarisation en effet :oops:

Il faut une culture mathématique pour saisir le vocabulaire, sinon, c'est incompréhensible en effet. Même si c'est pas si compliqué que ça en a l'air, tant qu'on entre pas dans les calculs, intégrales et compagnie :nawak:

Citation de EraTom :

Calculer un spectre ou une "densité spectrale de puissance" ce n'est pas en faire la décomposition en une somme de sinusoïdes.
En gros, calculer un spectre revient à estimer la puissance du signal sur différentes bandes de fréquences, et effectivement ça peut s'appliquer à tout signal. L'outil mathématique utilisé est la transformée de Fourier

Merci pour ta réponse

Par contre, c'est curieux cette histoire de puissance dont tu parles. Ce que j'avais retenu, c'est que transformée de Fourier est une projection d'une fonction sur une base de type exp(2Pi.f.t) avec f réel (alors qu'il s'agit de nombres entiers pour la décomposition en série) et que ça s'appliquait à tout signal... donc pour moi le spectre, ça indique simplement l'amplitude de telle ou telle composante (haute fréquence, basse fréquence etc) pas la puissance... :?!:

en général quand on calcule une puissance ou une énergie, on utilise le carré du signal à un moment donné, mais bon si tu dis que le spectre donne une idée de la puissance du signal en fonction de la bande de fréquence, je te crois mais je ne pige pas d'où ça vient...

Citation :

Dans la pratique, on estime l'espérance mathématique en faisant la moyenne empirique de plusieurs trames (ou plusieurs périodes) de temps du même signal et ce n'est possible que si le signal est "ergodique stationnaire au sens large".

J'ai pas tout compris...
Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...

Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal... :noidea:

Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...

Citation :

Il existe d'autres fenêtres que la porte (Blackman, Hamming, Bartlett, ...) qui permettent notamment de limiter les lobes secondaires que l'on observe avec une simple porte.
Ça évite des artefacts mais ça ne permet pas d'éviter "l'étalement spectral". Celui-ci est causé par une limite infranchissable démontrée par le théorème d'incertitude Heisenberg-Gabor qui montre que l'on ne peut pas infiniment localiser un signal conjointement dans le domaine temporel et le domaine fréquentiel.

Ah oui, c'est vrai qu'on peut utiliser d'autres enveloppes que la "porte", des gaussiennes ou je sais plus quoi :bravo:

J'avais oublié ce truc... Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...

Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?

[ Dernière édition du message le 21/09/2014 à 20:01:04 ]

Choc

6968

Membre d’honneur

Membre depuis 22 ans

69 Posté le 21/09/2014 à 20:51:45

Lol

Certaines personnes doivent halluciner en lisant les post de ce forum...Enfin, bon, la moitié des protagonistes doit être BAC+5 voir docteur en traitement du signal.

D'ailleurs, pourquoi une telle concentration de signaleur sur ce forum ? Est ce que c'est la musique qui a emmené ces personnes à faire du signal où alors est-ce le chemin inverse ?

Pour les problèmes de l'analyse spectrale, c'est très complexe. Par contre, je relativiserai un peu certains discours. En effet, même si les soucis de resolution spectrale sont importants dans certaines applications (genre militaire), ce n'est pas forcement le cas pour l'analyse des signaux audios. Franchement, la transformée de Fourier Discrète ca marche déjà super bien...(et on peut démontrer que cette technique est équivalente au MV lorsque N tend vers l'infini, le MV possédant la super propriété d'atteindre asymptotiquement la borne de Cramer Rao)

Pour illustrer tout ces phénomènes, je vous conseille de jeter un coup d'oeil sur mon appli: www.sp4mass.com

Vous allez dans l'application "Signal App"
Vous allez dans Synthetic Signal puis vous generez un signal de votre choix (sinusoïde dans du bruit, deux sinusoïdes etc). Vous appuyez sur Save
Dans le menu, vous appuyez sur le bouton Freq et vous aurez à votre disposition le nec plus ultra des techniques d'analyse spectrale: Fourier (Periodogramme), Periodogramme de Welch, MUSIC et ESPRIT

Site personnel: https://www.enib.fr/~choqueuse/

trazom

1819

AFicionado·a

Membre depuis 20 ans

70 Posté le 21/09/2014 à 21:07:06

Citation :

Enfin, bon, la moitié des protagonistes doit être BAC+5 voir docteur en traitement du signal.

Et les autres sont partis.

KaeRZed

12036

Drogué·e à l’AFéine

Membre depuis 21 ans

71 Posté le 21/09/2014 à 21:45:39

Ou sur le point de se barrer en courant... pour faire de la musique !

Mes Compos Inspirées pour AF - Soundcloud

Anonyme

970

72 Posté le 21/09/2014 à 22:22:36

Ah pardon d'avoir posé des questions d'analyse spectral sur un forum d'audio...

, ça n'empêche pas les gens de lire l'article ou de zapper les discussions qui ne les intéressent pas...

Citation :

Franchement, la transformée de Fourier Discrète ca marche déjà super bien...

Ben c'est ce qu'il me semble aussi, mais EraTom dit que ce n'est pas exploitable sur les transitoires...

[ Dernière édition du message le 22/09/2014 à 00:13:25 ]

KaeRZed

12036

Drogué·e à l’AFéine

Membre depuis 21 ans

73 Posté le 22/09/2014 à 07:24:21

Tchandra, tu as le droit de poser toutes les questions que tu souhaites.... Dès l'instant qu'elles sont posées dans une discussion en rapport.
Tes questions très techniques ont tout-à-fait leur place sur AF, mais peut-être moins dans une discussion traitant d'initiation... Ce qui n'enlève rien à leur intérêt !
Maintenant, faut pas se vexer, hein... Ce n'est que mon humble opinion qui ne vaut que ce qu'elle vaut...
:-D

Hors sujet :

De même que tu auras le droit de poser des questions très pointues sur la méthode de tapping utilisée par Yngwie Malmsteen mais, dans une discussion nommée "Initiation à la Guitare: comment jouer les Jeux Interdits", ça va faire un peu HS...

Mes Compos Inspirées pour AF - Soundcloud

[ Dernière édition du message le 22/09/2014 à 07:32:04 ]