Anatomie des ondes sonores - La synthèse sonore - 2e partie

Une onde sinu­soï­dale seule comme celle repré­sen­tée à la fin du précé­dent article est une onde « simple ». On ne rencontre pas de son abso­lu­ment « pur » dans la nature. Ce qui pour­rait s’en rappro­cher le plus, c’est le son d’un diapa­son ou celui émis, dans certaines condi­tions, par un instru­ment de… synthèse sonore ! Vous commen­cez à comprendre pourquoi je vous parle de tout cela, non ?

Dès qu’à une onde simple on ajoute ne serait-ce qu’une seule autre onde non iden­tique à la première, on obtient une nouvelle onde, dite « complexe ». Eh oui, si on pousse le raison­ne­ment, cela signi­fie que, quel que soit le nombre de sources sonores qui sont enre­gis­trées à un instant « t » – imagi­nons par exemple tout un orchestre sympho­nique qui joue, sans oublier les réver­bé­ra­tions acous­tiques de la salle, la dame qui éter­nue à gauche et le monsieur qui ronfle à droite – la repré­sen­ta­tion de l’en­re­gis­tre­ment ne montre qu’une seule et même onde complexe, compo­sée à fois d’ondes dites pério­diques (les notes de musique, comme nous le verrons plus bas) et de sons dits « non pério­diques » (l’éter­nue­ment et le ronfle­ment, par exemple).

Pour infor­ma­tion, on doit au génial mathé­ma­ti­cien et physi­cien Joseph Fourier (1768–1830) la décou­verte suivante : toute onde complexe peut être décom­po­sée en un certain nombre d’ondes sinu­soï­dales simples, à l’ex­cep­tion des tran­si­toires, qui sont les périodes d’éta­blis­se­ment et de dispa­ri­tion du son.

Bien, nous avons évoqué jusque-là l’am­pli­tude et la période des ondes… mais de quoi s’agit-il exac­te­ment ?

La longueur compte !

Les prin­ci­pales carac­té­ris­tiques d’une onde sonore simple sont son ampli­tude, sa période, sa longueur d’onde, sa phase et sa fréquence, à laquelle nous consa­cre­rons l’in­té­gra­lité du prochain article.

L’onde qui se propage dans un milieu donné entraine des varia­tions de pres­sion dans ledit milieu (plus exac­te­ment une alter­nance pres­sion/dépres­sion). Ce sont ces varia­tions qui sont repré­sen­tées par l’am­pli­tude. Elles sont expri­mées en Pascal.

Imagi­nons une corde de guitare. Au repos, elle sera en « posi­tion d’équi­libre ». Si nous la faisons vibrer, elle se dépla­cera plus ou moins loin au-dessus, puis en dessous de sa posi­tion d’équi­libre, avant d’y reve­nir. L’am­pli­tude du mouve­ment de la corde repré­sente la diffé­rence entre son dépla­ce­ment maxi­mal dans un sens donné et son point d’équi­libre.

L’am­pli­tude d’une onde repré­sente la diffé­rence entre son point d’équi­libre et le niveau maxi­mal de pres­sion ou de dépres­sion exercé sur le milieu ambiant.

Graphique­ment, on repré­sente le point d’équi­libre par un axe hori­zon­tal. Ce dernier repré­sen­tant le niveau zéro de vibra­tion, donc l’as­pect qu’au­rait l’onde si elle ne vibrait pas, donc si aucun son n’était produit. En consé­quence, plus l’onde vibre autour de cet axe central – donc plus le dessin de l’onde s’éloigne de celui d’une ligne droite hori­zon­tale – plus le volume de son produit est élevé. On peut donc lier direc­te­ment l’am­pli­tude d’une onde sonore au volume du son concerné, exprimé en déci­bels. Dans notre exemple, plus la corde de guitare vibre, et plus le son produit est fort !

À noter que la puis­sance d’une onde – donc son ampli­tude – décroît avec le temps quand elle se propage dans un espace libre, car l’éner­gie de l’onde se répar­tit dans cet espace. Les instru­ments acous­tiques possèdent tous une caisse de réso­nance ou bien un tuyau qui permet de dimi­nuer la disper­sion de l’onde sonore dans l’es­pace, et donc de dimi­nuer la perte de puis­sance. En synthèse sonore, nul besoin d’une caisse de réso­nance puisque l’on peut agir direc­te­ment sur l’onde et entre­te­nir indé­fi­ni­ment la produc­tion de son, comme nous le verrons.

Dès qu’une forme d’onde simple est répé­tée dans le temps, on dit qu’elle est « pério­dique », car elle est compo­sée de cycles qui se répètent. On désigne d’ailleurs par  « période » le temps que la forme d’onde met pour effec­tuer un cycle complet. La longueur d’onde quant à elle repré­sente la distance entre 2 cycles de la forme d’ondes.

En phase

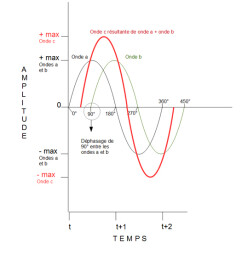
Enfin, avant d’abor­der les fréquences dans le prochain article, un mot sur la phase. Sans entrer dans des détails trigo­no­mé­triques un peu hors sujet ici, sachez que la phase se mesure en degrés, et qu’en ce qui nous concerne, nous musi­ciens, elle se défi­nit surtout en fonc­tion… de l’écart de phase ou non avec une autre onde !

Si on mélange deux ondes, a et b, abso­lu­ment iden­tiques, mais qu’on fait démar­rer l’onde b au degré 90 de l’onde a, on dira que ces deux ondes sont dépha­sées entre elles de 90°.

Qu’est-ce que cela implique au niveau sonore que des ondes soient en phase ou non ?

La phase peut avoir des réper­cus­sions diffé­rentes sur le compor­te­ment du son. Les ampli­tudes de deux ondes s’ad­di­tionnent. Comme nous l’avons vu, c’est de l’am­pli­tude de l’onde que dépend direc­te­ment le volume du son. Si nous mélan­geons deux sons « en phase », les parties posi­tives des deux ondes vont s’ad­di­tion­ner entre elles, et les parties néga­tives vont faire de même. Le tout aura donc pour résul­tat un double­ment du volume géné­ral du son.

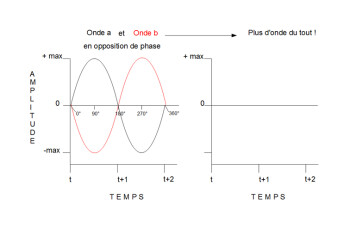
Au contraire, si l’on mélange deux sons « en oppo­si­tion de phase » complète, les parties néga­tives d’une onde vont annu­ler les parties posi­tives de l’autre, et vice-versa, entraî­nant une mise à zéro des ampli­tudes, donc des volumes des deux sons, donc des deux formes d’onde elles-mêmes, donc… le silence absolu !

Entre la parfaite concor­dance de phases et la parfaite oppo­si­tion se situe natu­rel­le­ment toute la gamme des possi­bi­li­tés. À noter que certains effets que vous avez peut-être déjà expé­ri­men­tés tels qu’un « phaser » ou un « flan­ger » reposent sur le juste dosage entre concor­dance et oppo­si­tion de phase entre les ondes.