Ces quelques chapitres aborderont de manière très progressive les notions de base du son dans le but de mieux comprendre certains points clés de la lutherie électronique.
Pour commencer, quelques évidences, cependant indispensables à la suite de ces articles. L’ouïe est le sens qui nous permet de percevoir les sons : notre cerveau reçoit des stimuli captés par nos tympans, eux-mêmes mis en oscillation par les variations de pression d’air de notre environnement. Ces variations sont produites naturellement par la nature (choc entre deux objets, vibration des cordes vocales de nos congénères, etc.) ou provoquées par les déplacements alternatifs de la membrane d’un haut-parleur.
La fondamentale et la représentation de la forme d’onde
Ces oscillations plus ou moins régulières peuvent être représentées de plusieurs façons. Prenons comme exemple simple l’onde sinusoïdale :
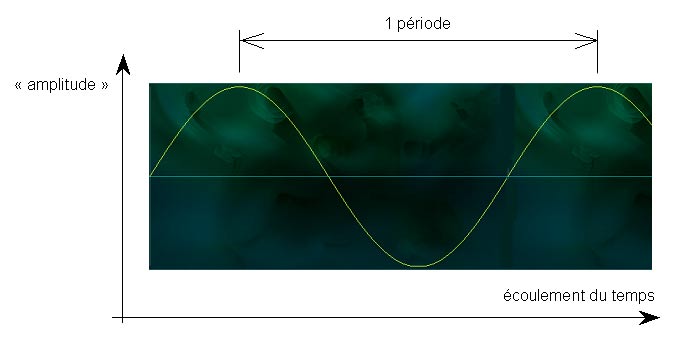
Horizontalement, on représente l’écoulement du temps et verticalement ce qu’on appelle l’amplitude. Cette amplitude représente la variation de la pression acoustique (celle de l’air et celle sur notre tympan) ou aussi la distance du déplacement avant-arrière de la membrane du haut-parleur, qui pousse l’air lorsque la membrane se déplace vers l’avant et l’aspire lorsqu’elle se déplace vers l’arrière.
La période représente la durée qui sépare 2 instants de pression maximale. S’agissant d’une durée, elle est exprimée en secondes. On exprime plus souvent cette oscillation par le nombre de périodes qui apparaissent pendant 1 seconde, c’est la fréquence, exprimée en Hz (fréquence = 1/période).
Pour une note de ‘La’ au milieu d’un clavier de piano, cette fréquence est communément de 440 Hz, à savoir que l’oscillation se répète 440 fois chaque seconde. Cela revient à imaginer sur l’illustration que la durée d’une période est de 0,002272 seconde ! Plus la fréquence est basse, plus le son est grave, et inversement.
Voilà ce qu’on entend. Ce n’est certes pas très musical, mais la lutherie électronique va justement nous permettre d’en tirer pleinement profit : nous en reparlerons.
Représentation du spectre sonore
Les ondes peuvent être représentées d’une autre façon, à savoir par leur contenu plus ou moins riche en différentes composantes, c’est leur spectre sonore.
Pour cette représentation, l’axe horizontal n’est cette fois pas l’écoulement du temps, mais le support d’une graduation où l’on trouve les sons les plus graves à gauche et les sons les plus aigus à droite. L’axe vertical représente la quantité de chacune de ces composantes qui font partie du son complet. Voici le profil spectral de l’onde sinusoïdale :
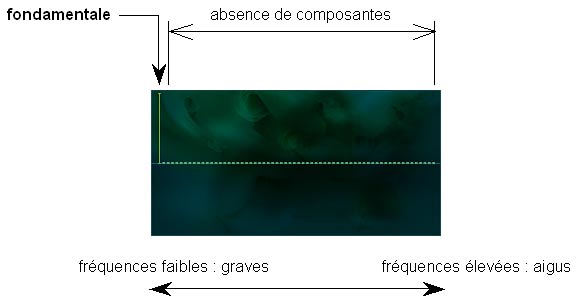
On constate que l’onde sinusoïdale ne contient qu’une seule composante, la barre verticale jaune, tout à gauche du spectre et qui est la fondamentale. Du fait de cette seule composante, l’onde sinusoïdale est l’onde la plus élémentaire qui soit.
Il est important de se familiariser avec ces 2 représentations (onde et spectre) puisque nous ajouterons des harmoniques à ce son de base : nous en verrons très clairement la forme d’onde et le spectre, et entendrons parfaitement ce qu’elles représentent pour un son complexe !
Les harmoniques et les composantes du spectre sonore
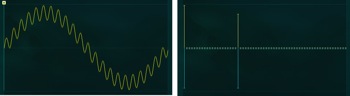
Après avoir expérimenté la relation entre les représentations graphiques d’un son (onde et spectre) et le résultat ‘à l’oreille’, nous pouvons superposer à notre onde sinusoïdale (la fondamentale) une seconde onde sinusoïdale, ayant une fréquence plus élevée et qui produit donc un son plus aigu.
À gauche, la forme d’onde, à droite, le spectre :
Note : concernant le spectre, on a vu dans la partie (1) que les barres jaunes qui se déploient vers le haut représentent l’amplitude de chaque harmonique. Les barres bleues vers le bas représentent leurs phases. Elles n’ont pas d’action audible pour les sons que nous utilisons ici, aussi est-il inutile de s’en préoccuper. On en reparlera cependant dans un prochain chapitre.
Sur cette figure, on constate une première oscillation d’ensemble dont la période couvre toute la plage visible, ce qui correspond à la fondamentale. Cette fondamentale supporte une seconde oscillation, plus fine. Dans cet exemple, il s’agit de l’harmonique de rang 22 qui comprend 22 oscillations durant la seule oscillation de la fondamentale. Elle est donc à une fréquence 22 fois supérieure aux 440 Hz de la fondamentale, à savoir 9680 Hz.
Voici le résultat sonore : on entend distinctement ces 2 oscillations de façon individuelle : la fondamentale seule pour commencer, puis l’harmonique qui s’y rajoute. On dirait vraiment 2 sons différents.
Vers un son complexe
Si l’on ajoute encore et encore des harmoniques, on finira par ne plus percevoir individuellement toutes les composantes du son global : il s’agira d’une onde complexe telle que produite par un instrument acoustique ou tout autre phénomène naturel.
La vidéo suivante en présente une illustration complète.
Harmoniques inharmonieuses
Les sons présentés ici ont tous été composés de fréquences dites ‘harmoniques’ car multiples entiers de la fondamentale. Par exemple 2 × 440 pour le rang 2 du La, 3 × 440 pour son rang 3, etc. Si une ou plusieurs composantes sont à des fréquences différentes de multiples entiers, le son sera inharmonique. Par exemple 2,565 × 440 Hz, etc. : c’est le cas des instruments de type cloche et bon nombre de percussions. Puisque ces harmoniques ne sont plus harmonieuses, on préfère les désigner autrement, ce sont les partiels.
Le timbre
Pour l’instant, seul le son (ou onde sonore) a été évoqué, or pour un instrument de musique, ou une voix, on parle de timbre.
-
le son est le résultat du spectre sonore audible durant une période de la fondamentale, ou durant une succession de périodes si elles se suivent cycliquement de façon identique,
-
le timbre prend en compte l’évolution du son dans le temps : le son de l’attaque d’une note peut être très différent du son maintenu et de son extinction progressive. On parle de timbre pour l’ensemble de la note perçue lorsque le spectre est évolutif.
L’idée de la synthèse
Puisqu’il est possible de réduire toute sonorité en un profil spectral, on peut imaginer qu’un dispositif électronique capable de produire ces oscillations soit aussi capable d’imiter tout instrument acoustique. On peut même rêver à explorer un tout nouveau champ de sonorités inédites…
On verra comment exploiter pour un usage musical ces sonorités somme toute très élémentaires, et pas très agréables (!).
Fréquences et progression des harmoniques
Nous avons vu que les harmoniques se succédaient à partir de la fondamentale selon un principe très simple : pour passer d’une harmonique à la suivante, on lui ajoute la fréquence de la fondamentale. Cette idée se transcrit facilement comme ceci :
Fréquence de l’harmonique de rang (n) est égale à la Fréquence de l’harmonique de rang (n-1) + la Fréquence de la fondamentale
ou encore :
F h(n) = F h(n-1) + F f
Partant du La à 440 Hz, qui est la référence communément admise aujourd’hui, on obtient les valeurs de la colonne de gauche du tableau 1 ci-dessous :
f : 440
rang 2 : 440 + 440 = 880
rang 3 : 880 + 440 = 1320
rang 4 : 1320 + 440 = 1760
rang 5 : 1760 + 440 = 2200
etc.
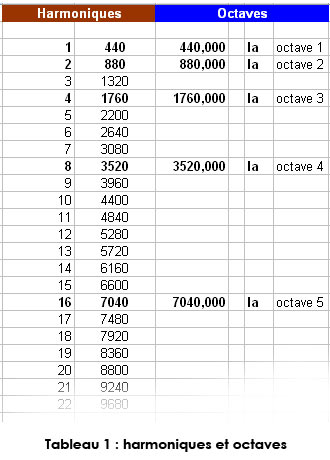
Note : le résultat est le même si on multiplie la fréquence de la fondamentale par le numéro de rang de l’harmonique, mais la méthode de l’addition permet de mieux différencier cette notion de celle de la progression des octaves.
Progression des octaves
La définition de l’octave est la suivante : chaque octave est à une fréquence double de la précédente. On peut aussi dire qu’elles se succèdent par multiplication (et non par addition comme les harmoniques !) avec un facteur de 2.
F octave(n) = F octave(n-1) x 2
Si l’on part à nouveau du La à 440 Hz (tableau 1 ci-dessus) :
f : 440
octave 2 : 440 × 2 = 880
octave 3 : 880 × 2 = 1760
octave 4 : 1760 × 2 = 3520
etc.
On constate que les La des octaves successives correspondent exactement aux harmoniques de rang 1, 2, 4, 8, 16, 32, 64, etc., ce qui est réjouissant, car cela semble bien simple.
Comparaison de la progression des harmoniques et des octaves
Puisque nous avons d’une part une série d’harmoniques croissantes et d’autre part une série de La à des octaves également croissantes, il est intéressant de les placer sur une même échelle de fréquences :

1. Le repère à gauche est gradué de façon régulière de 500 Hz en 500 Hz.
2. Les harmoniques sont placés sur cette échelle avec un pas, également régulier, de 440 Hz.
3. Les La de chaque octave sont également placés sur cette échelle : on constate immédiatement que les pas d’une octave à l’autre ne sont pas réguliers, ils vont en augmentant.
Octave est sympa, mais il est un peu grossier
Imaginez-vous faire de la musique avec à votre disposition une seule note par octave ?
Il convient de découper chaque octave en un certain nombre de notes pour développer des harmonies et des mélodies moins grossières. L’une des grandes idées, celle qui s’applique à la musique occidentale depuis plusieurs siècles, consiste à découper l’octave en 12 intervalles. On obtient les notes dont nous avons l’habitude : La, La #, Si, etc., autrement dit, la gamme.
La façon la plus évidente de définir la taille des intervalles est de considérer qu’ils soient répartis de façon égale sur l’étendue de chaque octave. On parle de tempérament égal pour cette raison.
En observant une telle progression des notes sur le tableau 2 (pour une question d’encombrement, seules les notes de l’octave 4 ont été désignées), on comprend pourquoi l’on ne peut pas avoir, pour toutes les notes, de coïncidence exacte avec une harmonique d’un rang de valeur entière : les harmoniques évoluent de façon régulière alors que les notes évoluent de façon progressive.
Les fréquences des notes en tempérament égal
On a vu que la progression des octaves se fait par multiplication d’un facteur 2. Si l’on souhaite des notes réparties selon 12 intervalles égaux au sein d’une octave, chaque note doit donc être multipliée par un facteur 2 puisssance 1/12 pour déterminer la note suivante. Cela se traduit par :
F (n) = F (n-1) x 2 exp 1/12
ou aussi
F (n) = F (n-1) x racine 12° de 2
ou F (n) = F (n-1) x 1,059463…
Ainsi
La = 440
La # = 440 × 1,059463 = 466,164
Si = 466,164 × 1,059463 = 493,883
etc.
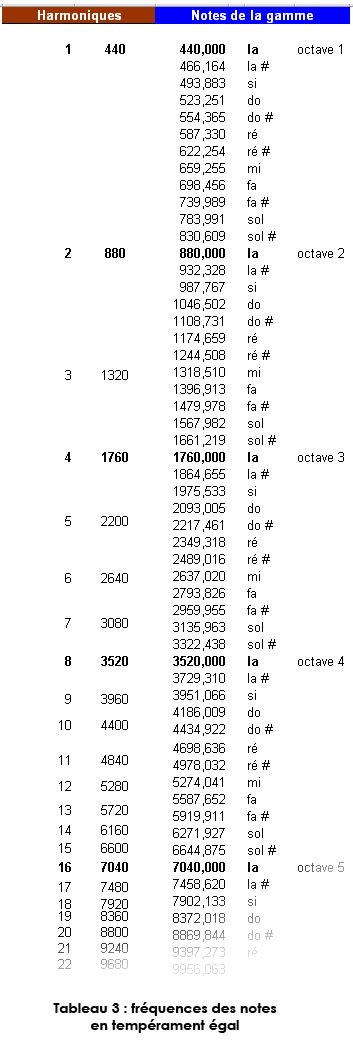
Contrairement au tableau 2 où l’échelle est correcte, j’ai représenté ici la liste des fréquences des notes de façon régulière et j’ai tenté de placer les fréquences des harmoniques à peu près en correspondance.
On vérifie que les fréquences des notes ne coïncident pas toujours avec celles des harmoniques.
Si l’on regarde de plus près les lignes relatives aux harmoniques, on observe que les rangs 1 et 2 coïncident parfaitement avec les la des 2 premières octaves. Le rang 3 correspond à peu de chose près au mi de la 2e octave. Au rang 4, on se retrouve exactement sur un La. Puis au rang 5 correspond à peu près un Do #. Plus loin, les écarts peuvent devenir assez importants.
Il est intéressant de remarquer que les premières notes rencontrées sont La, Mi et Do# ! C’est un accord majeur : le plus harmonieux et le plus simple de tous. Ceci explique probablement cela. Si la série avait été calculée à partir du Do (habituellement 264 Hz) et non à partir du La, ces trois premières notes auraient été Do, Sol et Mi : également un accord majeur bien entendu.
Les autres façons de calculer les gammes
Depuis Pythagore jusqu’aux compositeurs contemporains, par monts et par vaux tout autour de la Terre, on a imaginé de bien belles théories pour répartir les notes au sein des octaves. Ces 12 intervalles peuvent être distribués de bien des façons et on rencontre des systèmes avec davantage d’intervalles, notamment dans les musiques orientales.
Les synthétiseurs actuels permettent pour la plupart l’accord sur des systèmes existants (Pythagore, Werkmeister, Valotti, etc.) et même de créer librement nos propres systèmes. Voici un exemple :
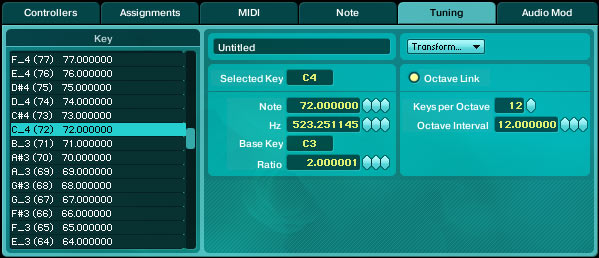
C’est ici la note C_4 qui est en cours d’édition (le Do de l’octave 1 du tableau 3) et sa fréquence est bien de 523,251 Hz. Il suffit de la changer pour réaccorder cet instrument électronique virtuel comme on le ferait d’un piano.
Notez le bouton ‘Octave link’ qui permet, si on l’active, de reproduire automatiquement les réglages d’une seule octave vers toutes les autres.
Pour conclure
Un dernier coup d’oeil sur les tableaux ci-dessus : les octaves tombent toujours juste avec les harmoniques ! Voilà pourquoi l’octave est une base de réflexion intéressante pour élaborer un système de gamme. Mais rien n’y oblige, et la désactivation du bouton ‘Octave link’ de la figure précédente promet des réglages tout à fait innovants.
Précisons encore que ce chapitre a traité des harmoniques contenues dans un son et qu’il a cherché à trouver des équivalences avec les notes de la gamme à tempérament égal. Nous partions de la seule note de La à 440 Hz. Ces tableaux sont simplement à transposer si l’on souhaite connaître les fréquences des harmoniques pour les autres notes de la gamme.
Ainsi, lorsqu’on joue un accord, à savoir plusieurs notes simultanément, chacune des notes va engendrer son propre cortège d’harmoniques au grand complet.
Après ce petit interlude quelque peu théorique, nous reviendrons à la pratique dans la seconde partie de ce dossier pour fabriquer un joli son rien qu’avec ces vilaines et stridentes ondes sinusoïdales… et un peu d’astuce.