Economie-fanzine
- 630 réponses
- 50 participants
- 18 964 vues
- 45 followers
Traumax
Pour parler de la science des idéologies qu'est l'économie.
Tu sais tout des Futures, des cycles schumeteriens, tu es fan de l'école de Chicago mais tu détestes la house ?
Hayek et fais bander mais t'aimes pas les actrices latinos ?
Tu shortes en intraday dans une stratégie win-win sur le forex ?
T'as rien compris aux phrases précedentes, mais tu veux apprendre ?
C'est ici. Les débats idéologiques seront tolérés, dans la limite de la courtoisie argumentée, et de la pédagogie de bon aloi.
Dr Pouet
Ce que je comprends pas du tout chez les investisseurs et la finance, c'est qu'il n'y a pas de recherche fondamentale d'assurer vraiment ses arrières et de lutter radicalement contre le changement climatique. Du vernis vert ça on en voit à tort et à travers, mais les crises à venir vont faire sauter ce vernis comme la pandémie a mis à poil nos dirigeants paumés.
Il semble que beaucoup de chaires d’économie, et donc de directeurs de recherches, soient financés par... la finance. De ce fait, les études effectuées vont beaucoup dans le sens de conforter les décisions déjà prises, aller dans le sens du vent, business as usual etc.. Des statistiques sur les titres des publications dans les revues à comité de lecture semblent bien confirmer ce biais.
[ Dernière édition du message le 23/04/2020 à 17:21:31 ]
KoalaMan
Quelqu'un serait-il compétent pour m'expliquer le fonctionnement de l'inflation intense qui nous pend au nez ?
Je veux dire, en sortie de crise sanitaire, on va sans doute avoir une crise financière, accompagnée d'une belle inflation, histoire d'achever les faibles qui n'ont pas encore tout perdu.
Je comprends le fonctionnement de l'inflation dans un état ou dans une zone avec la même monnaie. Mais là, dans une crise planétaire (ça fait bizarre de l'écrire), la création de monnaie ne va pas se faire de façon identique dans tous les pays.
En gros, comment ça risque de se passer en France ? Et en Suède ?
Je vais passer pour un obscur salopard, mais est-ce qu'il y a des chances que la Suède s'en sorte mieux ? Pas d'arrêt de l'économie, et hors zone euro.
On ne voit bien qu'avec les yeux. Le cœur est invisible pour l'essentiel.
tihouss
L'appétit vient en mangeant ; la réforme, c'est pas sorcier ; le campement léger en plein air, non. Cupidon
Dr Pouet
Sur l’inflation :
Explications des raisons pour lesquelles il n’y a pas de lien direct entre création de monnaie et inflation :
Projacks
Ceux qui déplacent des montagnes... font chier les cartographes.
Dr Pouet
Tout simplement parce-que l'on se fixe souvent comme objectif une variation en pourcentage par rapport à l'année précédente. Si on considère une grandeur A (comme par exemple : PIB, nombre de voitures produites, population...), et que l'on vise une augmentation de 4% entre l'année 0 et l'année 1, on va avoir :
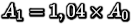
Si on vise également 4% de croissance entre l'année 1 et l'année 2, on aura
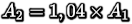 , et ainsi de suite.
, et ainsi de suite.On aura donc :

si ça ne s'affichait pas correctement :
A2 = 1,04 x A1
A2 = 1,04 x 1,04 x A0
A2 = (1,04)² x A0
An = (1,04)^n x A0
L'élévation à la puissance n de cette constante différente de un (1,04) est une exponentielle.
C'est même précisément la définition de l'exponentielle : https://fr.wikipedia.org/wiki/Fonction_exponentielle
J'ai ajouté les mots entre parenthèses par rapport à la définition de la Wikipédia pour la ramener à mon exemple ci-dessus :
Elle est utilisée pour modéliser des phénomènes dans lesquels une différence constante (+1) sur la variable (l'indice des années) conduit à un rapport (= multiplication) constant (1,04 ici) sur les images (notre A).
Autre page directement concernée : https://fr.wikipedia.org/wiki/Croissance_exponentielle :
En mathématiques, en économie et en biologie, on parle d'un phénomène à croissance exponentielle (ou géométrique) lorsque la croissance en valeur absolue de la population est proportionnelle à la population existante, c'est-à-dire lorsque le taux de croissance intrinsèque est constant et positif.
-- C'est grave une exponentielle ? --
Oui car c'est vraiment une croissance phénoménale. On a beaucoup de mal à se la représenter, et ça fascine depuis longtemps, en témoigne les histoires suivantes assez connues :
Le nénufar
Sur un lac, un nénufar a une taille qui double chaque jour. Au bout du 40ème jour il a recouvert tout le lac. Au bout de combien de jours recouvrait-il seulement la moitié du lac ?
Réponse :
L'échiquier de Sissa
https://fr.wikipedia.org/wiki/Histoire_du_jeu_d%27échecs#Le_mythe_du_brahmane_Sissa
Pour être récompensé de l'invention du jeu d'échecs, le sage Sissa demanda à recevoir une quantité de riz définie comme suit : 1 grain sur la première case, puis 2 grains sur la deuxième, 4 sur la troisième, 8 sur la quatrième, 16 sur la cinquième, et ainsi de suite en doublant à chaque fois le nombre de grains. Cela sembla raisonnable au roi qui accepta ; mais toutes les ressources du royaume n'y suffirent pas ! En effet, ça représente plus de mille fois la production mondiale de riz de 2012, ou 30 fois le PIB mondial de 2014 au prix du riz en France à ce moment là.
Conséquences et conclusion
Remarquons aussi que sur chaque case il y a à peu près autant (un de plus) de grains de riz que sur toutes les cases précédentes. Par exemple 8 c'est 1 de plus que 1 + 2 + 4. Et 16 est 1 de plus que 1 + 2 + 4 + 8.
Imaginons qu'un constructeur automobile ait une croissance de sa production qui soit égale à 5% par an. Tous les 14 ans, il va doubler sa production. Mais ça voudra aussi dire que, entre 2000 et 2014, autrement dit "une case" où la production a doublé, il aura produit autant de voitures qu'entre l'aube de l'humanité et 2000. Idem, entre 2014 et 2028, il aura produit autant de voitures que pendant toutes les années précédentes... Ça donne aussi une idée du "problème" de l'exponentielle.
On comprend donc que c'est une croissance folle. En mathématiques on n'a aucune difficulté à avoir des tels nombres, une croissance infinie etc etc. Mais dans la vraie vie, en physique, chimie, biologie... on sait que rien n'est infini, et du fait de cette croissance extrême, on va forcément atteindre des limites. Par exemple si une personne porteuse d'un virus en contamine 2, qui à leur tour en contaminent 2 (donc déjà un total de 4), ça va aller très vite : en 33 itérations (seulement ! la moitié de notre échiquier) on a dépassé nos 7 milliards d'êtres humains, tout le monde est contaminé et ça s'arrête brusquement.
Comme les ressources terrestres sont limitées, les explications ci-dessus font dire que la croissance, notamment du PIB, finira par tendre vers zéro. Ce ne sera pas "une crise parce-qu'on a pris des mauvaises décisions", mais simplement un phénomène naturel inévitable. Et ce phénomène il vaudrait mieux en tenir compte et l'anticiper car, par exemple, en basant un système de régime de retraite sur une croissance exponentielle infinie, on va aller dans le mur (c'est le cas du projet actuel du gouvernement). Et dans ce cas, la question n’est pas « est-ce ça va foirer ? », mais uniquement « quand est-ce que ça va foirer ? ».
Pour prolonger la lecture :
https://theconversation.com/face-au-mur-de-la-croissance-exponentielle-135331
https://theconversation.com/penser-lapres-les-limites-physiques-de-la-planete-138842
Pour une croissance en pourcentage p relativement faible, ce qui est le cas de la plupart des paramètres en économie, on peut estimer « la durée de la période pour doubler » avec la formule : 70 / p. Si p vaut 10%, ça prend 7 ans, si p vaut 5 ça prend 14 ans, si p vaut 1 ça prend 70 ans.
[ Dernière édition du message le 18/06/2020 à 12:33:17 ]
Dr Pouet
L'ensemble des transformations souhaitables nécessitent des investissements massifs et sauf révolution légale/économique/géopolitique qui n'arrivera pas, les capitaux ne seront pas dispo/n'existeront pas sans "croissance en valeur". Cette dernière n'ayant pas besoin d'être exponentielle.
Donc de par sa définition même (un pourcentage), soit la croissance est exponentielle, soit elle tend vers zéro.
À méditer...
dana12
Incrédule sur tout, sceptique sur le reste
Dr Pouet
L'écologie et l'économie ne sont pas vraiment copine.
Normalement, à l'origine, l'économie c'est pour... roulement de tambour... être économe ! Ou plus exactement : "gérer au mieux les ressources qui ne sont disponibles qu'en quantités limitées, et étudier comment on peut faire ça".
En fait c'est plutôt la finance et surtout l'appât du gain sans limite qui sont problématiques. En plus il faut bien voir qu'en cas de désaccord, c'est évidemment les lois de la nature qui auront le dernier mot et seront les plus fortes.
Beaucoup de thèses économiques actuelles sont incomplètes, voire complètement fausses, souvent pour complaire aux financiers et aux politiciens. Exemple d'erreur qui fait que c'était bien mal parti : pour Jean-Baptiste Say (l'un des premiers économistes), il était inutile de prendre en compte l'énergie parmi les paramètres économiques. En effet, celle-ci semblait gratuite et disponible en quantité illimitée... ben oui, le vent pour les moulins ou les bateaux, ou le débit d'une rivière pour les moulins, étaient disponibles à foison. Mais on a oublié cette approximation en passant au charbon, pétrole, gaz, nucléaire...
Le polytechnicien économiste Charles Dupin (qui a peut-être aussi inspiré un célèbre personnage de Poe, peut-être le premier détective), n'avait pas commis cette erreur en recensant et comparant le nombre de moulins et bateaux entre la France et l'Angleterre (et donc en gros, la puissance en Watts des deux nations).
Les économistes prennent également rarement en compte les baisses de production agricoles liées à la pollution (au sens large : trucs toxiques, mais aussi mort des insectes pollinisateurs, bouleversement climatique à cause du CO2...). Et ils ne s'intéressent pas trop aux problèmes de pénuries d'énergie à long terme (comme si on ne faisait pas de bilan comptable
Pourtant dans des simulations comme celle du "Club de Rome", il y a de quoi s'alarmer ! Bien sûr les quantités et donc les dates de cette simulation sont très approximatives, mais même en les faisant beaucoup varier, ça donne à peu près toujours les mêmes solutions. Donc il y a de quoi s'inquiéter fortement. Surtout que leurs prévisions, faites dans les années 70, sont en train de se confirmer, et ce n’est pas pour le meilleur...
Et quand je vois que pendant des années de cours d'économie au lycée ou après (mais ce n'était pas une matière dominante pour moi), je n'ai jamais entendu un professeur souligner qu'une croissance annuelle en pourcent est une croissance exponentielle, c'est fou ! Or une croissance exponentielle, en dehors des mathématiques, dans la vie réelle, ça s'arrête toujours, donc à minima il vaudrait mieux se soucier très sérieusement de ce problème.
[ Dernière édition du message le 19/06/2020 à 20:22:09 ]
Dr Pouet
Donc de par sa définition même (un pourcentage), soit la croissance est exponentielle, soit elle tend vers zéro.
Cette affirmation peut paraître un peu audacieuse, mais en fait sa justification est très simple.
Imaginons que la croissance ne tende pas vers zéro. Alors dans ce cas ça veut dire qu'elle est toujours supérieure à un pourcentage P, strictement supérieur à zéro. Mais du coup ça veut aussi dire qu'elle est toujours supérieure à notre A défini 4 messages au-dessus, en remplaçant 1,04 par (1 + P / 100). Et comme A a une évolution exponentielle...
Le souci c'est que pas mal de choses sont basées sur la croissance du PIB, et que si cette dernière est plus faible que prévu, on va avoir un problème. Tant que c'est le compte épargne de Bernard Arnault, ce n'est pa très grave, mais quand ce sont nos retraites, c'est plus ennuyeux.
Et pour reprendre les calculs ci-dessus, avec une croissance du PIB de 2% comme ces dernières années, ce PIB double tous les 35 ans. Quand Bruno Le Maire croit possible une croissance de 6%, il croit à un PIB qui double tous les 12 ans. Ça veut dire qu'en seulement 12 ans, on produit autant de biens et services que pendant toutes les années et tous les siècles précédents.
- < Liste des sujets
- Charte