Sujet L'Orgue à tuyaux et l'Organiste
- 2 916 réponses
- 85 participants
- 168 563 vues
- 82 followers
Afficher le sujet de la discussion
sonicsnap
83686
AF, je suis ton père
Membre depuis 18 ans
darinze
4536
Squatteur·euse d’AF
Membre depuis 3 ans
alex.d.
5498
Je poste, donc je suis
Membre depuis 9 ans
sonicsnap
83686
AF, je suis ton père
Membre depuis 18 ans
darinze
4536
Squatteur·euse d’AF
Membre depuis 3 ans
Plongeons au coeur de la physique, des maths et de la mécanique des fluides!
Nous allons chercher à calculer la longueur du pied acoustique.
Rappelez-vous: cette unité permet d'exprimer la longueur des tuyaux, et conséquemment la hauteur de la note qu'ils produisent.
On nomme les jeux selon leur timbre, et on fait suivre un nombre de pieds, qui situe la hauteur à laquelle ils parlent. On a donc par exemple la flûte 8, le prestant 4, la doublette 2, le bourdon 16, la contre-bombarde 32... et puis des exotiques comme le nazard 2'2/3, ou la tierce 1'3/5.
Ce nombre équivaut à la longueur du tuyau le plus long du jeu, en général c'est un DO.
Les jeux de 8 pieds sont à la hauteur de la voix de l'homme. Les 4 pieds sont une octave plus aigus. Les 2 pieds sont une octave plus aigus que les 4, donc deux octaves plus aigus que les 8. Les 16 pieds sont une octave plus graves que les 8. Etc.
J'ai indiqué péremptoirement au début de ce topic que le pied acoustique fait 0.324m.
Le tuyau d'un DO grave de 8 pieds mesure donc 8*0.324 = 2.59m de long. Le DO grave d'un jeu de 4 pieds mesure la moitié de cette longueur, soit 4*0.324 = 1.30m.
La question qu'on se pose est: comment arrive-t-on cette longueur de 0.324?
Pour cela, il est nécessaire de comprendre ce qu'il se passe à l'intérieur du tuyau lorsqu'il fait entendre une note.
Arrêtons le temps à la Matrix, au moment précis où l'organiste appuie sur la touche. Le mouvement déclenche une soupape qui permet à l'air sous pression d'entrer dans le tuyau. Avançons petit à petit.
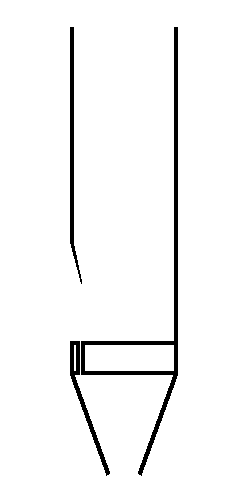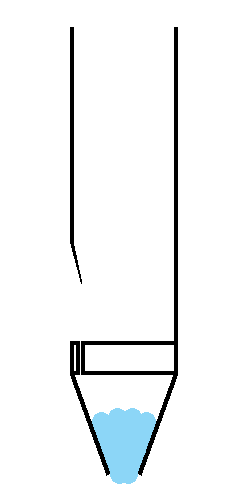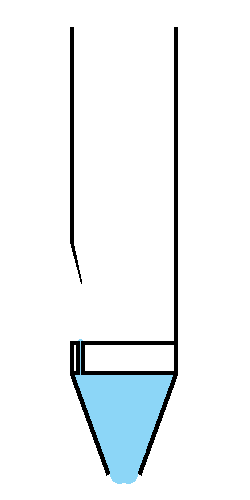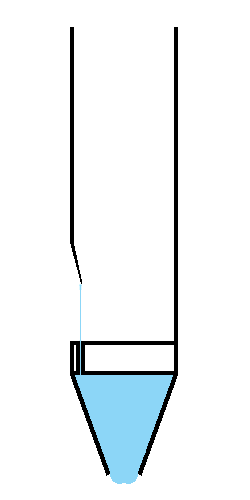
L'air s'engouffre par le pied, et il est canalisé en une fine lame sur le biseau, contre lequel il se divise.
C'est là que tout se joue, car le flux d'air n'est pas régulier dans sa division.
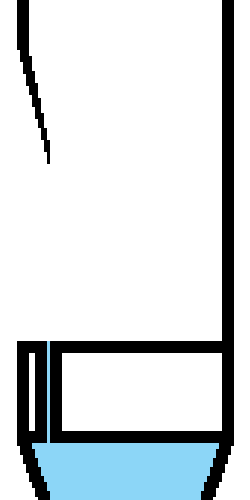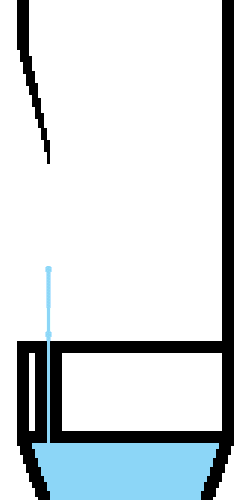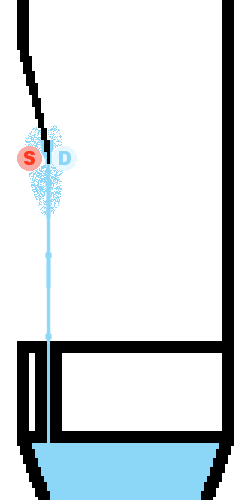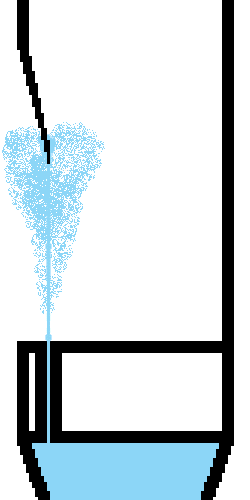
Dans un tout premier temps, il va s'échapper par l'extérieur, mais l'air ambiant agit comme un coussin et lui oppose une résistance. Une surpression (S) se forme, et donc une dépression (D) se forme en réponse, à l'intérieur du corps du tuyau.
Cette surpression et la dépression conjointes provoquent une inversion des flux, et l'air est alors attiré vers l'intérieur du tuyau. Ce qui crée maintenant une surpression dans le corps, alliée à une dépression qui lui répond à l'extérieur, aidée par l'effet coussin de l'air ambiant.
Tant qu'il est alimenté, le flux d'air oscille ainsi indéfiniment autour du biseau, passant alternativement de l'intérieur à l'extérieur du tuyau, et générant autant de situations de surpression et dépression qui échangent sans arrêt leur place.
La division du flux d'air ne peut pas être stable, et de cette instabilité naît le son.
Ralentissons à nouveau le temps, au moment précis où, dans l'oscillation du flux d'air précédente, une surpression se crée à l'intérieur du tuyau.
Cette surpression génère une onde, qui va se propager à l'intérieur du tuyau, à la vitesse du son.
Arrivée à l'autre extrémité du tuyau, elle rencontre le coussin d'air ambiant, qui lui oppose une certaine résistance. Une partie de son énergie génère une onde, qui s'échappe par le haut du tuyau dans l'air ambiant, tandis que le reste repart et parcourt à nouveau le tuyau en sens inverse. Arrivé en bas, l'onde va être réfléchie par la paroi qui forme le pied du tuyau. Elle repart alors à nouveau en sens inverse, et reparcourt le tuyau jusqu'au sommet, où le même phénomène va se reproduire : une onde sera émise dans l'air ambiant, tandis qu'une nouvelle onde résiduelle repartira vers la base, et ainsi de suite.
Ce mouvement se répète jusqu'à ce que l'énergie initiale soit complètement amortie.
Lorsqu'on libère le temps et qu'on considère l'émission d'une note sur plusieurs secondes, l'oscillation incessante du flux d'air autour du biseau, vue précédemment, génère en continu des surpressions, donc alimente en continu ce mouvement que nous venons de voir en détail, générant en continu des ondes dans l'air ambiant à une fréquence toujours constante.
Comme l'onde interne se déplace à vitesse constante (celle du son) dans une longueur constante (celle du tuyau), l'onde générée au sommet du tuyau s'échappe dans l'air ambiant à une fréquence régulière. La régularité de cette émission est à l'origine de la "note" que nos oreilles perçoivent.
Passons aux maths.
La fréquence, F, est le nombre de fois par seconde où une onde sera émise dans l'air ambiant. Elle est directement liée à la note qu'on entend.
La longueur, L, est celle du corps du tuyau.
La vitesse, V, est celle du son.
L'onde à l'intérieur du tuyau doit parcourir 2 fois la longueur du tuyau pour générer 1 onde dans l'air ambiant : une fois en montant, une fois en descendant.
Comme la fréquence est F, cela signifie qu'en 1 seconde, cette distance est parcourue F fois.
Par ailleurs, l'onde se déplace à la vitesse du son, donc en 1 seconde elle parcourt V.
Donc 2*L*F = V
Donc L = V / 2F
Si l'on se base sur un LA=440Hz, le DO de 1 pied a une fréquence de 523.25 Hz.
On estime couramment la vitesse du son V=340 m/s.
La longueur du tuyau de 1 pied est donc L = V/2F = 340 / (2 * 523.25) = 0.32489
Bien sûr, ce calcul est arbitraire, puisque j'ai choisi arbitrairement une vitesse du son et une fréquence de référence. Au cours des siècles, les facteurs d'orgues n'ont pas observé le même diapason de référence. L'orgue de Saint Maximin dans le Var est ainsi quasiment un ton plus bas que le LA 440.
Nous allons chercher à calculer la longueur du pied acoustique.
Rappelez-vous: cette unité permet d'exprimer la longueur des tuyaux, et conséquemment la hauteur de la note qu'ils produisent.
On nomme les jeux selon leur timbre, et on fait suivre un nombre de pieds, qui situe la hauteur à laquelle ils parlent. On a donc par exemple la flûte 8, le prestant 4, la doublette 2, le bourdon 16, la contre-bombarde 32... et puis des exotiques comme le nazard 2'2/3, ou la tierce 1'3/5.
Ce nombre équivaut à la longueur du tuyau le plus long du jeu, en général c'est un DO.
Les jeux de 8 pieds sont à la hauteur de la voix de l'homme. Les 4 pieds sont une octave plus aigus. Les 2 pieds sont une octave plus aigus que les 4, donc deux octaves plus aigus que les 8. Les 16 pieds sont une octave plus graves que les 8. Etc.
J'ai indiqué péremptoirement au début de ce topic que le pied acoustique fait 0.324m.
Le tuyau d'un DO grave de 8 pieds mesure donc 8*0.324 = 2.59m de long. Le DO grave d'un jeu de 4 pieds mesure la moitié de cette longueur, soit 4*0.324 = 1.30m.
La question qu'on se pose est: comment arrive-t-on cette longueur de 0.324?
Pour cela, il est nécessaire de comprendre ce qu'il se passe à l'intérieur du tuyau lorsqu'il fait entendre une note.
Arrêtons le temps à la Matrix, au moment précis où l'organiste appuie sur la touche. Le mouvement déclenche une soupape qui permet à l'air sous pression d'entrer dans le tuyau. Avançons petit à petit.
L'air s'engouffre par le pied, et il est canalisé en une fine lame sur le biseau, contre lequel il se divise.
C'est là que tout se joue, car le flux d'air n'est pas régulier dans sa division.
Dans un tout premier temps, il va s'échapper par l'extérieur, mais l'air ambiant agit comme un coussin et lui oppose une résistance. Une surpression (S) se forme, et donc une dépression (D) se forme en réponse, à l'intérieur du corps du tuyau.
Cette surpression et la dépression conjointes provoquent une inversion des flux, et l'air est alors attiré vers l'intérieur du tuyau. Ce qui crée maintenant une surpression dans le corps, alliée à une dépression qui lui répond à l'extérieur, aidée par l'effet coussin de l'air ambiant.
Tant qu'il est alimenté, le flux d'air oscille ainsi indéfiniment autour du biseau, passant alternativement de l'intérieur à l'extérieur du tuyau, et générant autant de situations de surpression et dépression qui échangent sans arrêt leur place.
La division du flux d'air ne peut pas être stable, et de cette instabilité naît le son.
Ralentissons à nouveau le temps, au moment précis où, dans l'oscillation du flux d'air précédente, une surpression se crée à l'intérieur du tuyau.
Cette surpression génère une onde, qui va se propager à l'intérieur du tuyau, à la vitesse du son.
Arrivée à l'autre extrémité du tuyau, elle rencontre le coussin d'air ambiant, qui lui oppose une certaine résistance. Une partie de son énergie génère une onde, qui s'échappe par le haut du tuyau dans l'air ambiant, tandis que le reste repart et parcourt à nouveau le tuyau en sens inverse. Arrivé en bas, l'onde va être réfléchie par la paroi qui forme le pied du tuyau. Elle repart alors à nouveau en sens inverse, et reparcourt le tuyau jusqu'au sommet, où le même phénomène va se reproduire : une onde sera émise dans l'air ambiant, tandis qu'une nouvelle onde résiduelle repartira vers la base, et ainsi de suite.
Ce mouvement se répète jusqu'à ce que l'énergie initiale soit complètement amortie.
Lorsqu'on libère le temps et qu'on considère l'émission d'une note sur plusieurs secondes, l'oscillation incessante du flux d'air autour du biseau, vue précédemment, génère en continu des surpressions, donc alimente en continu ce mouvement que nous venons de voir en détail, générant en continu des ondes dans l'air ambiant à une fréquence toujours constante.
Comme l'onde interne se déplace à vitesse constante (celle du son) dans une longueur constante (celle du tuyau), l'onde générée au sommet du tuyau s'échappe dans l'air ambiant à une fréquence régulière. La régularité de cette émission est à l'origine de la "note" que nos oreilles perçoivent.
Passons aux maths.
La fréquence, F, est le nombre de fois par seconde où une onde sera émise dans l'air ambiant. Elle est directement liée à la note qu'on entend.
La longueur, L, est celle du corps du tuyau.
La vitesse, V, est celle du son.
L'onde à l'intérieur du tuyau doit parcourir 2 fois la longueur du tuyau pour générer 1 onde dans l'air ambiant : une fois en montant, une fois en descendant.
Comme la fréquence est F, cela signifie qu'en 1 seconde, cette distance est parcourue F fois.
Par ailleurs, l'onde se déplace à la vitesse du son, donc en 1 seconde elle parcourt V.
Donc 2*L*F = V
Donc L = V / 2F
Si l'on se base sur un LA=440Hz, le DO de 1 pied a une fréquence de 523.25 Hz.
On estime couramment la vitesse du son V=340 m/s.
La longueur du tuyau de 1 pied est donc L = V/2F = 340 / (2 * 523.25) = 0.32489
Bien sûr, ce calcul est arbitraire, puisque j'ai choisi arbitrairement une vitesse du son et une fréquence de référence. Au cours des siècles, les facteurs d'orgues n'ont pas observé le même diapason de référence. L'orgue de Saint Maximin dans le Var est ainsi quasiment un ton plus bas que le LA 440.
T'es pas obligé d'écouter toutes les conneries de DaRinze.
[ Dernière édition du message le 02/12/2021 à 22:06:11 ]
kosmix
45609
Ma vie est un thread...
Membre depuis 19 ans
Bravo c'est fascinant 
Mention spéciale pour les gifs d'illustration
Mention spéciale pour les gifs d'illustration
Putain Walter mais qu'est-ce que le Vietnam vient foutre là-dedans ?
[ Dernière édition du message le 03/12/2021 à 00:50:05 ]
MaiMai
1772
AFicionado·a
Membre depuis 14 ans
Heureux de suivre encore ce super topic sur L'Orgue à tuyaux !
Merci darinze pour ce beau travail et de le partager.
Merci darinze pour ce beau travail et de le partager.
moi, j'ai pas d'blé mais j'ai du son...
darinze
4536
Squatteur·euse d’AF
Membre depuis 3 ans
Oui désolé pour l'à peu près des GIF. J'ai un peu galéré pour modéliser les volutes d'air 
T'es pas obligé d'écouter toutes les conneries de DaRinze.
Desmodue
5171
Je poste, donc je suis
Membre depuis 19 ans
Voilà que ce forum reprend du poil de la bête !
darinze
4536
Squatteur·euse d’AF
Membre depuis 3 ans
Merci 
Au passage, puisque L = V / 2F, c'est ce qui explique que le tuyau diminue de moitié de longueur lorsque la fréquence double, c'est-à-dire lorsqu'on passe à l'octave supérieure.
Et inversement, que le tuyau double de longueur quand on divise la fréquence par deux, c'est-à-dire lorsqu'on passe à l'octave inférieure.
Au passage, puisque L = V / 2F, c'est ce qui explique que le tuyau diminue de moitié de longueur lorsque la fréquence double, c'est-à-dire lorsqu'on passe à l'octave supérieure.
Et inversement, que le tuyau double de longueur quand on divise la fréquence par deux, c'est-à-dire lorsqu'on passe à l'octave inférieure.
T'es pas obligé d'écouter toutes les conneries de DaRinze.
- < Liste des sujets
- Charte