Savoir ce qu’une enceinte peut accepter comme puissance électrique ne nous informe pas sur le niveau sonore qu’on aura.
Une certaine partie de l’énergie du signal va être dissipée sur le chemin jusqu’à l’air. Dans un haut-parleur classique, le signal fait bouger la bobine mobile dans un champ magnétique et ce mouvement entraîne un diaphragme qui met l’air en pression. Malheureusement une bonne partie de l’énergie disparaît en chaleur dans la bobine et les aimants. La conversion de l’énergie électrique en énergie mécanique, puis en énergie acoustique se fait au prix de pertes plus ou moins importantes, selon les haut-parleurs et les enceintes dans lesquelles ils sont montés. Ainsi pour comparer deux enceintes entre elles, il est intéressant de voir quelle pression acoustique elles fournissent pour une puissance électrique donnée.
Définitions de la sensibilité et du rendement
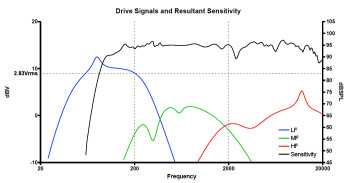
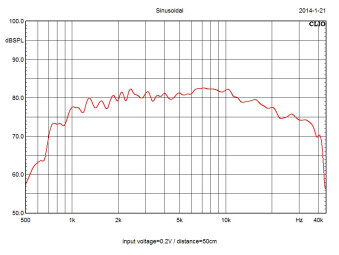
La sensibilité indique le niveau sonore qu’une enceinte peut délivrer, en conditions de test, en fonction de la puissance qu’elle reçoit. On note la sensibilité en décibels de pression acoustique (dB SPL) pour 1 watt (ou 2,83 volts, voir plus bas) à 1 mètre dans l’axe.
La notion de rendement est conceptuellement proche : il exprime le rapport entre l’énergie sonore délivrée et l’énergie électrique reçue, en pourcentage ou en ratio (10 % correspond à un ratio de 0,1). Le rendement pour la majorité des enceintes est en dessous de 5 %. L’air résiste plutôt bien au travail des haut-parleurs.
Sachant qu’en doublant la puissance électrique du signal, le niveau sonore augmente de 3 dB SPL, une enceinte amplifiée par 100 W de puissance avec une sensibilité de 92 dB/1 W @ 1 m aura un niveau sonore équivalent à une enceinte amplifiée par 50 W avec une sensibilité de 95 dB/1 W @ 1 m. On voit bien que la puissance admissible d’une enceinte, sans sa sensibilité, ne permet pas de juger du volume qu’il y aura en sortie. Par contre avec les deux, on peut évaluer le niveau maximum qu’on pourra théoriquement obtenir.
Pourquoi 2,83 V ?
La puissance (en watts) est dépendante de l’impédance, et l’impédance change en fonction de la fréquence. Pour maintenir une puissance de 1 watt pour le test, il faudrait ajuster la tension du signal en fonction de l’enceinte et de la plage de fréquence testées. Pour faciliter le test, on préfère que les variables soient du côté de l’enceinte à tester, pas dans le signal. Donc au lieu de caractériser le signal test par sa puissance (1 W), qui de toute manière n’est qu’un calcul à partir de sa tension, on préfère lui donner une valeur de tension fixe (2,83 V) et mesurer ce que chaque enceinte fournit comme pression acoustique avec.
La relation entre la puissance (P) et l’impédance (Z) s’exprime par la formule P = U2/Z. Avec 2,83 V et une impédance de 8 Ω, on obtient 2,832 V/8 Ω = 1 W. Pour 4 Ω : 2,83 V donnent 2 W. En conséquence, une enceinte avec une impédance nominale de 4 Ω sera plus efficace si elle est capable de délivrer 92 dB/1 W @ 1 m que si elle donne 92 dB/2,83 V @ 1 m (elle reçoit 2 W dans ce cas là). Cela dit, on peut s’attendre à ce que la notation en 2,83 V « favorise » les enceintes de 4 Ω ; elles recevront une puissance électrique supérieure aux enceintes de 8 Ω, à tension égale. L’impédance est indispensable à regarder en complément de la forme x dB/2,83 V @ 1 m. La plus grande rigueur logique de cette notation la fait préférer à celle en watts, mais, on le voit, il y a des équivalences entre les deux.
Niveau max SPL
De temps en temps, sur les spécifications d’une enceinte, il est fait mention d’un niveau maximum de pression acoustique en dB SPL. C’est le niveau sonore de crête obtenu avec la puissance de crête de l’amplification (telle que spécifiée par le constructeur). On peut le calculer si on a la sensibilité de l’enceinte et la puissance d’ampli utilisée. Il est souvent donné pour faciliter la modélisation d’un système en situation réelle. Avec ce chiffre et une connaissance des échelles en décibels, c’est assez simple de calculer quelle pression acoustique on aura (en théorie), en fonction de la distance de l’enceinte. On estime, en simplifiant, qu’on perd 6 dB lorsqu’on double la distance à la source (cas d’une onde sphérique). Donc en fonction de la distance de l’auditeur par rapport à l’enceinte, on peut calculer le niveau sonore maximum théorique auquel il sera soumis.
**Atténuation, en décibels, en fonction de la distance de la source, en mètre.