Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
Notifications
< Retour vers Bidouille & Développement Informatique
Agrandir
Bidouille & Développement Informatique
Les Mains dans le Cambouis
Bidouille & Développement Informatique
Actu 1 1
Articles
Médias 33 33
Tutoriels
Forums 326 326

Outil d'évaluation du taux de distorsion d'un équipement audio

  • 17 réponses
  • 7 participants
  • 1 666 vues
  • 6 followers
Sujet de la discussion Outil d'évaluation du taux de distorsion d'un équipement audio
Bonjour à tous,

petit outil ajouté sur mon site sonelec-musique : AudioDistMeas, qui permet d'évaluer la distorsion causée par un équipement audio.

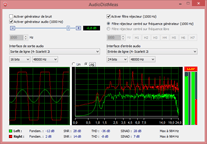
audiodistmeas_main_001_tn.gif

AudioDistMeas

Cela faisait un moment que j'avais ce truc en tête, pour agrémenter mes cours sur les défauts sonores. Et quelqu'un m'a récemment demandé si je n'avais pas dans un coin de mon labo virtuel, un soft simple qui intégrait générateur BF et analyseur de spectre, pour ajuster au plus bas le taux de distorsion d'un de ses équipement DIY. Voilà qui est fait ;-)

Petite remarque/limitation : les valeurs affichées de SNR, THD et SINAD ne sont pas encore au point. Cela n'empêche pas le logiciel d'être fonctionnel.

Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com

Afficher le sujet de la discussion
11
Bonjour Phil, et merci.
Oui cela est très juste, mon avertissement va dans ce sens, c'est pourquoi je décris ce soft comme un outil d'évaluation. Il va de soi que si le plancher de bruit est à -50dBFS, on ne pourra pas aller très loin ;-)

Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com

12
Salut,

Citation de chimimic :
J'ai tatonné pas mal de temps avec les filtres pour obtenir une forte réjection du 1000 Hz tout en conservant une atténuation faible ou nulle à 2000 Hz et au-delà.
C'est une solution très "hardware" du problème ; pourquoi ne pas utiliser une méthode haute résolution ?
- Il n'y a pas de filtre à régler ;
- Le niveau de bruit perturbe très peu l'évaluation des harmoniques.

Je ne sais pas si tu les connais déjà ; les méthodes d'analyses spectrales HR ont souvent mauvaise presse parce qu'elles sont (trop) souvent mal utilisées.
En général il s'agit d'ajuster les paramètres d'un modèle paramétrique du signal d'intérêt à partir d'une mesure. Quand le modèle ne correspond pas au signal la méthode échoue lamentablement (normal).
En revanche, lorsque le modèle est bien adapté et que l'algorithme d'estimation des paramètres est assez robuste, les méthodes HR sont très efficaces ; la connaissance a priori du modèle de signal permet à la fois de rejeter le bruit et de descendre en dessous de la limite de résolution en fréquence imposée par la taille de la fenêtre temporelle.

La partie compliquée des algo HR avec modèle sinusoïdes harmoniques est l'estimation des pulsations propres or tu n'en as pas besoin. Dans ton cas tu injectes une sinusoïde test dont tu maîtrises la fréquence F et tu récupères une somme de sinusoïdes de fréquences multiples de F avec un éventuel déphasage et un bruit additif (bien sûr, il y a plus, mais c'est déjà un bon point de départ).

x(t) = ∑ a_i*sin(i*ω*t + φ_i) + b(t)
avec i allant de 1 à P où P est l'ordre du modèle et b(t) le bruit additif.

Pour chaque composante :
a_i*sin(i*ω*t + φ_i) = a_i*cos(φ_i)*sin(i*ω*t) + a_i*sin(φ_i)*cos(i*ω*t)

En notant c_i := a_i*cos(φ_i) et s_i := a_i*sin(φ_i) :
x(t) = [ ∑ c_i*sin(i*ω*t) + s_i*cos(i*ω*t) ] + b(t)

x(t) c'est ce que l'on mesure.

ω = 2*π*F est connue : C'est la pulsation de la sinusoïde de test (en supposant que les horloges des CNA/CAN sont synchrones ou dérivent peu l'une par rapport à l'autre).

Les paramètres à estimer sont les c_i et s_i. On retrouve ensuite :
a_i = √(c_i² + s_i²)
φ_i = atan(s_i/c_i)


L'intérêt du développement trigonométrique est que l'on a linéarisé le problème (on aurait aussi pu passer par les amplitudes complexes). En posant :
A = [ s_1 s_2 ... s_P s_1 c_2 ... c_P ]' (un vecteur colonne)
S(t) = [ cos(ω*t) cos(2*ω*t) ... cos(P*ω*t) sin(ω*t) sin(2*ω*t) ... sin(P*ω*t) ] (un vecteur ligne)

On a directement :
x(t) = S(t) * A + b(t) (avec * le produit matriciel)

En indexant par n les échantillons du signal numérisé (t = n*Te = n/Fe) :
x(0) = S(0) * A + b(0)
x(1) = S(1) * A + b(1)
...
x(N) = S(N) * A + b(N)

En posant :
- X le vecteur colonne contenant les N+1 échantillons du signal mesuré ;
- M la matrice qui emplie des S(n) (que l'on calcule à partir de ω connue) ;
- B le vecteur des échantillons du bruit additif.

==> X = M*A + B

Je n'ai (malheureusement) pas utilisé les mêmes notations mais il s'agit ni plus ni moins d'un cas qui se résout classiquement avec les moindres carrés :
https://fr.wikipedia.org/wiki/M%C3%A9thode_des_moindres_carr%C3%A9s#.C3.89quations_normales des moindre carré
Avec la méthode de pseudo inversion on obtient l'estimation optimale au sens des moindres carrés :
==> A_est = (M'*M)^-1 * M' * X

Où M' est la transposée de M et ^-1 l'inversion matricielle.

A partir de A_est on peut calculer l'amplitude de chaque composante harmonique, et donc les puissances de chaque composante, le THD, etc.

X_est = M*A_est est la version débruitée du vecteur de mesure X ; en calculant X - M*A_est = B_est on obtient l'estimation du signal de bruit additif, dont on peut calculer la puissance puis tout ce qui vient avec (SNR, THD+N, etc.).

Comme tu peux le constater, le gros intérêt de la méthode c'est que l'estimation écarte le bruit en le séparant du signal (c'est la méthode "en sous-espaces signal/bruit") et l'on n'a pas altéré le signal de mesure avec un filtre (il n'y a pas besoin d'un filtre bouchon puisque l'on a directement accès à chaque amplitude).


Au niveau des limitations :
- Si le bruit est trop loin du bruit additif "normal" (du moins unimodal) et que la mesure est entachée de points aberrants la méthode des moindres carrées va se planter et dévier... mais la mesure "classique" avec filtre aussi. Une solution est d'utiliser un estimateur robuste (mais c'est plus compliqué) ; dans la vraie vie on refait simplement la mesure ;
- Si la valeur de ω (ou F) n'est pas la bonne, la méthode dévisse complètement. De ce point de vue là ça sera assez binaire : Soit ω est ok et ça marche très bien, soit ω est ko et ça ne marche pas du tout.

Pour se dernier point, si c'est l'outil qui génère la sinusoïde de teste il n'y a pas de raison que cela arrive, sinon c'est que l'on a un souci de génération / mesure.
Avec un générateur extérieur on risque d'avoir un léger écart et là, la méthode proposée ne suffit plus : Il faut alors faire précéder l'évaluation de la pulsation propre du signal. Ça se fait sans problème mais l'algo est d'un autre niveau de complexité...


D'un point de vue réglage :
Il faut uniquement choisir l'ordre du modèle (le nombre d'harmoniques). La méthode bourrin consiste à choisir P de manière à couvrir toute la bande passante : P = E(Fe/(2*F)).
D'un point de vue puissance de calcul ça passe généralement... (comparé à une FFT et si l'on implémente astucieusement l'inversion matricielle, ce n'est pas grand chose) ; mais on risque tout de même d'ajuster des harmoniques sur le bruit de fond. Pas de danger de biaiser la mesure parce que la puissance (discrète) de ces sinusoïdes est très faible et elles peuvent être rejetées a posteriori.
Autre méthode : Si l'on dispose déjà d'une FFT on compte le nombre de pics qui dépassent le plafond de bruit.


D'un point de vue implémentation :
A_est = (M'*M)^-1 * M' * X

- X c'est la fenêtre (non pondérée) des échantillons mesurées ;
- M la matrice des sin(i*ω*n/Fe), cos(i*ω*n/Fe).
- Le gros morceau c'est l'inversion matricielle (M'*M)^-1.

Pour commencer à se rassurer, l'inversion porte sur M'*M qui est une matrice PxP (P ordre du modèle) et non NxN (nombre d'échantillons) avec P << N même si l'on choisi la méthode bourrin pour P.
Ensuite on peut réaliser une décomposition QR préliminaire de M (algo largement documenté) :
https://fr.wikipedia.org/wiki/D%C3%A9composition_QR

M = Q*R
=> M'*M = (Q*R)'*(Q*R) = R'*Q'*Q*R = R'*Id*R = R'*R
=> (M'*M)^-1 = (R'*R)^-1

En retirant les lignes de 0 inutiles de R (en tout cas pour le calcul de R'*R), on obtient une matrice carrée triangulaire inversible (il faut s'assurer qu'il n'y a pas de 0 sur la diagonale principale) :
(M'*M)^-1 = R^-1 * (R^-1)'

Et comme R est triangulaire, on peut calculer le vecteur résultat y = R^-1 * x connaissant le vecteur colonne x par substitution sans passer explicitement par l'inversion matricielle de R (idem pour R').
A_est = (M'*M)^-1 * M' * X = R^-1 * ((R^-1)' * (M' * X))

En commençant par la droite, obtient alors 3 produits successifs d'une matrice et d'un vecteur colonne.

Citation de chimimic :
Il va de soi que si le plancher de bruit est à -50dBFS, on ne pourra pas aller très loin
Avec la méthode HR ça s'encaisse ; le vrai problème restant devient les distorsions des convertisseurs.

[ Dernière édition du message le 07/08/2016 à 13:37:39 ]

13
Bonjour EraTom,

wow, un grand merci pour toutes ces explications extrêmement bien détaillées !

J'ai bien peur de n'avoir pas à ce jour la compétence nécessaire pour saisir tout cela comme il se doit, mais je garde ton intervention bien au chaud. De toute évidence cela me servira quand cet "outil d'évaluation" deviendra un "outil de mesure".

:D:

Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com

14
Si tu veux creuser ce genre d'algo et discuter de l'implémentation pour voir ce que ça donne on peut échanger.

Perso je me contente de Matlab parce que je n'ai pas de besoin temps réel... Et puis surtout parce que la partie codage des interfaces etc. me gonfle.
Ceci dit, je code quelques fonctions bas niveaux en C# (qui s'intègrent facilement dans Matlab) parce que les lib BLAS et LAPACK ne proposent pas toujours ce que je souhaite (par exemple, la sommation de Kahan qui limite l'accumulation d'erreurs d'arrondi n'est pas incluse dans BLAS).
15
Pour ma part, coder des interfaces me plaît assez. Mais la majorité des algos de filtrage sont encore pour moi, du chinois. Je me documente et fais quelques tests de temps à autres, en fonction des besoins du jour. Je ne suis nullement spécialiste du sujet mais comme on dit, j'ai une "petite base". Les cours sur le filtrage numérique que j'ai suivis à l'INA il y a trente ans me gonflaient, je n'y comprenais rien ! A ce jour, j'utilise des bibliothèques toutes faites, tout simplement parce que je manque de temps pour tout développer en repartant de zéro. Ce serait idiot de toute façon, autant utiliser ce qui existe. Et garder son temps dispo pour en comprendre les grandes lignes...
J'apprécie ton aide/soutien.

Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com

16
Citation :
Ce serait idiot de toute façon, autant utiliser ce qui existe.
Oui tu as raison, mais il faut faire attention car dans ce qui existe pour l'audio il y a trop souvent des choses à éviter (et le numérique en rajoute une couche).

Enfin j'enfonce des portes ouvertes...
17
;)

Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com

18
Flag !
Merci pour le développement :) :)

Chris Kazvon

-------------------------------------------------

Introduction à Hornresp et Tutoriels  -  Tutoriels Vidéo pour Room EQ Wizard