Sujet Questions de physique acoustique 101
- 3 réponses
- 3 participants
- 762 vues
- 5 followers
Sardino
73
Posteur·euse AFfranchi·e
Membre depuis 6 ans
Bonjour à tous,
Je crée ici un post car je me penche sur la physique acoustique pour essayer de construire au mieux une cabine dans laquelle je puisse jouer dans mon appartement. Je suis en train de m'y mettre grâce à ce cours très clair : http://www.ac-grenoble.fr/lycee/roger.deschaux/documents/Cours/Acoustique/Acoustique-Cours_1.pdf
J'essaye d'organiser ce post de manière cohérente.
PREMIÈRE QUESTION
Je joue du saxophone ténor. La note la plus grave (Bb, Ab en ut) semble descendre assez bas dans le spectre des fréquences. Je vous mets ici une illustration.
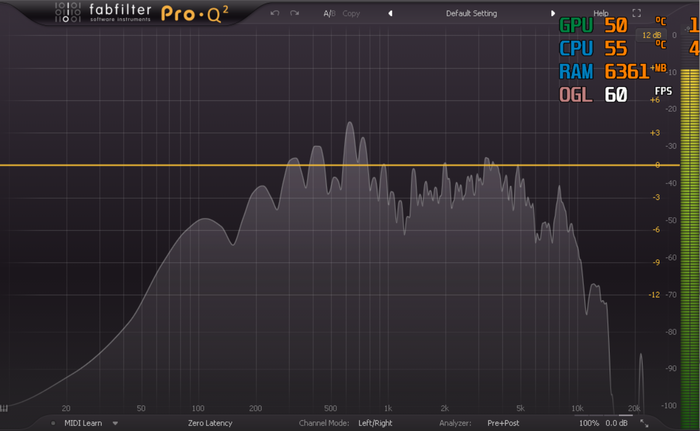
Il faut donc construire une cabine qui ait une fréquence de résonance qui soit plus basse que celles du saxophone dans sa note la plus grave, donc, en gros il faut que la fréquence de résonance de la cabine soit en dessous de 100Hz.
Je ne peux pas faire de cloison trop épaisses pour la cabine, je suis parti sur 15 cm maximum, avec 10 cm de vide d'air (ou avec laine de roche) maximum.
J'ai appliqué la formule suivante : fr (fréquence de résonance) = 84 √(1/d)*((1/m1) + (1/m2)), d étant le vide d'air (en mètre) et m1 et m2 la masse surfacique des deux parois désolidarisées de la cabine.
Je pars sur deux matériaux différents pour les deux parois, pour éviter qu'ils aient la même fréquence critique. J'ai donc fait des test avec une plaque de BA13 phonique, de masse surfacique de 11.2kg/m² ; et une plaque de BA18, de masse surfacique de 16.8kg/m².
Voici les résultats.
- Avec un vide d'air de 6 cm, la fréquence de résonance de la cabine est de 132Hrz .
- avec un vide d'air de 8 cm, la fréquence de résonance de la cabine est de 114.5Hrz
- avec un vide d'air de 9 cm la fréquence de résonance est de 108Hrz
- avec un vide d'air de 10cm, la fréquence de résonance est de 102Hrz.
J'ai essayé de remplacer le BA18 par du BA25, de masse surfacique de 18.3kg/m²:
- avec un vide d'air de 6 cm, la fréquence de résonance de la cabine est de 130Hrz.
- avec un vide d'air de 8cm, la fréquence de résonance de la cabine est de 112Hrz.
J'ai été choqué par le peu de différence que le changement d'épaisseur du placo produisait sur la fréquence de résonance de l'ensemble de la cabine.
Quoi qu'il en soit, tous ces résultats sont insatisfaisants, et la cabine risque de résonner quand je joue dans les graves, ce qui serait contre-productif, pire encore que de jouer sans cabine.
Quelqu'un connaîtrait-il une équation miracle pour réduire la fréquence de résonance de la cabine(une savant combinaison de deux masses surfaciques spécifiques peut-être ?) ou bien la seule solution est-ce d'accroitre le vide d'air ?
DEUXIÈME QUESTION
Comment peut-on connaître la fréquence critique des différents matériaux (c'est-à-dire la fréquence à laquelle une paroi simple entre en résonance et a très peu d'effet de réduction sonore) ? j'ai regardé les fiches produits mais n'ai trouvé cela nulle part. Y a t-il une formule pour la calculer a partir de la densité et l'épaisseur du matériau ?
TROISIÈME QUESTION
J'ai un mal de chien à trouver l'indice d'affaiblissement acoustique R (ou Rw j'ai vu parfois) des différents matériaux. Et quand c'est indiqué, je comprends mal ce à quoi cela correspond. Par exemple sur cette fiche, qui concerne le placo phonique Knauf KA13:
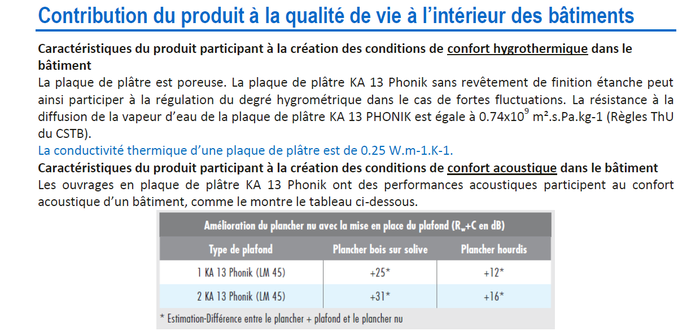
Pourquoi indiquent-il Rw+C (qu'est-ce que ce C ? La vitesse de propagation des ondes sonores ? 340m/s ? et qu'est-ce que ça indique/vient faire ici ?) Et qu'entendent-ils par "amélioration du plancher" ? Et quand ils mettent +35db, c'est 35 dB de réduction du son ? Bref, si quelqu'un veut bien éclairer ma lanterne sur ce qu'il se passe dans cette fiche produit, je suis preneur !
QUATRIÈME QUESTION
Concernant les ondes stationnaires qui apparaissent dans le vide d'air entre les deux parois, j'ai bien vu que l'enjeu est de faire en sorte qu'elles soient les plus aigus possibles. Pour cela la meilleure solution est de réduire le vide d'air, mais cela entre en conflit avec la nécessité d'agrandir ce même vide d'air, qui permet de faire baisser la fréquence de résonance de la cabine. L'astuce est alors de mettre de la laine minérale/un amortisseur qui laisse ce vide d'air tout en stoppant la formation d'ondes stationnaires.
Mais est-il quand même important de laisser un réel vide d'air ? Dans le cours, ils disent que la fréquence des ondes stationnaires doit être le plus aigu[ possible : est-ce que si on bouche entièrement l'espace entre les deux parois avec de la laine, ça ne supprime pas purement et simplement ces ondes ? Dans ce cas pourquoi s'en priver ? est-ce que remplir complètement cet espace de laine nuit aux performances d'atténuation acoustique de l'ensemble?
Voilà, c'est tout pour l'instant, je découvre le domaine !
Je crée ici un post car je me penche sur la physique acoustique pour essayer de construire au mieux une cabine dans laquelle je puisse jouer dans mon appartement. Je suis en train de m'y mettre grâce à ce cours très clair : http://www.ac-grenoble.fr/lycee/roger.deschaux/documents/Cours/Acoustique/Acoustique-Cours_1.pdf
J'essaye d'organiser ce post de manière cohérente.
PREMIÈRE QUESTION
Je joue du saxophone ténor. La note la plus grave (Bb, Ab en ut) semble descendre assez bas dans le spectre des fréquences. Je vous mets ici une illustration.
Il faut donc construire une cabine qui ait une fréquence de résonance qui soit plus basse que celles du saxophone dans sa note la plus grave, donc, en gros il faut que la fréquence de résonance de la cabine soit en dessous de 100Hz.
Je ne peux pas faire de cloison trop épaisses pour la cabine, je suis parti sur 15 cm maximum, avec 10 cm de vide d'air (ou avec laine de roche) maximum.
J'ai appliqué la formule suivante : fr (fréquence de résonance) = 84 √(1/d)*((1/m1) + (1/m2)), d étant le vide d'air (en mètre) et m1 et m2 la masse surfacique des deux parois désolidarisées de la cabine.
Je pars sur deux matériaux différents pour les deux parois, pour éviter qu'ils aient la même fréquence critique. J'ai donc fait des test avec une plaque de BA13 phonique, de masse surfacique de 11.2kg/m² ; et une plaque de BA18, de masse surfacique de 16.8kg/m².
Voici les résultats.
- Avec un vide d'air de 6 cm, la fréquence de résonance de la cabine est de 132Hrz .
- avec un vide d'air de 8 cm, la fréquence de résonance de la cabine est de 114.5Hrz
- avec un vide d'air de 9 cm la fréquence de résonance est de 108Hrz
- avec un vide d'air de 10cm, la fréquence de résonance est de 102Hrz.
J'ai essayé de remplacer le BA18 par du BA25, de masse surfacique de 18.3kg/m²:
- avec un vide d'air de 6 cm, la fréquence de résonance de la cabine est de 130Hrz.
- avec un vide d'air de 8cm, la fréquence de résonance de la cabine est de 112Hrz.
J'ai été choqué par le peu de différence que le changement d'épaisseur du placo produisait sur la fréquence de résonance de l'ensemble de la cabine.
Quoi qu'il en soit, tous ces résultats sont insatisfaisants, et la cabine risque de résonner quand je joue dans les graves, ce qui serait contre-productif, pire encore que de jouer sans cabine.
Quelqu'un connaîtrait-il une équation miracle pour réduire la fréquence de résonance de la cabine(une savant combinaison de deux masses surfaciques spécifiques peut-être ?) ou bien la seule solution est-ce d'accroitre le vide d'air ?
DEUXIÈME QUESTION
Comment peut-on connaître la fréquence critique des différents matériaux (c'est-à-dire la fréquence à laquelle une paroi simple entre en résonance et a très peu d'effet de réduction sonore) ? j'ai regardé les fiches produits mais n'ai trouvé cela nulle part. Y a t-il une formule pour la calculer a partir de la densité et l'épaisseur du matériau ?
TROISIÈME QUESTION
J'ai un mal de chien à trouver l'indice d'affaiblissement acoustique R (ou Rw j'ai vu parfois) des différents matériaux. Et quand c'est indiqué, je comprends mal ce à quoi cela correspond. Par exemple sur cette fiche, qui concerne le placo phonique Knauf KA13:
Pourquoi indiquent-il Rw+C (qu'est-ce que ce C ? La vitesse de propagation des ondes sonores ? 340m/s ? et qu'est-ce que ça indique/vient faire ici ?) Et qu'entendent-ils par "amélioration du plancher" ? Et quand ils mettent +35db, c'est 35 dB de réduction du son ? Bref, si quelqu'un veut bien éclairer ma lanterne sur ce qu'il se passe dans cette fiche produit, je suis preneur !
QUATRIÈME QUESTION
Concernant les ondes stationnaires qui apparaissent dans le vide d'air entre les deux parois, j'ai bien vu que l'enjeu est de faire en sorte qu'elles soient les plus aigus possibles. Pour cela la meilleure solution est de réduire le vide d'air, mais cela entre en conflit avec la nécessité d'agrandir ce même vide d'air, qui permet de faire baisser la fréquence de résonance de la cabine. L'astuce est alors de mettre de la laine minérale/un amortisseur qui laisse ce vide d'air tout en stoppant la formation d'ondes stationnaires.
Mais est-il quand même important de laisser un réel vide d'air ? Dans le cours, ils disent que la fréquence des ondes stationnaires doit être le plus aigu[ possible : est-ce que si on bouche entièrement l'espace entre les deux parois avec de la laine, ça ne supprime pas purement et simplement ces ondes ? Dans ce cas pourquoi s'en priver ? est-ce que remplir complètement cet espace de laine nuit aux performances d'atténuation acoustique de l'ensemble?
Voilà, c'est tout pour l'instant, je découvre le domaine !
Jean-Pierre B.
1365
AFicionado·a
Membre depuis 6 ans
1-En augmentant la distance entre les masses et/ou en augmentant la masse surfacique.
Conseil: mieux vaut deux masses identiques de chaque côté qui créeront une fréquence de résonance plus basse par rapport à deux masses différentes aillant une fréquence de résonance plus haute.
Plus la fréquence de résonance est basse meilleure sera l'isolation....à condition que la fréquence de résonance soit en dessous de la fréquence la plus basse jouée.
Si la fréquence de résonance = note jouée, alors le système amplifie cette fréquence.
On a alors donc une isolation moins bonne qu'avec une seule paroi qui répond à la loi de masse.
2-
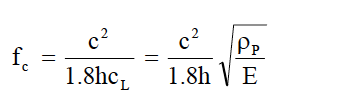
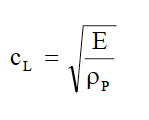
ρP = Densité (en kg/m²)
E : Module d'élasticité (N/m²)
C=343m/s pour T=20°C
3- J'y reviendrai.
4- la fréquence de résonance doit être la plus basse possible comme vous l'avez dit dans la première partie.
La laine entre les deux parois sert à atténuer et baisser cette fréquence.
J'ai designé une isolation pour une cabine, 15cm d épaisseur, fréquence de résonance calculée : 50hz.
L'isolation commence à 70hz (50*√²).
L'instrument de la note la plus basse est 200hz.
On a ici un rapport de 4 (200/50).
Bon courage pour la suite! et content de voir que vous creusez le sujet
Conseil: mieux vaut deux masses identiques de chaque côté qui créeront une fréquence de résonance plus basse par rapport à deux masses différentes aillant une fréquence de résonance plus haute.
Plus la fréquence de résonance est basse meilleure sera l'isolation....à condition que la fréquence de résonance soit en dessous de la fréquence la plus basse jouée.
Si la fréquence de résonance = note jouée, alors le système amplifie cette fréquence.
On a alors donc une isolation moins bonne qu'avec une seule paroi qui répond à la loi de masse.
2-
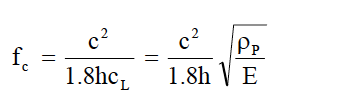
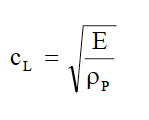
ρP = Densité (en kg/m²)
E : Module d'élasticité (N/m²)
C=343m/s pour T=20°C
3- J'y reviendrai.
4- la fréquence de résonance doit être la plus basse possible comme vous l'avez dit dans la première partie.
La laine entre les deux parois sert à atténuer et baisser cette fréquence.
J'ai designé une isolation pour une cabine, 15cm d épaisseur, fréquence de résonance calculée : 50hz.
L'isolation commence à 70hz (50*√²).
L'instrument de la note la plus basse est 200hz.
On a ici un rapport de 4 (200/50).
Bon courage pour la suite! et content de voir que vous creusez le sujet
Acoustic Designer @ Neutral & Natural Acoustics
Consultation Acoustique -> me contacter par message privé.
[ Dernière édition du message le 15/11/2019 à 10:28:40 ]
Sardino
73
Posteur·euse AFfranchi·e
Membre depuis 6 ans
Merci beaucoup pour ces précisions ! 
Deux points :
PREMIEREMENT
Du coup j'ai commencé à calculer les fréquences critiques des parois simples.
Or IMPOSSIBLE de trouver le module d'élasticité pour les plaques de plâtres. Il y a des listes pour presque tous les matériaux mais pas le placo.
J'ai trouvé du coup une formule légèrement différente :
Au lieu de cL dans la formule de Jean-Pierre, il y a ici c1 : vitesse de propagation du son dans le matériau.
Ils donnent ici c1 pour le plâtre. Mais est-ce qu'une plaque de placo = simplement du plâtre ? Est-ce que je peux me fonder sur ce tableau pour connaître la vitesse de propagation du son dans le placo ?
Si tel est le cas, alors j'ai fait le calcul : une double épaisseur de placo phonique BA13 a une fréquence critique autour de 1000Hrz... Ce qui n'est pas bien du tout non ?
DEUXIEMEMENT
Dans le calcul de la fréquence de résonance du système masse-ressort-masse, la formule utilisée ne semble pas prévoir de place pour calculer l'influence de la laine de roche :
Fréquence de résonance = 84 √(1/d)*((1/m1) + (1/m2)).
d = vide d'air (en mètre)
m1 et m2 : masses surfacique des deux parois. (en kg/m²)
Comment calculer l'influence de la laine de roche pour faire baisser la fréquence de résonance ? Et comment savoir du coup quelle densité et épaisseur de laine de roche placer au sein du vide d'air ?
Deux points : PREMIEREMENT
Du coup j'ai commencé à calculer les fréquences critiques des parois simples.
Or IMPOSSIBLE de trouver le module d'élasticité pour les plaques de plâtres. Il y a des listes pour presque tous les matériaux mais pas le placo.
J'ai trouvé du coup une formule légèrement différente :
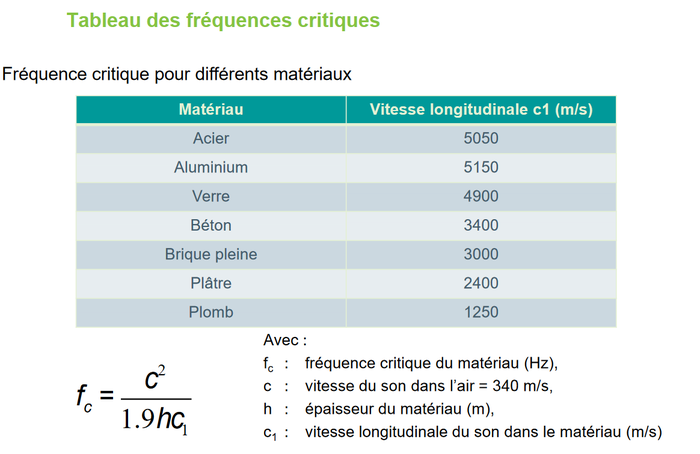
Au lieu de cL dans la formule de Jean-Pierre, il y a ici c1 : vitesse de propagation du son dans le matériau.
Ils donnent ici c1 pour le plâtre. Mais est-ce qu'une plaque de placo = simplement du plâtre ? Est-ce que je peux me fonder sur ce tableau pour connaître la vitesse de propagation du son dans le placo ?
Si tel est le cas, alors j'ai fait le calcul : une double épaisseur de placo phonique BA13 a une fréquence critique autour de 1000Hrz... Ce qui n'est pas bien du tout non ?
DEUXIEMEMENT
Dans le calcul de la fréquence de résonance du système masse-ressort-masse, la formule utilisée ne semble pas prévoir de place pour calculer l'influence de la laine de roche :
Fréquence de résonance = 84 √(1/d)*((1/m1) + (1/m2)).
d = vide d'air (en mètre)
m1 et m2 : masses surfacique des deux parois. (en kg/m²)
Comment calculer l'influence de la laine de roche pour faire baisser la fréquence de résonance ? Et comment savoir du coup quelle densité et épaisseur de laine de roche placer au sein du vide d'air ?
[ Dernière édition du message le 15/11/2019 à 17:10:55 ]
Chris Kazvon
17116
Drogué·e à l’AFéine
Membre depuis 12 ans
intéressant !!
je flague pour lire à tête reposée plus tard
Chris Kazvon
-------------------------------------------------
Introduction à Hornresp et Tutoriels - Tutoriels Vidéo pour Room EQ Wizard
- < Liste des sujets
- Charte