Spectre harmonique de l'onde en dent de scie ?
- 67 réponses
- 14 participants
- 24 102 vues
- 13 followers
francolamuerte
Bonjour à tous !
Le 02 Octobre 2006 je mettais en ligne sur ReasonFrance un de mes tutos sur les harmoniques, que vous pouvez consulter à cette adresse :
:arrow: Les harmoniques
Sur le thread du tuto en question s’est développé quelques questionnements. Une question particulièrement semblant assez triviale sur lequel j’achoppe toujours est :
« Pourquoi l’onde en dent de scie comporte en son spectre toutes les harmoniques » ?
Je suis renseigné à propos du fait que selon le théorème de Fourier n’importe quel type de signal périodique peut se décomposer en une simultanéité de plusieurs ondes sinusoïdales.
Mais si vous pouviez m’aider à comprendre « pourquoi » l’onde en dent de scie génère ce spectre harmonique riche, je vous en serait bien reconnaissant. J’ai décidé de venir scruter le terrain sur Audio Fanzine car je sais que certains membres ici possèdent de solides acquis quant à la nature même du son.
Bien à vous ![]()
Je vous fait le résumé des quelques post qui ont générés cette interrogation sur ReasonFrance :
Citation : [quote="francolamuerte"]mes compétences en synthèse sonore comportent ses limites. Je ne saurais pas exactement ( pour l'instant ;) ) te dire, sur le fond, POURQUOI l'onde en dent de scie génère toute la série des harmoniques, mais tu peux me croire sur la forme... du reste si quelqu'un passe par ici et saurait dire POURQUOI l'onde en dent de scie comporte toutes les harmoniques, soyez généreux !
Aidez Franco s'il vous plait mes amis ![/quote]
Citation : simple convention non?
peut être qu'a l'époque des premiers sythétiseurs on été capable de générer que ce genre de signaux electriques?
Citation : Convention ? Qu'est-ce que tu entends par « convention » Davie ?
Pourquoi l'onde en dent de scie comporte toutes les harmoniques dans son spectre et pourquoi l'onde sinus n'en contient aucune ? Ça peut pas s'expliquer de façon mathématique-scientifique tu crois par rapport à la forme d'onde etc... ? Je pose ce genre de question dans le genre « pourquoi le feu c'est chaud ? » Simple convention ? ![]() Le fait que l'onde en dent de scie comporte toutes les harmoniques en son spectre serait donc une vérité première, un postulat de base qu'on ne peut réduire en multiples facteurs causals ?
Le fait que l'onde en dent de scie comporte toutes les harmoniques en son spectre serait donc une vérité première, un postulat de base qu'on ne peut réduire en multiples facteurs causals ?
Mais merci à toi Davie de venir en aide au pauvre pélerin de la vérité que je suis.
Citation : Je dirais qu'il s'agit en fait du theoreme de fourier ... ce theoreme dit que toute fonction periodique peut s'exprimer sous la forme d'une somme d'ondes sinusoidales ( si je ne me trompe pas ... multiples de la premiere )
Dès lors : La forme d'onde dent de scie peu se decomposer en plusieures ondes sinusoidales representant chacune une harmonique !
Non ?
Citation : Sans doute merci ! Est-ce qu'on peut « voir » les diverses sinus représentant les harmonique sur l'onde en dent de scie physiquement ? Pourtant lorsque l'on regarde le dessin d'une courbe d'onde en dent de scie on ne voit pas trop de sinus. Mais remarque je viens de tomber par harsard sur un site avec théorème de Fourrier et un dessin qui créditerait ce que tu avances Supergeoff. Pour accéder au site avec les formules mathématiques qui me font peur :
CLIQUEZ SUR L'IMAGE !
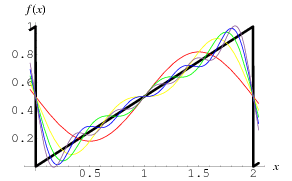
On avance, on avance ! Merci !
Citation : Ouhla ! J'ai qu'un bac S ... je vous aiderais bien plus mais ca ne va pas aussi loin ...
J'ai fait ca l'année derniere en Spé Physique il y avais un chapitre sur la transmission des ondes Radio ... on a debordé parce que la programme etait fini et que le prof ne voulait pas nous laisser rentrer chez nous ...
Si j'avais su que je le ressortirais un jour j'aurais mieux ecouté ! M'enfin c'etait des expliquations très générales ... pas aussi compliquées que ça !
Nous faudrais un Ingé son ? ou bien un physiciens ...
Citation :
Citation : Convention ? Qu'est-ce que tu entends par « convention » Davie ?
j'avoue ne pas saisir quelle question tu te poses précisément... :?
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute ![]() : )
: )
:arrow: Pour quelles raisons, par quels types de liens causals, par quels phénomènes physiques et mathématiques, enfin plus simplement, comment peut-on expliquer le fait que l'onde en dent de scie comporte en son spectre sonore toute la série des harmoniques ? Nous avons déjà une piste ici apportée par Supergeoff, l'onde en dent de scie peut selon le théorème de Fourier se décomposer en plusieurs ondes sinusoïdales, lesquelles correspondent justement à chaque harmonique du spectre sonore.
Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
Pour reprendre mon analogie du feu. Pourquoi le feu c'est chaud ? On pourrait me dire parce qu'il y a un phénomène interne physique qui dégage de l'énergie. Pourtant bien que ça puisse être une réponse louable, ça me laisse sur ma faim. De même lorsque l'on m'indique que l'onde en dent de scie selon le théorème de Fourrier comporte toutes les harmoniques du spectre et que son onde peut se déduire en diverses sinus puisque qu’il s’agit d’un son périodique, et bien je reste encore sur ma faim.
Au fond je crois que j’en suis arrivé à un stade où je devrai impérativement comprendre certains principes mathématiques, certaines lois physiques du son, sinon je ne pourrai pas vraiment comprendre POURQUOI l’onde en dent de scie comporte la série de toutes les harmoniques dans son spectre sonore.
Tu cernes un peu mieux mon incompréhension maintenant Davie ?
Bien à toi ![]()
Citation :
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute Laughing : )
justement je ne crois pas que la réponse de supergoff explique pourquoi l'onde dent de scie contient toutes les harmoniques ;) elle explique juste qu'elle contient toutes les harmoniques
Citation : Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
c'est pas toi qui a fait ue session de synthèse additive sur reason? et qui viens de me dire que l'onde sinus ne contenait aucun harmonique? donc si cest bien ça que tu veux savoir tu l'as ta réponse non :P
Citation : [quote="Davie_Addison"]
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute Laughing : )
justement je ne crois pas que la réponse de supergoff explique pourquoi l'onde dent de scie contient toutes les harmoniques ;) elle explique juste qu'elle contient toutes les harmoniques
Quand je dis que je redoute la réponse, ce n’est pas celle de Supergeoff puisque comme je le disais dans mon précédent message, sa réponse, bien que très louable ne m’avance pas plus dans ma quête de vérité. C’est un peu comme si on me disait :
« Lorsque tu lances une pierre dans les airs, il faudra t’attendre à ce que cette pierre redescende. Une fois lancée, la pierre diminuera de vitesse, elle atteindra un moment inévitable ou elle retombera avec une vitesse toujours croissante jusqu'à ce qu'elle vienne s'écraser par terre. »
Tu comprendras Davie qu’on peut aller plus loin que ça dans le processus de compréhension. C’est je crois ce que je tente de faire avec le phénomène qui nous préoccupe. Quand je dis redouter la réponse à ma question, c’est parce que je sais très bien que ça sera pas de la tarte. Si comme le disait Supergeoff, un physicien traînait dans le coin et commençait à m’expliquer le théorème de Fourier dans le détail et de tout ce qui s’y rattache afin que je puisse bien comprendre pourquoi l’onde en dent de scie comporte en son spectre toute la série des harmoniques, je crois bien que ça serait redoutable pour moi que d’essayer de comprendre, notamment de comprendre toutes les formules mathématiques se rattachant à l’explication.
Cap_PDT_01_13
Citation :
Citation : Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
c'est pas toi qui a fait ue session de synthèse additive sur reason? et qui viens de me dire que l'onde sinus ne contenait aucun harmonique? donc si cest bien ça que tu veux savoir tu l'as ta réponse non :P
Il est vrai que j’ai proposé cette session de Synthèse additive avec Reason, il est vrai qu’on y apprend ceci au tout début :
Citation : La Synthèse sonore additive consiste à créér un son en superposant des signaux sinusoïdaux harmoniques.
Principe
Depuis Joseph Fourier, on sait qu'un signal périodique peut être décomposé en somme de sinus et cosinus, de fréquences multiples de la fréquence fondamentale du signal. Ce sont ces signaux élémentaires qui sont utilisés dans la synthèse additive pour obtenir des sons plus complexes. Cette méthode permet théoriquement de créer tous les sons périodiques.
Je comprends très bien le fait que c’est en juxtaposant plusieurs ondes sinus ( dépourvues d’harmoniques donc ) que l’on vient qu’à créer un son plus riche, plus complexe. Et je sais bien que si on en venait à juxtaposer pleins de sinus correspondant au spectre harmonique total, nous verrions apparaître donc l’onde en dent de scie puisque cette dernière peut se décomposer en plusieurs sinus correspondant aux fréquences du spectre harmonique total.
Cependant tu vois je ne vois là seulement que l’explication de surface. C’est un peu comme si on me disait : « Lance ta pierre dans les airs et elle retombera ensuite par effet de gravité ». Pour vraiment comprendre pourquoi la pierre retombe, cette réponse, en toute bonne foi ne m’est pas du tout satisfaisante.
C’est donc dans le même état d’esprit que je pose la question ici à savoir, je le répète, pourquoi l’onde en dent de scie comporte toutes la série des harmoniques en son spectre ?
Merci pour ton retour Davie et merci à tous ! ![]() [/quote]
[/quote]
Citation :
Citation :
Tu comprendras Davie qu’on peut aller plus loin que ça dans le processus de compréhension. C’est je crois ce que je tente de faire avec le phénomène qui nous préoccupe. Quand je dis redouter la réponse à ma question, c’est parce que je sais très bien que ça sera pas de la tarte. Si comme le disait Supergeoff, un physicien traînait dans le coin et commençait à m’expliquer le théorème de Fourier dans le détail et de tout ce qui s’y rattache afin que je puisse bien comprendre pourquoi l’onde en dent de scie comporte en son spectre toute la série des harmoniques, je crois bien que ça serait redoutable pour moi que d’essayer de comprendre, notamment de comprendre toutes les formules mathématiques se rattachant à l’explication.
le problème c'est qu'il va te falloir prendre quelques cours de maths pour ça ;)
toi qui aimes les images... c'est un peu comme si un type venait te voir en disant "j'ai feuilleté 2 traités d'harmonie, explique moi comment on fait une fuge" (;)) tu vois que le situation est en somme toute un peu cocasse...
dans le sens ou même si quelqu'un t'expliquera concretement ces séries de fourrier avec toute les capture d'écrans retouchées sur paint qu'il aura pu faire, tu ne pourra pas aller aller immédiatement vers la compréhension. Cette compréhension nécessite des acquis d'outils mathématiques usuels...
enfin là encore le théromère de Fourrier n'esxplique pas pourquoi l'onde dent de scie contient toutes les harmoniques... il explique qu'il existe une onde qui contient toutes les harmoniques ![]()
peut être te poses tu la mauvaise question? ou peut être ne t'ais je toujours pas compris ![]()
![]()
![]()
![]()
Citation : L'analyse par le théoreme de fourier est la meilleure piste de compréhension je pense, mais ca n'est pas simple mathématiquement.
Par contre tu peux interpréter ce théoreme de facon "graphique".
L'idée est de se dire qu'un ajoutant différentes formes de sinusoide, tu peux créer une autre forme. Ces différentes sinusoides peuvent etre d'amplitude différentes du signal à atteindre, et de fréquence différentes.
La complexité des équations de fourier exprime le probleme suivant ( je fais de la vulgarisation volontairement)
La sinuisoide est un signal avec des "courbes continues". Une courbe est simple à décrire à partir d'une règle mathématique, autant qu'avec un crayon.
Là où ca se complique, c'est quand le signal à modéliser contient des angles.
L'angle est l'ennemi de la courbe. L'angle en soit est une rupture de courbe.
Quand tu veux modéliser par Fourier un "angle", tu es obligé d'aborder des notions "d'infini".
Dit autrement si tu veux faire un signal avec un angle, en partant de signaux avec des courbes, il te faudra une infinité de signaux "courbes" avant d'atteindre cet angle.
Bien entendu, aucune modélisation n'a cette précision, surtout pas reason.
Dans la pratique, si tu consideres un signal triangulaire :
* basiquement : tu l'approximes avec une sinusoide. Ton triangulaire est courbe. c'est dommage, mais c'est à moindre frais ce qu'on propose de mieux
* tu combines 20 sinusoides. Tu commences à obtenir un signal avec une rupture arrondie (c'est joliement dit hein ? ) en haut et en bas. Par contre entre les pics, le signal commence à approcher proprement celui d'un triangulaire
* tu combines une infinité de sinusoides, .....et ton angle de rupture apparait enfin. Ton PC s'écroule, et une météorite kryptonnique s'écrase sur ton clavier.
Voilà pour l'approche graphique de Fourrier.
Ce qu'il faut bien comprendre, c'est que les signaux combinés peuvent ne pas etre de meme fréquence. Sinon il serait impossible d'obtenir le fameux "angle". Pleins de petites sinusoides additionnées donnent une autre sinusoide. En soit ca ne modifie pas la forme finale de l'onde, ca va juste l'allonger, l'étirer. Basta.
Donc si tu simules un signal en dent de scie avec des sinuisoides, effectivement tu vas te retrouver avec différentes composantes sinusoidales de fréquences variées. Ce que tu constates dans ton spectrometre. Leur nombre est aussi élevé que ta courbe "dent de scie" est parfaite.
Voilà, je ne sais pas si j'ai fait avancer le débat. Ce qui est sur c'est que mes ex profs de maths se retournent désormais dans leur tombe. D'ailleurs je les salue bien bas.
Citation : Merci beaucoup Blumblum, c'est exactement le genre de réponse que je voulais susciter, je n'ai pas tout compris certes, mais j'ai l'intuition cependant d'être sur la bonne piste de compréhension, c’est tout ce qui m’importe. Il est vrai, comme le disait Davie Addison, que ça me prendrait des notions mathématiques avancées afin de mieux comprendre cette question. N’empêche je crois malgré tout qu’il est possible, pour un humble pèlerin comme moi, d’avancer tranquillement sur le chemin de la compréhension.
Même si ta réponse Blumblum ne va pas au fond des choses, malgré tout, elle apporte une bonne piste d’investigation que je vais suivre afin d’y voir plus clair. Mais pour l’instant quelques petites questions surgissent.
[quote="blumblum"]Quand tu veux modéliser par Fourier un "angle", tu es obligé d'aborder des notions "d'infini".
J’aimerais bien, être en mesure de comprendre ce que tu entends par « infini ». Comme tu l’as placé entre guillemet c’est sans doute parce que ce terme cache quelque chose de plus révélateur. Je comprendrais si c’est trop complexe à expliquer, mais je ne m’empêcherai pas de poser la question quand même. :mrgreen:
1- Est-ce que « infini » est ici à prendre au sens de : la courbe n’est pas finie elle donc « infinie » et ce en vertu du fait que l’on brise sa courbure finie ?
2- Et ce terme « d’infini » ne serait-il pas à même de décrire justement le spectre harmonique « infini » que peut comprendre l’onde en dent de scie par exemple ?
Citation : Dit autrement si tu veux faire un signal avec un angle, en partant de signaux avec des courbes, il te faudra une infinité de signaux "courbes" avant d'atteindre cet angle.
Bien entendu, aucune modélisation n'a cette précision, surtout pas reason.
3 – Pourtant sur Reason il y a bien l’onde en dent de scie qui est bien présente.
Suivant ce que tu m’indiques, je peux déjà comprendre que l’onde en dent de scie, parce qu’elle est anguleuse, doit nécessairement comporter dans l’architecture de son spectre sonore une infinité de sinusoïde, or tu m’indiques que Reason n’est pas à même de reproduire cela. Mais pourtant l’onde en dent de scie est bien présente dans le logiciel. Est-ce que cela voudrait dire qu’étant donné l’incapacité du logiciel à reproduire l’infini, les concepteurs ont fait en sorte de limiter volontairement le spectre harmonique de l’onde en dent de scie du Subtractor ? Est-ce donc à dire qu’une véritable onde en dent de scie avec un spectre harmonique « infini » est difficilement conceptualisable pour l’homme ? Est-ce que les synthétiseurs hardware analogiques sont à même de reproduire une onde en dent de scie s’approchant davantage de cette notion d’infini puisque l’onde généré est une courbe continu et non pas une courbe créée à partir d’échantillon comme on le fait pour numériser le son ?
Citation : tu combines une infinité de sinusoides, .....et ton angle de rupture apparait enfin. Ton PC s'écroule, et une météorite kryptonnique s'écrase sur ton clavier.
J’ai justement calculé les 300 premières harmoniques de de la sinusoïde « LA ( 55 hertz ) et je les ai fait joué en même temps dans Cubase. Il est à noter que la plus haute sinusoïde se situe à 16 500 Hertz. Voici tout d’abord mes 300 petites waves Sinusoïdes correspondantes aux 300 premières harmoniques de la fondamentale « LA – 55 hertz ». Le numéro de chaque wave correspond à la hauteur en hertz de chaque harmonique.
http://reasonfrance.free.fr/uploadmodos/franco/allharm1.jpghttp://reasonfrance.free.fr/uploadmodos/franco/allharm2.jpg
J’ai importé ces 300 petites waves dans Cubase, je les ai fait jouer en même temps, voici donc le résultat sonore que j’obtiens :
:arrow: 300 premières harmoniques en même temps
Comme on peut l’entendre le résultat sonore s’apparente bien un peu au timbre de l’onde en dent de scie. Cependant si on regarde le graphique de ce 4 secondes d’onde, on aperçoit un dessin pas très commun.
http://reasonfrance.free.fr/uploadmodos/franco/resultat300harm.jpg
Ça ne ressemble pas vraiment à l’onde en dent de scie que l’on connaît. Sans doute qu’il y a des explications à ça. Toutes mes harmoniques étaient à intensités égales dans Cubase, peut-être que pour la formation d’une onde en dent de scie se forme sur certaine harmonique en particulier et que les harmoniques très aiguës sont moins présente en intensité que les harmoniques du bas du spectre ? D’ailleurs tu me l’indique très bien aussi Blumblum
Citation : Ce qu'il faut bien comprendre, c'est que les signaux combinés peuvent ne pas etre de meme fréquence. Sinon il serait impossible d'obtenir le fameux "angle".
Saurais-tu me dire Blumblum qu’elles intensités doivent avoir chaque harmonique afin de retrouver l’onde en dent de scie ?
Peut-être aussi que 300 harmoniques ce n’est pas assez pour obtenir l’onde en dent de scie. ( je rappelle que mon onde la plus haute en fréquence se situe à 16 500 hertz quand même… ).
Malgré tout, si on observe attentivement la courbe d’onde ci-haut, on peut apercevoir une certaine périodicité rappelant assez bien l’onde en dent de scie. Le dessin se perçoit ou se « devine » par ce qu’on peut soustraire du centre du dessin de la courbe d’onde.
Regardez :
http://reasonfrance.free.fr/uploadmodos/franco/resultat300harmsaw.jpg
Évidemment, je ne répond pas du tout à ma question à savoir pourquoi l’onde en dent de scie comporte toutes les harmoniques en son spectre, mais j’avance à petits pas bien humblement dans ce chemin complexe en petit pèlerin branleur plein de bonne foi.
Merci beaucoup Blumblum ! Je vais attendre avec impatience ton retour éclairé à ce propos.
Merci à tous ![]()
[ot]PS à Davie : Désolé encore pour avoir utilisé des graphiques retouchés dans Paint :mrgreen:[/ot][/quote]
Citation :
Citation : PS à Davie : Désolé encore pour avoir utiliser des graphiques retouchés dans Paint Mr. Green
![]()
![]()
![]()
la notion d'infini est un grand "classique mathématique"
elle est a envisager comme non pas une chose qui peut être quantifiable, ou mesurable mais bel et bien infini.
donc pour résumer : (dans la théorie) une onde dent de scie est la somme "infinie" de toutes les harmoniqes d'une fondamentale, c'est aussi simple que ça ![]()
maintenant en pratique, générer une infinité d'harmonique demande une infinité de ressources (processeur...) et nous sommes limités par nos oreilles (on entends pas les sons au delà de 20khz...
Citation : Évidemment, je ne répond pas du tout à ma question à savoir pourquoi l’onde en dent de scie comporte toutes les harmoniques en son spectre, mais j’avance à petits pas bien humblement dans ce chemin complexe en petit pèlerin branleur plein de bonne foi.
et je crois qu'on s'éloigne encore plus de ta question... mais bon on a du temps a perdre après tout ![]()
Citation : On s'éloigne peut-être de la question certes, mais comme tu disais Davie, pour comprendre un tel truc, il faut inévitablement passer par plein d'autres avant de s'attaquer à une telle question. Ceci-dit, je ne trouve pas notre discussion si éloignée que ça de la question. Et puis il est bien normale de discuter de la chair autour de l'os quand cet os nous semble impénétrable.
Citation : donc pour résumer : (dans la théorie) une onde dent de scie est la somme "infinie" de toutes les harmoniqes d'une fondamentale
Tout à fait ! C’est ce qui me semble ressortir de plus simple et de plus général quant à une définition théorique de la question posée. Bien que c’est une réponse sur laquelle il faut patienter, elle offre néanmoins un certain confort sur lequel on peut dormir tranquille. ![]()
[quote="Davie_Addison"]maintenant en pratique, générer une infinité d'harmonique demande une infinité de ressources (processeur...) et nous sommes limités par nos oreilles (on entends pas les sons au delà de 20khz...:
C’est pour ça que je posais la question à Blumblum à savoir est-ce que l’onde en dent de scie générée dans les synthétiseurs numériques a un spectre harmonique n’ont pas infini puisqu’impossible à calculer mais un spectre « fini », déterminé par l’homme et ce notamment en fonction de notre limite auditive situé autour de 20 000 Hertz ? Et est-ce que l’onde en dent de scie générée par des synthétiseurs analogiques s’approchent davantage de cette notion d’infini théoriquement ?
En tout cas c’est passionnant tout ça !
Cap_PDT_01_28[/quote]
Citation :
Citation : Et est-ce que l’onde en dent de scie générée par des synthétiseurs analogiques s’approchent davantage de cette notion d’infini théoriquement ?
Oui il me semle qu'en creusant cette voie, on peut envisager de toucher un bout de réponse...
Ça serait une question à poster dans le forum thématique synthèse sonore d'AF me semble il ;) non pas que nous soyons de joyeux ignorants par ici, mais j'ai pu croiser des gens dont c'était le métier là bas :P
Dr Pouet
Si l'on applique le même déphasage à chaque harmonique, le résultat ne sera pas un triangle.
Exact... Je pense que ça ne sert pas à grand chose d'essayer de donner une définition textuelle. Il faut donner les équations, et basta.
Comme indiqué dans le 1er message de Franco, l'équation pour la série de Fourrier pour la "dent de scie" est donnée ici :
http://mathworld.wolfram.com/FourierSeriesSawtoothWave.html (point 10)
Plus précisément :
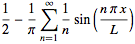
(plus lisible : https://medias.audiofanzine.com/images/thumbs3/1970686.gif - c'est le point 10)
C'est vrai qu'on ne l'a pas du tout pris en compte depuis le début du thread -il me semble-, mais je ne sais pas comment se traduit mathématiquement la phase d'un sinus; Quelqu'un aurait-il la réponse?
La réponse est là : https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Fourier#Coefficients_r.C3.A9els
Voici une harmonique :

Il y a deux façons, équivalentes, de gérer la phase :
- si on adopte la présentation an.cos(nx) + bn.sin(nx), alors la phase est "contenue" dans les coefficients an et bn, et leur rapport entre eux
- si on adopte la présentation Xn.cos(nx + pn) alors pn est la phase pour l'harmonique n
Dans la page wikipedia la ligne suivante donne l'équation pour convertir les coefficients d'une présentation à ceux de l'autre présentation.
Farots
Hors sujet :
Si j'ai donné une définition textuelle, c'est parce que je n'ai pas réussi à intégrer une formule mathématique, ni une image à mes messages. Désolé, et est-ce que quelqu'un pourrait m'aider à ce sujet?
Dr Pouet
Tu as des infos sur la première page :
FAQ : techniques de post (comment mettre des liens, images, smileys, citations, HS, etc)
Sinon tu peux y poser ta (ou tes) questions...
[ Dernière édition du message le 21/04/2011 à 19:13:50 ]
Farots
Hors sujet :
Le lien est buggé
Dr Pouet
corrigé !
Farots
Hors sujet :
Merci Docteur, ça va beucoup mieux maintenant!
C'est peut-être naïf, au niveau maths ou physique, mais je trouve quelquechose de beaucoup plus simple comme formule pour la saw:
Et toujours dans mon optique de "prévoir" une forme d'onde de puis son spectre, est-il prévisible qu'en enlevant le premier harmonique on trouve ça:
En effet, d'après les essais que j'ai effectué sur Grapher, dans

Danguit
d'après les essais que j'ai effectué sur Grapher
Le petit exemple que j'ai montré a été fait avec un script Scilab (très simple). L'un des intérêts est que si l'on choisit bien l'échantillonnage, on peut on peut aussi écouter le résultat (et voir le spectre bien sûr).
Dr Pouet
C'est peut-être naïf, au niveau maths ou physique, mais je trouve quelque chose de beaucoup plus simple comme formule pour la saw.
Beaucoup plus simple ? pas vraiment !
En fait, tu as la même formule,
- avec une petite approximation, car il faut remplacer 1000 par l'infini (mais on s'en doutait)
- pour le reste c'est pareil parce qui compte vraiment c'est le coefficient 1/n ; et seulement sin ou seulement cos (ce qui revient à fixer la phase)
- les autres coefficients doivent assurer un "bon calibrage". Par exemple multiplier x par 2∏/T permet d'avoir une période T ; on peut aussi multiplier x pour 2∏f pour avoir une onde de fréquence f. Mais enfin c'est de la cosmétique.
A partir du moment ou on a une somme de a_b.cos nx + b_n.sin nx, c'est une série de Fourier (ou alors c_n.cos(nx + phase_n) ), et les coefficients a_n et b_n (ou c_n et phase_n) déterminent la phase et les harmoniques.
On peut définir la dent de scie par :
- a_n = 1/n et b_n=0
ou
- c_n= 1/N et phase_n=0
A propos des logiciels, j'ai créé un sujet pour en discuter...
[ Dernière édition du message le 22/04/2011 à 20:52:35 ]
Farots
Citation de Dr Pouet :
...seulement sin ou seulement cos (ce qui revient à fixer la phase)
J'ai peut être mal compris, mais pour cos, je trouve ça:
Danguit
Dr Pouet
On a sin(x)=cos(pi/2 - x) donc à peu près les mêmes fonctions, juste décalées dans le temps.
Du coup, y= Somme (de 1 à ∞, de 1/i*cos(pi/2 - i.x) )
Mais ce ne serait plus une "série de Fourier" car pas exactement mis sous la forme prévue par Fourier (mon message n° 33).
Ton graphique montre que ce problème de phase change complètement la forme de l'onde. Par contre, et sauf nouvelle bêtise de ma part, les harmoniques doivent être à peu près les mêmes ; et donc à l'oreille ça doit sonner de manière similaire ?
Si Danguit peut le vérifier / contredire en audio dans Scilab...
[ Dernière édition du message le 24/04/2011 à 19:07:36 ]
lodeli
Et toujours dans mon optique de "prévoir" une forme d'onde de puis son spectre, est-il prévisible qu'en enlevant le premier harmonique on trouve ça:
previsible... peut etre pas, mais assez clair.
si tu enleves la fondamantale de ta fonction y, ça donne une nouvelle fonction :
y1 = y - sin(x)
c'est à dire le signal en dent de scie de frequence 1/2pi, duquel on deduit une sinusoide de frequence egalement 1/2pi. ce qui correspond bien à ton graphique.
EraTom
Je me permets de ramener mes gros sabots parce qu'après avoir parcouru le sujet en diagonal j'ai lu des trucs qui étaient un peu plus qu'approximatifs (faux, en fait).
Il ne faut pas s'étonner qu'une fonction périodique quelconque ait une infinité d'harmoniques. Dans le cas général c'est toujours le cas et elles tendent vers 0 de façon asymptotique (théorème de Riemann-Lebesgue). Même si les composantes harmoniques sont décroissantes, elles ne sont jamais nulles.
En fait, ce qui est étonnant, c'est plutôt de trouver une fonction qui a un spectre fini. D'ailleurs, à moins de la fabriquer soi-même en sommant quelques sinus et cosinus, ça n'arrive jamais !
D'abord le cadre théorique : (très théorique)
Ça va être long mais pour vraiment répondre à la question... c'est le passage obligatoire.
L'ensemble des fonctions périodiques (de période T) forme un espace Hilbertien.
En clair, c'est un espace vectoriel de dimension infini sur lequel on peut définir un produit scalaire (et un norme).
Pour ceux qui n'ont pas l'habitude de ce genre d'approche c'est peut être très abstrait mais c'est en fait une sorte de géométrie, alors je vais expliquer très grossièrement l'idée.
Un plan forme un espace vectoriel de dimension 2 : un vecteur V peut s'y écrire V = x*i + y*j où (x ; y) sont les coordonnées et le couple i, j sont des vecteurs qui forment une base (et il en faut 2).
Le vecteur V s'écrit comme une combinaison linéaire des vecteurs de base pondérés par les coordonnées.
Il peut y avoir plusieurs bases (en fait, tout couple de vecteurs non colinéaires suffit) et les coordonnées changent si l'on change la base (puisque les coordonnées sont une représentation de V dans une base données).
En 3 dimensions, il faut une coordonnée et un vecteur de base de plus ; un vecteur 3D se décompose en V = x*i + y*j + z*k où ( x ; y ;z ) sont les coordonnées de V dans la base de 3 vecteurs i, j et k
En généralisant le principe, rien n'interdit d'imaginer des espaces de dimensions quelconques... voir avec un nombre infini de dimensions : il suffit d'ajouter des vecteurs de base.
C'est sûr que ce n'est pas facile à imaginer ou à dessiner, mais avec des "formules littérales" ça se fait très bien (en vérifiant quelques propriétés qui garantissent que l'on construit bien un "espace vectoriel" ).
Dans ce cadre, il est possible de montrer que l'ensemble des fonctions périodiques (de période T) forme un tel espace vectoriel et on peut également montrer que l'une des bases possibles est l'ensemble des :
{ 1 ; cos( t*n*2pi/T) ; sin( t*n*2pi/T ) } avec n allant de 1 à l'infini.
Je ne le démontre pas ici, mais ça se fait (en tout cas que je l'ai fait en MathSpé...)
Dit autrement, ça veut dire que n'importe quelle fonction T-périodique s'écrit comme la somme d'une combinaison linéaire des { 1 ; cos( t*n*2pi/T) ; sin( t*n*2pi/T ) } :
f(t) = a0 + ∑ an*cos( t*n*2pi/T ) + ∑ bn*sin( t*n*2pi/T )
Les coefficients ( a0 ; a1 ; ... b1 ; ....) sont les coordonnées du "vecteur" f(t) dans la base { 1 ; cos( t*n*2pi/T) ; sin( t*n*2pi/T ) }
Cette combinaison linéaire, qui n'est "que" la somme des vecteurs de base pondérés par les coordonnées s'appelle la décomposition en série de Fourier (trompettes : tadaaaa).
Il est possible de "décaler" chaque vecteur de base par un déphasage :
{ 1 ; cos( (t+phi) *n*2pi/T) ; sin( (t+phi) *n*2pi/T ) }
On obtient une nouvelle base dans laquelle les coordonnées de f(t) vont changer... Mais f(t) ne change pas : seulement sa décomposition.
Rien n'interdit alors de choisir la base (autrement dit, la phase) qui donnera le jeu de coordonnées le plus simple.
Sauf que je n'ai pas encore dit comment calculer les coordonnées (les coefficients de la série de Fourier).
Pour refaire le parallèle avec le cas 2D, on peut calculer les coordonnées d'un vecteur en le projetant sur les vecteurs de bases.
Comment ? Et bien comme on l'apprend au collège : avec un produit scalaire :
x = V.i
y = V.j
C'est sûr que dans l'espace des fonctions T-périodiques, le produit scalaire est "un peu plus sophistiqué". Dans cette espace, pour deux vecteurs u et v (qui sont des fonctions T-périodique), le produit scalaire se calcule par :
u.v = (2/T) * ∫ u(t)*v(t)*dt pour t allant de -T/2 à +T/2
On peut montrer que cette intégrale définit bien un produit scalaire sur l'espace vectoriel des fonctions T-périodiques.
Pour calculer a0, a1, b1, a2, b2, .... on fait comme dans une espace de dimension 2 : on calcule le produit scalaire du vecteur à décomposer par chaque vecteur de la base. Pour une fonction T-périodique f(t) :
a0 = (2/T) * ∫ f(t) * 1 *dt
a1 = (2/T) * ∫ f(t) * cos( (t+phi) *1*2pi/T) * dt
...
an = (2/T) * ∫ f(t) * cos( (t+phi) *n*2pi/T) * dt
b1 = (2/T) * ∫ f(t) * sin( (t+phi) *1*2pi/T) * dt
...
bn = (2/T) * ∫ f(t) * sin( (t+phi) *n*2pi/T) * dt
Pour répondre à la question :
Si vous avez eu le courage de lire jusqu'ici... chapeau bas.
Donc maintenant, on sait comment la décomposition en série de Fourier est construite et qu'elle est a priori une somme infinie de cos(n*w*t) et sin(n*w*t) (avec w = 2pi/T, appelé la pulsation du fondamental).
Bien sûr, pour certaines fonctions la somme pourra être plus courte, ou plus simple.
Avec un premier exemple, prenons f(t) = cos(t) : sa décomposition va être très simple vu que c'est un des vecteur de base :
a0 = 0, a1 = 1, a2 = 0, ... an = 0 et les bn = 0.
En cas de doute, il suffit de calculer l'intégrale.
Autre exemple, les cosinus sont des fonctions paires et les sinus des fonctions impaires.
On peut alors montrer facilement que si la fonction décomposée est impaire, les coefficients associés aux cosinus seront tous nuls (les an).
Inversement, si la fonction décomposée est paire, alors les coefficients des sinus seront nuls (les bn).
La fonction "dent de scie" admet une symétrie centrale. Il suffit de décaler la base, ou d'introduire un déphasage sur la fonction, pour la transformer en une fonction impaire en plaçant le point de symétrie en t = 0.
On sait donc déjà que tous les an seront nuls dans cette base (pas besoin de les calculer).
Reste à calculer les produits scalaire avec les sin(t*n*w).
Sans perte de généralité, on peut travailler avec la fonction f(t) = t pour t dans
[ Dernière édition du message le 24/04/2011 à 19:42:17 ]
Danguit
Dr Pouet
Et ça ressemble à quoi comme son ?
Danguit
Et ça ressemble à quoi comme son ?
Edit : la nuit portant conseil...
Je me suis aperçu ce matin qu'en fonction de la forme calculée ma carte son arrivait en saturation, ce qui modifiait pas mal le son.
- En reprenant avec un niveau plus correct, je n'arrive plus à différencier sin et cos => mea culpa !
- Au casque avec phase nulle d'un côté, un déphasage constant de l'autre le signal se promène en fonction de la phase.
- Avec déphasage aléatoire (sur chaque harmonique) il y a de subtiles différences de sonorité.
Conclusion, il faut se méfier des conclusions hâtives !
Nota : pour éviter les incompréhensions, j'ai enlevé ce que j'avais répondu précédemment.
Sauvegarder les fichiers son et trouver un hébergeur temporaire pour pouvoir les entendre ici me paraît un peu compliqué (et surtout fastidieux). En revanche, si quelqu'un veut le script pour s'amuser (maquette), pas de problème, c'est de l'ASCII.
[ Dernière édition du message le 25/04/2011 à 08:04:15 ]
EraTom
∑ (1/i) * cos(i*t + (i-1)*π/2)
Si vous utilisez cette formule, vous allez retrouver le signal de départ décalé dans le temps avec les harmoniques aux mêmes endroits dans le spectre et qui présentera la même sonorité.
Voici ici les 2 graphiques avec les 10 premières harmoniques :
L'oreille n'est pas sensible à un décalage de phase "global" mais chaque harmonique est décalée proportionnellement au facteur sur la pulsation :
y(t) = ∑ (1/i) * sin(i*t)
Le signal déphasé y(t+φ) devrait "sonner" exactement de la même manière :
y(t+φ) = ∑ (1/i) * sin(i*(t+φ))
y(t+φ) = ∑ (1/i) * sin(i*t+i*φ)
Pour décaler le signal initial d'une phase de φ, il faut décaler la ième harmonique de i*φ, sinon les harmoniques ne sont pas déphasées correctement.
Si vous remplacez le sinus du fondamental par un cosinus, ça revient à introduire un déphase de φ = π/2. Donc les harmoniques doivent être décalées de i*π/2.
sin(i*t + i*π/2) = sin(i*t + (i-1)*π/2 + π/2 ) = cos(i*t + (i-1)*π/2)
Pour passer à des cosinus il faut donc calculer :
y(t+π/2) = s(t) = ∑ (1/i) * cos(i*t + (i-1)*π/2)
Si les harmoniques ne sont pas décalées selon ce schéma, des artéfacts sonores apparaissent et ils peuvent devenir franchement audibles.
C'est ce qui peut arriver avec certains mauvais EQ dont les filtres n'introduisent pas les mêmes retards dans chaque bande du spectre.
[ Dernière édition du message le 25/04/2011 à 15:34:49 ]
EraTom
Quand on échantillonne un signal à une fréquence de Fe, la plus grande fréquence que l'on peut représenter est de Fe/2.
Toutes celles qui se trouvent au-delà de Fe/2 vont se retrouver sur le bas du spectre et le recouvrir, introduisant de gros artefacts.
C'est aussi vrai en synthèse numérique additive avec la série de Fourier : si le signal synthétisé a une fréquence du fondamental de Fo, avec une fréquence d'échantillonnage de Fe les harmoniques de fréquences i*Fo ne doivent pas dépasser Fe/2.
Il faut donc que i < Fe/(2*Fo) et la somme que constitue la série de Fourier ne doit pas aller au-delà de cette limite, sinon le signal reconstruit ne sera pas celui attendu mais le signal avec aliasing.
Si on veut rajouter des harmoniques il faut bien veiller à ce que Fe soit suffisante.
Dans l'exemple que vous donnez, vous sommez des sin(i*x) pour i allant de 1 à 1000, il faut donc que le pas sur les x soit d'au moins 1/2000 = 5*10^-4.
Un pas plus grand entrainerait du recouvrement spectral ; un pas plus petit augmente le nombre de calculs pour rien.
[ Dernière édition du message le 25/04/2011 à 16:07:20 ]
Farots
Le truc, c'est qu'on était resté dans le théorique, donc pour i = [1; +∞], la question de l'aliasing ne répond pas vraiment au problème (selon moi).
Danguit
Si on veut rajouter des harmoniques il faut bien veiller à ce que Fe soit suffisante.
C'est pour cette raison que sur mon exemple graphique j'ai pris une fondamentale à 100Hz et seulement 100 harmoniques (99 en réalité).
EraTom
Le truc, c'est qu'on était resté dans le théorique, donc pour i = [1; +∞], la question de l'aliasing ne répond pas vraiment au problème (selon moi).
Ce que je disais c'est qu'il n'y a pas 1 problème mais 2 problèmes à surveiller :
- Le premier concerne le "retard de groupe" introduit par le passage au cosinus s'il n'est pas fait correctement.
- Le second concerne la limite du domaine de sommation induit par l'échantillonnage du signal synthétisé.
Concernant l'utilisation des cosinus (tel qu'explicité par Dr Pouet dans son dernier post), l'opération obtenue implique un retard de groupe (les bandes de spectres sont déphasées)
J'ai explicité dans mon post précédent la formule utilisant des cosinus correctement exprimées, sans retard de groupe mais avec un déphasage global qui donne un signal présentant la même sonorité :
y(x) = ∑ (1/i) * cos(i*x + (i-1)*π/2) pour i sur [1; +∞]
Le seul effet sera un retard de l'onde en entier ; le nouvel y(x) aura exactement la même forme et la même sonorité que la version avec des sinus.
L'aliasing c'est effectivement un autre problème mais il intervient dès que tu utilises des moyens de calculs numériques (et a priori sur un ordi c'est le cas).
Il faut faire attention au nombre d'harmoniques utilisé qui est limité par le pas d'échantillonnage.
Sinon, le son synthétisé sera de toute façon fortement "aliasé" et... pour entendre le problème de déphasage de groupe...
Je n'avais pas vu le spectre donné par Danguit. Avec Fe > 100*100*2 = 20kHz ça marche
[ Dernière édition du message le 25/04/2011 à 19:14:25 ]
Dr Pouet
Le truc, c'est qu'on était resté dans le théorique, donc pour i = [1; +∞]
Pareil. Pour obtenir une dent de scie comme sur le dessin.
Mais ce n'est pas inutile de rappeler qu'en numérique il faut couper à Fe/2 (ce que feront tous les logiciels), sinon on aura de l'aliasing, donc des fréquences non souhaitées.
Voici ici les 2 graphiques avec les 10 premières harmoniques :
en utilisant des sinus
en utilisant des cosinus
Super ! Je vois que tu maîtrises bien le Wolfram Alpha, je n'avais pas réussi à tracer ces sommes.
Par contre j'ai corrigé la somme de cosinus où il manquait un "plus" (problème avec les URL d'AF apparemment) et où le i semble le faire passer en complexes, d'où la somme de cosinus selon la formule d'EraTom :
∑ (1/i) * cos(i*t + (i-1)*π/2)
Sinon sans corriger la phase on obtient bien le schéma montré par Danguit.
Et pour écouter : ça donne ça.
Tandis qu'avec des sinus ça fait ça.
Á l'oreille les deux se ressemblent (un peu moins d'aigus avec le cos), mais l'analyse harmonique est assez différente. Autant les coefficients de sin donnent directement les amplitudes des sin, autant c'est moins simple côté cos.
Je remarque qu'en utilisant "play" comme fonction pour pouvoir entendre le résultat, WolframAlpha trace l'analyse harmonique. Pratique !
EDIT: croisement de posts avec le dernier d' EraTom !
[ Dernière édition du message le 25/04/2011 à 20:02:03 ]
Danguit
Je n'avais pas vu le spectre donné par Danguit. Avec Fe > 100*100*2 = 20kHz ça marche
Bien sûr !
Par ailleurs si l'on observe les spectres, on peut constater que le niveau affiché n'est pas correct. La raison est que j'ai commencé par prendre une durée quelconque (2^16 ech) et une fenêtre rectangulaire (pas de fenêtre en fait).
En prenant par exemple une durée multiple de la période du signal (ou une fenêtre correcte), on retrouve bien les bons niveaux en valeur efficace, soit 0.707 si l'amplitude est 1.
Danguit
il faut couper à Fe/2 (ce que feront tous les logiciels),
Si je ne m'abuse, les logiciels ne le font que pour ce qui est mis en entrée ou leurs traitements internes.
C'est un peu hors sujet, mais calculer une expression dans un logiciel permet justement de voir les effets du repliement. Par exemple avec Goldwave, on peut faire rapidement des exemples assez didactiques, du style élever au carré un sinus à F=17k avec Fe=44.1k, ou avec Fe=88.2k puis ré-échantillonage à 44.1k, et comparer.
Dr Pouet
Je me trompe (encore) ?
- < Liste des sujets
- Charte



