Spectre harmonique de l'onde en dent de scie ?
- 67 réponses
- 14 participants
- 24 099 vues
- 13 followers
francolamuerte
Bonjour à tous !
Le 02 Octobre 2006 je mettais en ligne sur ReasonFrance un de mes tutos sur les harmoniques, que vous pouvez consulter à cette adresse :
:arrow: Les harmoniques
Sur le thread du tuto en question s’est développé quelques questionnements. Une question particulièrement semblant assez triviale sur lequel j’achoppe toujours est :
« Pourquoi l’onde en dent de scie comporte en son spectre toutes les harmoniques » ?
Je suis renseigné à propos du fait que selon le théorème de Fourier n’importe quel type de signal périodique peut se décomposer en une simultanéité de plusieurs ondes sinusoïdales.
Mais si vous pouviez m’aider à comprendre « pourquoi » l’onde en dent de scie génère ce spectre harmonique riche, je vous en serait bien reconnaissant. J’ai décidé de venir scruter le terrain sur Audio Fanzine car je sais que certains membres ici possèdent de solides acquis quant à la nature même du son.
Bien à vous ![]()
Je vous fait le résumé des quelques post qui ont générés cette interrogation sur ReasonFrance :
Citation : [quote="francolamuerte"]mes compétences en synthèse sonore comportent ses limites. Je ne saurais pas exactement ( pour l'instant ;) ) te dire, sur le fond, POURQUOI l'onde en dent de scie génère toute la série des harmoniques, mais tu peux me croire sur la forme... du reste si quelqu'un passe par ici et saurait dire POURQUOI l'onde en dent de scie comporte toutes les harmoniques, soyez généreux !
Aidez Franco s'il vous plait mes amis ![/quote]
Citation : simple convention non?
peut être qu'a l'époque des premiers sythétiseurs on été capable de générer que ce genre de signaux electriques?
Citation : Convention ? Qu'est-ce que tu entends par « convention » Davie ?
Pourquoi l'onde en dent de scie comporte toutes les harmoniques dans son spectre et pourquoi l'onde sinus n'en contient aucune ? Ça peut pas s'expliquer de façon mathématique-scientifique tu crois par rapport à la forme d'onde etc... ? Je pose ce genre de question dans le genre « pourquoi le feu c'est chaud ? » Simple convention ? ![]() Le fait que l'onde en dent de scie comporte toutes les harmoniques en son spectre serait donc une vérité première, un postulat de base qu'on ne peut réduire en multiples facteurs causals ?
Le fait que l'onde en dent de scie comporte toutes les harmoniques en son spectre serait donc une vérité première, un postulat de base qu'on ne peut réduire en multiples facteurs causals ?
Mais merci à toi Davie de venir en aide au pauvre pélerin de la vérité que je suis.
Citation : Je dirais qu'il s'agit en fait du theoreme de fourier ... ce theoreme dit que toute fonction periodique peut s'exprimer sous la forme d'une somme d'ondes sinusoidales ( si je ne me trompe pas ... multiples de la premiere )
Dès lors : La forme d'onde dent de scie peu se decomposer en plusieures ondes sinusoidales representant chacune une harmonique !
Non ?
Citation : Sans doute merci ! Est-ce qu'on peut « voir » les diverses sinus représentant les harmonique sur l'onde en dent de scie physiquement ? Pourtant lorsque l'on regarde le dessin d'une courbe d'onde en dent de scie on ne voit pas trop de sinus. Mais remarque je viens de tomber par harsard sur un site avec théorème de Fourrier et un dessin qui créditerait ce que tu avances Supergeoff. Pour accéder au site avec les formules mathématiques qui me font peur :
CLIQUEZ SUR L'IMAGE !
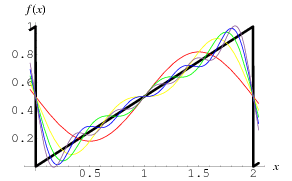
On avance, on avance ! Merci !
Citation : Ouhla ! J'ai qu'un bac S ... je vous aiderais bien plus mais ca ne va pas aussi loin ...
J'ai fait ca l'année derniere en Spé Physique il y avais un chapitre sur la transmission des ondes Radio ... on a debordé parce que la programme etait fini et que le prof ne voulait pas nous laisser rentrer chez nous ...
Si j'avais su que je le ressortirais un jour j'aurais mieux ecouté ! M'enfin c'etait des expliquations très générales ... pas aussi compliquées que ça !
Nous faudrais un Ingé son ? ou bien un physiciens ...
Citation :
Citation : Convention ? Qu'est-ce que tu entends par « convention » Davie ?
j'avoue ne pas saisir quelle question tu te poses précisément... :?
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute ![]() : )
: )
:arrow: Pour quelles raisons, par quels types de liens causals, par quels phénomènes physiques et mathématiques, enfin plus simplement, comment peut-on expliquer le fait que l'onde en dent de scie comporte en son spectre sonore toute la série des harmoniques ? Nous avons déjà une piste ici apportée par Supergeoff, l'onde en dent de scie peut selon le théorème de Fourier se décomposer en plusieurs ondes sinusoïdales, lesquelles correspondent justement à chaque harmonique du spectre sonore.
Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
Pour reprendre mon analogie du feu. Pourquoi le feu c'est chaud ? On pourrait me dire parce qu'il y a un phénomène interne physique qui dégage de l'énergie. Pourtant bien que ça puisse être une réponse louable, ça me laisse sur ma faim. De même lorsque l'on m'indique que l'onde en dent de scie selon le théorème de Fourrier comporte toutes les harmoniques du spectre et que son onde peut se déduire en diverses sinus puisque qu’il s’agit d’un son périodique, et bien je reste encore sur ma faim.
Au fond je crois que j’en suis arrivé à un stade où je devrai impérativement comprendre certains principes mathématiques, certaines lois physiques du son, sinon je ne pourrai pas vraiment comprendre POURQUOI l’onde en dent de scie comporte la série de toutes les harmoniques dans son spectre sonore.
Tu cernes un peu mieux mon incompréhension maintenant Davie ?
Bien à toi ![]()
Citation :
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute Laughing : )
justement je ne crois pas que la réponse de supergoff explique pourquoi l'onde dent de scie contient toutes les harmoniques ;) elle explique juste qu'elle contient toutes les harmoniques
Citation : Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
c'est pas toi qui a fait ue session de synthèse additive sur reason? et qui viens de me dire que l'onde sinus ne contenait aucun harmonique? donc si cest bien ça que tu veux savoir tu l'as ta réponse non :P
Citation : [quote="Davie_Addison"]
Citation : La question est pourtant fort simple ( c'est la réponse que je redoute Laughing : )
justement je ne crois pas que la réponse de supergoff explique pourquoi l'onde dent de scie contient toutes les harmoniques ;) elle explique juste qu'elle contient toutes les harmoniques
Quand je dis que je redoute la réponse, ce n’est pas celle de Supergeoff puisque comme je le disais dans mon précédent message, sa réponse, bien que très louable ne m’avance pas plus dans ma quête de vérité. C’est un peu comme si on me disait :
« Lorsque tu lances une pierre dans les airs, il faudra t’attendre à ce que cette pierre redescende. Une fois lancée, la pierre diminuera de vitesse, elle atteindra un moment inévitable ou elle retombera avec une vitesse toujours croissante jusqu'à ce qu'elle vienne s'écraser par terre. »
Tu comprendras Davie qu’on peut aller plus loin que ça dans le processus de compréhension. C’est je crois ce que je tente de faire avec le phénomène qui nous préoccupe. Quand je dis redouter la réponse à ma question, c’est parce que je sais très bien que ça sera pas de la tarte. Si comme le disait Supergeoff, un physicien traînait dans le coin et commençait à m’expliquer le théorème de Fourier dans le détail et de tout ce qui s’y rattache afin que je puisse bien comprendre pourquoi l’onde en dent de scie comporte en son spectre toute la série des harmoniques, je crois bien que ça serait redoutable pour moi que d’essayer de comprendre, notamment de comprendre toutes les formules mathématiques se rattachant à l’explication.
Cap_PDT_01_13
Citation :
Citation : Mais moi ce que j'aimerais comprendre davantage c'est pourquoi l'onde en dent de scie peut se décomposer en de multiples ondes sinus correspondant aux diverses fréquences du spectre harmonique complet.
c'est pas toi qui a fait ue session de synthèse additive sur reason? et qui viens de me dire que l'onde sinus ne contenait aucun harmonique? donc si cest bien ça que tu veux savoir tu l'as ta réponse non :P
Il est vrai que j’ai proposé cette session de Synthèse additive avec Reason, il est vrai qu’on y apprend ceci au tout début :
Citation : La Synthèse sonore additive consiste à créér un son en superposant des signaux sinusoïdaux harmoniques.
Principe
Depuis Joseph Fourier, on sait qu'un signal périodique peut être décomposé en somme de sinus et cosinus, de fréquences multiples de la fréquence fondamentale du signal. Ce sont ces signaux élémentaires qui sont utilisés dans la synthèse additive pour obtenir des sons plus complexes. Cette méthode permet théoriquement de créer tous les sons périodiques.
Je comprends très bien le fait que c’est en juxtaposant plusieurs ondes sinus ( dépourvues d’harmoniques donc ) que l’on vient qu’à créer un son plus riche, plus complexe. Et je sais bien que si on en venait à juxtaposer pleins de sinus correspondant au spectre harmonique total, nous verrions apparaître donc l’onde en dent de scie puisque cette dernière peut se décomposer en plusieurs sinus correspondant aux fréquences du spectre harmonique total.
Cependant tu vois je ne vois là seulement que l’explication de surface. C’est un peu comme si on me disait : « Lance ta pierre dans les airs et elle retombera ensuite par effet de gravité ». Pour vraiment comprendre pourquoi la pierre retombe, cette réponse, en toute bonne foi ne m’est pas du tout satisfaisante.
C’est donc dans le même état d’esprit que je pose la question ici à savoir, je le répète, pourquoi l’onde en dent de scie comporte toutes la série des harmoniques en son spectre ?
Merci pour ton retour Davie et merci à tous ! ![]() [/quote]
[/quote]
Citation :
Citation :
Tu comprendras Davie qu’on peut aller plus loin que ça dans le processus de compréhension. C’est je crois ce que je tente de faire avec le phénomène qui nous préoccupe. Quand je dis redouter la réponse à ma question, c’est parce que je sais très bien que ça sera pas de la tarte. Si comme le disait Supergeoff, un physicien traînait dans le coin et commençait à m’expliquer le théorème de Fourier dans le détail et de tout ce qui s’y rattache afin que je puisse bien comprendre pourquoi l’onde en dent de scie comporte en son spectre toute la série des harmoniques, je crois bien que ça serait redoutable pour moi que d’essayer de comprendre, notamment de comprendre toutes les formules mathématiques se rattachant à l’explication.
le problème c'est qu'il va te falloir prendre quelques cours de maths pour ça ;)
toi qui aimes les images... c'est un peu comme si un type venait te voir en disant "j'ai feuilleté 2 traités d'harmonie, explique moi comment on fait une fuge" (;)) tu vois que le situation est en somme toute un peu cocasse...
dans le sens ou même si quelqu'un t'expliquera concretement ces séries de fourrier avec toute les capture d'écrans retouchées sur paint qu'il aura pu faire, tu ne pourra pas aller aller immédiatement vers la compréhension. Cette compréhension nécessite des acquis d'outils mathématiques usuels...
enfin là encore le théromère de Fourrier n'esxplique pas pourquoi l'onde dent de scie contient toutes les harmoniques... il explique qu'il existe une onde qui contient toutes les harmoniques ![]()
peut être te poses tu la mauvaise question? ou peut être ne t'ais je toujours pas compris ![]()
![]()
![]()
![]()
Citation : L'analyse par le théoreme de fourier est la meilleure piste de compréhension je pense, mais ca n'est pas simple mathématiquement.
Par contre tu peux interpréter ce théoreme de facon "graphique".
L'idée est de se dire qu'un ajoutant différentes formes de sinusoide, tu peux créer une autre forme. Ces différentes sinusoides peuvent etre d'amplitude différentes du signal à atteindre, et de fréquence différentes.
La complexité des équations de fourier exprime le probleme suivant ( je fais de la vulgarisation volontairement)
La sinuisoide est un signal avec des "courbes continues". Une courbe est simple à décrire à partir d'une règle mathématique, autant qu'avec un crayon.
Là où ca se complique, c'est quand le signal à modéliser contient des angles.
L'angle est l'ennemi de la courbe. L'angle en soit est une rupture de courbe.
Quand tu veux modéliser par Fourier un "angle", tu es obligé d'aborder des notions "d'infini".
Dit autrement si tu veux faire un signal avec un angle, en partant de signaux avec des courbes, il te faudra une infinité de signaux "courbes" avant d'atteindre cet angle.
Bien entendu, aucune modélisation n'a cette précision, surtout pas reason.
Dans la pratique, si tu consideres un signal triangulaire :
* basiquement : tu l'approximes avec une sinusoide. Ton triangulaire est courbe. c'est dommage, mais c'est à moindre frais ce qu'on propose de mieux
* tu combines 20 sinusoides. Tu commences à obtenir un signal avec une rupture arrondie (c'est joliement dit hein ? ) en haut et en bas. Par contre entre les pics, le signal commence à approcher proprement celui d'un triangulaire
* tu combines une infinité de sinusoides, .....et ton angle de rupture apparait enfin. Ton PC s'écroule, et une météorite kryptonnique s'écrase sur ton clavier.
Voilà pour l'approche graphique de Fourrier.
Ce qu'il faut bien comprendre, c'est que les signaux combinés peuvent ne pas etre de meme fréquence. Sinon il serait impossible d'obtenir le fameux "angle". Pleins de petites sinusoides additionnées donnent une autre sinusoide. En soit ca ne modifie pas la forme finale de l'onde, ca va juste l'allonger, l'étirer. Basta.
Donc si tu simules un signal en dent de scie avec des sinuisoides, effectivement tu vas te retrouver avec différentes composantes sinusoidales de fréquences variées. Ce que tu constates dans ton spectrometre. Leur nombre est aussi élevé que ta courbe "dent de scie" est parfaite.
Voilà, je ne sais pas si j'ai fait avancer le débat. Ce qui est sur c'est que mes ex profs de maths se retournent désormais dans leur tombe. D'ailleurs je les salue bien bas.
Citation : Merci beaucoup Blumblum, c'est exactement le genre de réponse que je voulais susciter, je n'ai pas tout compris certes, mais j'ai l'intuition cependant d'être sur la bonne piste de compréhension, c’est tout ce qui m’importe. Il est vrai, comme le disait Davie Addison, que ça me prendrait des notions mathématiques avancées afin de mieux comprendre cette question. N’empêche je crois malgré tout qu’il est possible, pour un humble pèlerin comme moi, d’avancer tranquillement sur le chemin de la compréhension.
Même si ta réponse Blumblum ne va pas au fond des choses, malgré tout, elle apporte une bonne piste d’investigation que je vais suivre afin d’y voir plus clair. Mais pour l’instant quelques petites questions surgissent.
[quote="blumblum"]Quand tu veux modéliser par Fourier un "angle", tu es obligé d'aborder des notions "d'infini".
J’aimerais bien, être en mesure de comprendre ce que tu entends par « infini ». Comme tu l’as placé entre guillemet c’est sans doute parce que ce terme cache quelque chose de plus révélateur. Je comprendrais si c’est trop complexe à expliquer, mais je ne m’empêcherai pas de poser la question quand même. :mrgreen:
1- Est-ce que « infini » est ici à prendre au sens de : la courbe n’est pas finie elle donc « infinie » et ce en vertu du fait que l’on brise sa courbure finie ?
2- Et ce terme « d’infini » ne serait-il pas à même de décrire justement le spectre harmonique « infini » que peut comprendre l’onde en dent de scie par exemple ?
Citation : Dit autrement si tu veux faire un signal avec un angle, en partant de signaux avec des courbes, il te faudra une infinité de signaux "courbes" avant d'atteindre cet angle.
Bien entendu, aucune modélisation n'a cette précision, surtout pas reason.
3 – Pourtant sur Reason il y a bien l’onde en dent de scie qui est bien présente.
Suivant ce que tu m’indiques, je peux déjà comprendre que l’onde en dent de scie, parce qu’elle est anguleuse, doit nécessairement comporter dans l’architecture de son spectre sonore une infinité de sinusoïde, or tu m’indiques que Reason n’est pas à même de reproduire cela. Mais pourtant l’onde en dent de scie est bien présente dans le logiciel. Est-ce que cela voudrait dire qu’étant donné l’incapacité du logiciel à reproduire l’infini, les concepteurs ont fait en sorte de limiter volontairement le spectre harmonique de l’onde en dent de scie du Subtractor ? Est-ce donc à dire qu’une véritable onde en dent de scie avec un spectre harmonique « infini » est difficilement conceptualisable pour l’homme ? Est-ce que les synthétiseurs hardware analogiques sont à même de reproduire une onde en dent de scie s’approchant davantage de cette notion d’infini puisque l’onde généré est une courbe continu et non pas une courbe créée à partir d’échantillon comme on le fait pour numériser le son ?
Citation : tu combines une infinité de sinusoides, .....et ton angle de rupture apparait enfin. Ton PC s'écroule, et une météorite kryptonnique s'écrase sur ton clavier.
J’ai justement calculé les 300 premières harmoniques de de la sinusoïde « LA ( 55 hertz ) et je les ai fait joué en même temps dans Cubase. Il est à noter que la plus haute sinusoïde se situe à 16 500 Hertz. Voici tout d’abord mes 300 petites waves Sinusoïdes correspondantes aux 300 premières harmoniques de la fondamentale « LA – 55 hertz ». Le numéro de chaque wave correspond à la hauteur en hertz de chaque harmonique.
http://reasonfrance.free.fr/uploadmodos/franco/allharm1.jpghttp://reasonfrance.free.fr/uploadmodos/franco/allharm2.jpg
J’ai importé ces 300 petites waves dans Cubase, je les ai fait jouer en même temps, voici donc le résultat sonore que j’obtiens :
:arrow: 300 premières harmoniques en même temps
Comme on peut l’entendre le résultat sonore s’apparente bien un peu au timbre de l’onde en dent de scie. Cependant si on regarde le graphique de ce 4 secondes d’onde, on aperçoit un dessin pas très commun.
http://reasonfrance.free.fr/uploadmodos/franco/resultat300harm.jpg
Ça ne ressemble pas vraiment à l’onde en dent de scie que l’on connaît. Sans doute qu’il y a des explications à ça. Toutes mes harmoniques étaient à intensités égales dans Cubase, peut-être que pour la formation d’une onde en dent de scie se forme sur certaine harmonique en particulier et que les harmoniques très aiguës sont moins présente en intensité que les harmoniques du bas du spectre ? D’ailleurs tu me l’indique très bien aussi Blumblum
Citation : Ce qu'il faut bien comprendre, c'est que les signaux combinés peuvent ne pas etre de meme fréquence. Sinon il serait impossible d'obtenir le fameux "angle".
Saurais-tu me dire Blumblum qu’elles intensités doivent avoir chaque harmonique afin de retrouver l’onde en dent de scie ?
Peut-être aussi que 300 harmoniques ce n’est pas assez pour obtenir l’onde en dent de scie. ( je rappelle que mon onde la plus haute en fréquence se situe à 16 500 hertz quand même… ).
Malgré tout, si on observe attentivement la courbe d’onde ci-haut, on peut apercevoir une certaine périodicité rappelant assez bien l’onde en dent de scie. Le dessin se perçoit ou se « devine » par ce qu’on peut soustraire du centre du dessin de la courbe d’onde.
Regardez :
http://reasonfrance.free.fr/uploadmodos/franco/resultat300harmsaw.jpg
Évidemment, je ne répond pas du tout à ma question à savoir pourquoi l’onde en dent de scie comporte toutes les harmoniques en son spectre, mais j’avance à petits pas bien humblement dans ce chemin complexe en petit pèlerin branleur plein de bonne foi.
Merci beaucoup Blumblum ! Je vais attendre avec impatience ton retour éclairé à ce propos.
Merci à tous ![]()
[ot]PS à Davie : Désolé encore pour avoir utilisé des graphiques retouchés dans Paint :mrgreen:[/ot][/quote]
Citation :
Citation : PS à Davie : Désolé encore pour avoir utiliser des graphiques retouchés dans Paint Mr. Green
![]()
![]()
![]()
la notion d'infini est un grand "classique mathématique"
elle est a envisager comme non pas une chose qui peut être quantifiable, ou mesurable mais bel et bien infini.
donc pour résumer : (dans la théorie) une onde dent de scie est la somme "infinie" de toutes les harmoniqes d'une fondamentale, c'est aussi simple que ça ![]()
maintenant en pratique, générer une infinité d'harmonique demande une infinité de ressources (processeur...) et nous sommes limités par nos oreilles (on entends pas les sons au delà de 20khz...
Citation : Évidemment, je ne répond pas du tout à ma question à savoir pourquoi l’onde en dent de scie comporte toutes les harmoniques en son spectre, mais j’avance à petits pas bien humblement dans ce chemin complexe en petit pèlerin branleur plein de bonne foi.
et je crois qu'on s'éloigne encore plus de ta question... mais bon on a du temps a perdre après tout ![]()
Citation : On s'éloigne peut-être de la question certes, mais comme tu disais Davie, pour comprendre un tel truc, il faut inévitablement passer par plein d'autres avant de s'attaquer à une telle question. Ceci-dit, je ne trouve pas notre discussion si éloignée que ça de la question. Et puis il est bien normale de discuter de la chair autour de l'os quand cet os nous semble impénétrable.
Citation : donc pour résumer : (dans la théorie) une onde dent de scie est la somme "infinie" de toutes les harmoniqes d'une fondamentale
Tout à fait ! C’est ce qui me semble ressortir de plus simple et de plus général quant à une définition théorique de la question posée. Bien que c’est une réponse sur laquelle il faut patienter, elle offre néanmoins un certain confort sur lequel on peut dormir tranquille. ![]()
[quote="Davie_Addison"]maintenant en pratique, générer une infinité d'harmonique demande une infinité de ressources (processeur...) et nous sommes limités par nos oreilles (on entends pas les sons au delà de 20khz...:
C’est pour ça que je posais la question à Blumblum à savoir est-ce que l’onde en dent de scie générée dans les synthétiseurs numériques a un spectre harmonique n’ont pas infini puisqu’impossible à calculer mais un spectre « fini », déterminé par l’homme et ce notamment en fonction de notre limite auditive situé autour de 20 000 Hertz ? Et est-ce que l’onde en dent de scie générée par des synthétiseurs analogiques s’approchent davantage de cette notion d’infini théoriquement ?
En tout cas c’est passionnant tout ça !
Cap_PDT_01_28[/quote]
Citation :
Citation : Et est-ce que l’onde en dent de scie générée par des synthétiseurs analogiques s’approchent davantage de cette notion d’infini théoriquement ?
Oui il me semle qu'en creusant cette voie, on peut envisager de toucher un bout de réponse...
Ça serait une question à poster dans le forum thématique synthèse sonore d'AF me semble il ;) non pas que nous soyons de joyeux ignorants par ici, mais j'ai pu croiser des gens dont c'était le métier là bas :P
Alosely
En fait la réponse à ta question viens effectivement du théorème de fourier qui dit que "toutes fonctions périodiques se décompose en une somme de fonction sinusoïdales, de fréquences multiples de la fréquence fondamentale".
Il y a tout un formalisme mathématique pour démontrer ça, je m'y risquerais pas à faire la démonstration ici ;) (ceci dit, il doit y avoir des tas de sites où tu pourra trouver la démonstration. Mais bon, c'est des maths, et pas forcément faciles...
Mais en gros le résultat, pour une fonction périodique de fréquence F, le théorème de fourier nous dit que cette fonction (qu'on appellera f(t)) peut s'écrire :
f(t) = A0.sin(Ft)+A1.sin(2Ft)+....+An.sin(nFt)+....
la série étant infinie.
maintenant se qui va différencier une fonction périodique d'une autre s'est la valeur des coefficients A0, A1, A2 ... An...
pour une sinusoïde simple ( f(t) = sin(ft) ), on a A0 = 1, et tous les autres coefficients =0. Ce son est très pauvre en harmonique (il n'en a pas en fait)
pour un signal carré, les coefficients An avec n un nombre paire valent tous zéro. Il est plus riche en harmoniques que la fonctions sinus (qui n'a qu'un seul coefficient non nul), mais il manque encore pas mal d'harmoniques.
Pour la dents de scie on retrouve tous les coefficients An sont non nuls. Ce signal contient toutes les harmoniques. Par contre, tous les An n'ont pas la même valeur. Autrement dit plus n est grand plus An est petit.
Si tu prend tous les coefficients An égaux, tu trouvera une autre fonction périodique, qui est le peigne de dirac.
Les synthétiseurs (soustractifs) synthétisent directement l'onde en dents de scie. c'est assez facile à faire de façon analogique et numérique. Le spectre est effectivement infini, mais ça ne pose pas de problème dans se sens là (mais ça en pose effectivement en synthése additive dans la mesure ou l'on doit synthétiser une infinité de fonctions sinusoïdales pour approcher l'onde en dents de scie, ce qui nécessite effectivement des ressources infinies ;) ).
Voilà, je sais pas si j'ai pu apporter un élément de réponse à tes intérogations. Ah oui, à noter que le formalisme de fourier à été développé à la base non pas pour analyser le son (même si aujourd'hui se doit être son application principale), mais ... pour étudier la propagation de la chaleur dans des patates ! Comme quoi, les principes qui se cachent derrière ces concepts mathématiques sont assez généraux et universels...
A+,
V.A.
Choc
Citation : C’est pour ça que je posais la question à Blumblum à savoir est-ce que l’onde en dent de scie générée dans les synthétiseurs numériques a un spectre harmonique n’ont pas infini puisqu’impossible à calculer mais un spectre « fini », déterminé par l’homme et ce notamment en fonction de notre limite auditive situé autour de 20 000 Hertz ? Et est-ce que l’onde en dent de scie générée par des synthétiseurs analogiques s’approchent davantage de cette notion d’infini théoriquement ?
Bah en fait
Fourier te donne la decomposition harmonique d'un signal en dent de scie
Il y a une infinité d'harmoniques

Citation : puisqu’impossible à calculer
C'est pas vraiement ca le probleme. Le probleme c'est qu'en numerique, si ton son possede des frequences qui depassent la moitié de la frequence d'echantillonnage, tu as de l'aliasing. chose a abosluement eviter
resultat, en numerique, on va essayer de synthtiser une dent de scie tout en respectant le fait que l'harmonique max de ta dent de scie soit inferieure a la frequence d'echantillonnage sur deux de ton systeme audio
Site personnel: https://www.enib.fr/~choqueuse/
Choc
Citation : Mais si vous pouviez m’aider à comprendre « pourquoi » l’onde en dent de scie génère ce spectre harmonique riche,
La decomposition en serie de fourier, est une decomposition sur une base de sinusoide
Le fait que la dent de scie comporte une infinité d'harmonique, s'explique simplement par la fait qu'il faut une infinité de sinusoide pour arriver a obtenir un signal dent de scie.
Apres on pourrait se poser la question pourquoi ? intuitivement je dirais que l'angle de la dent de scie, va induire des termes tres hautes frequences, etc...
Site personnel: https://www.enib.fr/~choqueuse/
sygwel
l'angle de la dent de scie nécessite bcp de sinusoides pour être reproduit en raison de son éloigement géométrique (angle vs courbe). voir le schéma plus haut avec la superposition des sinus sur la dent de scie.
et j'ajouterai que plus on rajoute de sinusoides pour reconstruire le signal, plus on se rapprochera de la vraie dent de scie.
mathématiquement, il faudra une infinité de sinusoides pour avoir une dent de scie parfaite.
l'infinité n'étant pas exploitable en pratique, un logiciel par exemple utilisera toujours un nombre fini d'harmoniques sinusoidales pour reconstruire un signal carré.
on en revient à la distinction analogique/numérique : en numérique ou en simulation, où s'arrêter en précision pour construire un signal représentatif du signal analogique, tout en conservant un temps de calcul acceptable.
concept idem que le mp3 : quelles fréquences virer pour optimiser le débit tout en gardant un signal acceptable ? c'est un compromis coût/qualité.
Alosely
Citation : on en revient à la distinction analogique/numérique : en numérique ou en simulation, où s'arrêter en précision pour construire un signal représentatif du signal analogique, tout en conservant un temps de calcul acceptable.
sauf qu'en numérique on n'est pas non plus obligé de synthétiser une dent de scie en ajoutant une par une les harmoniques... il est très facile d'écrire la fonction décrivant la dent de scie (fonction périodique, linéaire sur la période).
Après il est vrai que, du fait qu'en numérique le signal doit être discret (c'est la numérisation), le signal ne sera pas une dent de scie parfaite, mais plutôt une fonction escalier... mais on aura beau faire le calcul en additionnant toute les harmoniques du signal, on résoudra pas ce problème qui est inhérent à la numérisation (d'ailleur synthétiser numériquement une sinusoïde à plus de 20.5kHz lorsqu'on a une fréquence d'échantillonage de 41kHz n'a aucun sens)
francolamuerte
Sans vraiment comprendre tous les détails des calculs mathématiques de Fourier, je crois bien être en mesure d’expliquer la constitution d’une onde en dent de scie.
Je comprends bien qu’il faut absolument avoir une « infinité » d’ondes sinusoïdes pour reproduire à la perfection la carrure de l’onde en dent de scie. Si ce n'est pas une « infinité » ça sera un très grand nombre, comme l'évoque Choc à propos de la numérisation du signal ( aliasing et cie )
Mais pour l'instant prenons une pause, j’ai trouvé une petite animation en flash vraiment bien tripante où l’on peut comprendre « à l’œil » comment se forment différents types d’ondes :
Synthèse Fourier-Animation Flash
Ceci dit, malgré tout ça, je ne sens pas que j’ai réponse à ma question. Je suis conscient aussi que je pose peut-être une question erronée. Mais j’aime bien scruter ce genre de question moins pragmatique avant de me lancer dans l’étude de tous ces calculs mathématiques qui je vous l’avoue me font peur un tantinet.
À date ici et sur le thread en question sur ReasonFrance, j’ai l’impression qu’on me donne des outils pour comprendre « COMMENT » l’onde en dent de scie est constituée sans pour autant indiquer « POURQUOI » l’onde en dent de scie est constitué comme tel. Je sais, la nuance est peut-être pas très indiqué. Je présume lorsque l’on a l’esprit scientifique comme vous trois, on trouve ce genre de question pas très à propos. Du reste vous avez sans doute raison de me dire qu’avec mon « POURQUOI », je ne pose pas la bonne question. Mais pourtant je me la pose. Étant donné que cette discussion a lieu à deux endroits je vous donne ici un de mes messages qui vous donnera un peu plus le ton de mon interrogation qui sans doute n’a pas grand intérêt. Ceci dit, à un niveau plus pratique, je vous remercie, vos réponses m'ont bien éclairé sur certains points !
Merci à tous !
------------------------------------------------------------------------------------------------------------
Citation : la question que franco se posait n'avait rien a voir avec une explication scientifique, je me demande même si finalement elle a une réponse...
Exactement, ce que je suis en train de réaliser je crois !
Citation : Pourquoi l'onde sawtooth contiens toutes les harmoniques?
réponse : d'après le théoréme de Fourrier une onde sawtooth est la somme infinie de toutes les harmoniques d'une fréquence fondamentale donnée
vous avourez que cette réponse ne réponds pas a la question et se contente de décrire le caractère d'une saw....
Voilà Davie tu me comprends ! :idea: En fait ma question transcende ce qu'EST l'onde en dent de scie et s'oriente sur le « POURQUOI » de son existence. Je vous avoue cependant que ce n’est pas une question facile à répondre et comme le dit Davie, peut-être n’y a-t-il pas de réponse. Alors s’il n’y a pas de réponse à « pourquoi l’onde en dent de scie est constituée comme elle est » c’est donc à dire que c’est un postulat de base ? Mais pourtant Blumblum nous affirme ( et avec raison sans doute sur cette question ) qu’il n’existe quasiment pas de postulat de base en mathématique.
En fait les amis pour me comprendre, essayez de vous imaginer que « Comment » et « Pourquoi » sont deux termes bien différents. Le théorème de Fourier, pour ce que j’en connais semble bien nous indiquer « Comment » l’onde en dent de scie est générée, mais ne dit pas pour autant le « Pourquoi » de son existence.
Mais vous savez, même si c’est une question douteuse, voire même si ce n’est pas une bonne question, j’ai souvent besoin d’aller au fond d’un tel raisonnement avant de m’assagir et de commencer à étudier le problème plus en profondeur. Qu’il n’y puisse pas vraiment avoir de réponse à « Pourquoi », au moins je m’y aurai trempé, et c’est avec une quiétude plus accrue que je pourrai me pencher sur le « Comment ».
Citation : J'avoue que je ne comprends pas ce qu'il te manque comme information. Pour etre capable de dessiner un signal dent de scie a partir de sinusoides, il te faut une suite infinie de sinuisoide de fréquence multiples de la fréquence du signal à générer.
Sois sans crainte Blumblum, je sais que ce n’est pas l’information qui me manque si je veux éventuellement recréer une onde en dent de scie à partir de multiples sinusoïdes constituant le spectre harmonique de cette dernière. ( D’ailleurs si vous avez une idée de comment avec au moins 300 harmoniques, la plus haute à 16 500 Hertz, on peut s’approcher de l’onde en dent de scie ça serait sympa de me le faire savoir au passage. J’ai compris que toutes les harmoniques n’avaient pas la même intensité et ce fut mon erreur dans ma petite expérimentation de scientifique branleur plus haut, où j’avais fait jouer à intensité égale toutes mes 300 harmoniques sinusoïdes. )
Je sais qu’on pourrait aussi répondre au « pourquoi » en disant :
-Parce que sinon la synthèse soustractive n’aurait pas existé étant donné qu’elle fonctionne selon un système de filtrage d’une onde riche en harmonique.
Mais encore ici, je sais pas pour vous, mais ça me parait être une réponse plus ou moins satisfaisante. Rien ne justifie l’existence de la synthèse soustractive. Comme je pose le problème, la synthèse soustractive devient un drôle de « postulat à posteriori » pour justifier le fait que l’onde en dent de scie comporte toutes les harmoniques.
HAHA ! Ce beau manège qui tourne en rond dans ma tête.
Citation : moi je serrais d'avis que par simplification scientifique on aie decidé de representer l'onde avec toutes les harmonique par une dent de scie
Il y a quelque chose d’intéressant dans cette réponse Supergeoff. Peut-être l’onde en dent de scie a toujours existé à l’état théorique ( un peu comme les choses existent à priori dans le monde des idées de Platon ). Un scientifique a branché je ne sais quel bidule et ça a donné un son riche et laid ( c’est laid une Saw Tooth pure pas filtrée :mrgreen: ) Ensuite on a expliqué son fonctionnement par le théorème de Fourier ( ce qui je rappelle semble ne pas répondre au « pourquoi » de son existence ) et comme tu dis Supergeoff on lui a attribué le dessin de la dent de scie parce que ça représentait bien ce que le théorème de Fourier semblait indiquer.
Je vous avoue, c’est un peu « psycho » mon truc là. Mais inquiétez-vous pas. Ça va durer un temps chez moi et ensuite vous me verrez le nez dans des livres de Fourier à tenter de comprendre à fond simplement « COMMENT » l’onde en dent de scie peut être constituée.
Bien à vous et merci à vous, c’est super !
PS : Du reste rien n’empêche que l’on peut très bien parler du théorème de Fourier aussi ici. Ça sera sans doute une discussion plus constructive que mes élucubrations périodico-existentielles. HAHA !
sygwel
Citation : on lui a attribué le dessin de la dent de scie parce que ça représentait bien ce que le théorème de Fourier semblait indiquer
non, c'est l'inverse : on part d'une onde observable et on cherche à la modéliser.
le sinus, comme la dent de scie, peut tout à fait exister dans la nature.
Fourrier n'est qu'un outil permettant d'approximer tous les signaux uniquement à partir de sinus, ce qui nous arrange puisqu'un sinus est facile à générer et à manipuler.
les mathématiques (Fourrier) n'ont d'intérêt que pour théoriser la physique (les ondes)
francolamuerte
Donc sujet clo ? On ne peut vraiment pas dire « Pourquoi » l'onde en dent de scie est constituée de la série de toutes les harmoniques ?
C'est une question vicieuse d'après vous ? Ça mène nul part ? C'est pas pertinent ? Ou peut-être la question est mal posée ou n'a tout simplement pas lieu d'être ?
Bien à vous
francolamuerte
Citation : n'oublions pas qu'a l'origine un synthétiseur est sensé émuler les instruments constituants un orchestre, ça aussi ça peut être une piste :P
Davie ( Dead Hollywood Stars pour les Afiens ), tu offres ici sans doute une piste d’investigation qui se rapproche de mon interrogation première du « pourquoi » et non du « comment. » Voyons en quoi cette idée peut être porteuse d’une certaine « vérité ».
Qu’est-ce qui distingue essentiellement la couleur des différents instruments concernant leur timbre ? Si on place plusieurs instruments à la même hauteur sur un La 440 par exemple, qu’est-ce qui nous fera distinguer un instrument par rapport à un autre ? Hors mis l’attaque du son qui est très importante et le type d’enveloppe d’amplitude, nous retrouvons le spectre harmonique de chacun ! Ce spectre sera très différent d’un instrument à l’autre.
Quelle est donc l’onde qui génère le plus d’harmonique en ce monde ? L’onde en dent de scie. C’est donc ensuite par un système de filtre pour atténuer ou faire ressortir certaines zones harmoniques qu’on a pu penser que l’on pouvait ainsi théoriquement reproduire les spectres harmoniques de bons nombres d’instruments existants. Enfin, je présume ? Ça me parait être une piste d’investigation intéressante. Surtout pour le petit branleur mathématicien que je suis qui s’effraie à la vue des diverses formules en arbre de Noël qui, pour moi, n’ont pas l’air d'un cadeau. ( du moins pour l'instant ;) )
Maintenant il serait intéressant de savoir si on a simplement découvert l’onde en dent de scie dans la « nature » ou si c’est une volonté de l’homme. A-t-on dit : « il serait bien de créer une onde avec théoriquement des harmoniques infinies afin d’aller ensuite par un système de filtrage et résonance sculpter par soustraction harmonique le son afin de reproduire les différents spectres harmoniques des instruments acoustiques connus ». ?
Ce genre de réflexion nous propulse dans une zone de « POURQUOI » plutôt que de « COMMENT ». C’est entre autre initialement ce sur quoi je me penchais. Du reste le « comment » est oh combien intéressant ! Seulement avant que je puisse me lancer concrètement dans la compréhension de Fourier et cie, je devrai retourner à l’école ou encore y aller à petite cuillère afin de maîtriser certaines notions de base en mathématique.
Du reste j’ai une autre interrogation qui surgit et je me sens capable d’en appréhender la réponse.
Vous avez vu plus haut mon expérimentation avec les 300 premiers harmoniques de la fondamentale « LA 55 hertz ». Je les ai fait jouer en même temps dans Cubase pensant obtenir une belle onde en dent de scie. Vous avez entendu l’onde et vu le résultat sur graphique. C’est franchement laid et on est très loin de la couleur d’une onde en dent de scie dont la fondamentale serait à 55 hertz. Mon erreur je le répète a été de faire jouer ces 300 harmoniques à la même intensité sonore. Cette notion m’a échappé.
Maintenant je vous demande mes amis, si vous avez un genre de canevas, un genre de graphique, ou un principe qui pourrait me permettre de faire jouer ces 300 harmoniques à des intensités relatives qui me permettrait de faire entendre la couleur d’une onde en dent de scie et de constater sur un diagramme de courbe d’onde une vraie courbure de Saw Tooth et non pas un dessin impropre à ce genre d’onde comme j’ai pu obtenir dans mon expérience amateure.
Si l’onde en dent de scie est produite simplement par l’adjonction d’une série de Sinus basée sur les multiples entiers d’une fondamentale donnée, je pourrais obtenir, même avec seulement 300 harmoniques ( dont la plus haute se situe à 16 500 hertz ), un résultat probant si je savais comment doser les diverses intensités sonores relatives à chacune d’elle. Or je vous demande. Qu’elle est donc cette loi ?
Bien à vous
c d r
Je peu te dire 2 choses :
1- Il ne faut pas prendre le raisonnement dans le sens "Pourquoi une onde en dents de scie génère - elle tels types d'harmoniques?" , car l'onde en dent de scie ne génère rien du tout. C'est le fait que tels types d'harmoniques se produisent qui fait exister une onde en dent de scie (qui n'est qu'une résultante , pas un générateur).
2- La particularité de ces harmoniques est que leur amplitude est assez linéairement décroissant en fonction de leur ordre.(soit fordre1 = fonda , on a fo2 = 2f1 (octave) , fo3 = 3f1 , f04 = 4f1 etc...me semble-t-il...)
franky44
je veux generer une fonction dent de scie sous matlab avec les parametres suivants :
temps de generation
periode
tension min et max
delai de concretisation
si kelk1 peut m'aider svp
plutonak
je suis tombé sur ce thread ce week-end et il m'a inspiré quelques considérations. Je réponds ici avec mon seul niveau de compréhension des choses.
Prenons l’exemple des objets qui tombent. On a donc tous 10 ans et on demande à quelqu’un qui sait, pourquoi la pomme tombe de l’arbre. Newton répondra ; à cause de la gravité, ce champs de forces caractérisé par l’attraction entre deux masses (la terre et la pomme ou la terre et la lune). Certains seront satisfaits, d’autres non, comme Franco. Franco demandera donc : « pourquoi y a-t-il de la gravité ? » ou même « comment explique-t-on l’existence de la gravité ?» (on remarque là, le début de la difficulté à distinguer le pourquoi du comment). Newton ne saura répondre, sa théorie s’arrêtant là. Par contre Einstein dira : « la gravité provient de la courbure de l’espace temps dans lequel les corps massiques suivent certaines trajectoires (des géodésiques), trajectoires qui s’apparentent à l’effet de ce qu’on appelle la gravité même si la gravité n’existe plus vraiment en temps que tel.» Certains seront satisfaits de cette réponse, d’autre non, comme Franco. Franco dira : « pourquoi l’espace temps est-il courbé par les objets massiques? ». Là s’arrête le raisonnement scientifique. Tous les résultats d’Einstein proviennent en gros d’un postulat (phénomène qui est pour l’instant inexpliqué, seulement constaté et auquel on ne peut répondre à la question pourquoi mais qui permet de mettre au point tout un raisonnement en cohérence avec l’expérience) : la lumière se propage à la même vitesse quelque soit le référentiel d’étude.
Revenons maintenant aux ondes sonores. Quand les mathématiciens/physiciens se sont penchés sur le problème du son, ils ont modélisé les entités nécessaires à « leur » compréhension des choses, à savoir la propagation d’une onde dans un milieu continu. Ici, il s’agit donc du son se propageant dans l’air. Peut-être qu’ils se trompent complètement (il est bien connu qu’une théorie est un mensonge en suspend) mais pour l’instant ce qu’ils disent est toujours en accord avec ce qu’ils observent. Et voici en gros ce qu’ils disent (et ce que disait Fourier quand il a étudié la propagation de la chaleur dans un milieu): les opérateurs mathématiques qui décrivent (pour l’instant, jusqu’à ce que quelqu’un dise, fourier s’est un peu planté et sa théorie n’explique qu’une partie des choses et la mienne de théorie est mieux) les phénomènes en question sont telles que les fonctions sinusoïdales et cosinusoïdales facilitent la résolution du problème posé. Ils disent aussi que toute combinaison de ces fonctions que l’on pourrait qualifier de « fondamentales » sont aussi solutions du problème. Sur ce, ils créent un espace mathématique approprié (espace de Hilbert) pour l’ étude des fonctions périodiques, espace qui permet de prouver l’existence, l’unicité de la solution voir la convergence vers d’autres fonctions.
Maintenant considérons le cas de l’onde en dent de scie. Je pense que la question est mal posée. Le problème de savoir POURQUOI fondamentalement l’onde en dent de scie est une combinaison de fonctions sinusoidales est inutile. En effet, quand on se place dans l’espace de Hilbert précédemment créé par les mathématiciens pour mieux comprendre « les choses », il s’avère que l’on peut voir une fonction en dent de scie comme combinaison de sinusoides (un peu comme on peut voir sa position dans l’espace-temps comme trois positions physiques et une position temporelle, si on enlève une donnée de base, (un position physique ou une harmonique), il y a de la perte (on sait moins bien où la personne se trouve, le son est moins riche) ). L’intérêt principal de ce cadre théorique (toute fonction périodique est combinaison de ces sinusoides), c’est qu’il réduit sensiblement les inconnues et qu’il autorise des comparaisons/équivalences entre sons différents puisqu’ils se réduisent tous à un ensemble de sinusoïdes/harmoniques. La réponse au POURQUOI mathématique, c’est que l’intégrale sur une période du produit de la fonction « dent de scie » fois la fonction « sinus d’harmonique n » n’est jamais nulle. Cette intégrale est une mesure de la quantité d’information commune à la « dent de scie » et le « sinus d’harmonique n » (ou d’ordre n). On ressent bien que la partie principale de la dent de scie, si on la regarde de loin peut être vu comme un simple sinus. Ensuite, si on veut aller décrire les coins angulaires, il va falloir des sinus très « serrés ». A mon avis, il n’y a pas d’autres POURQUOI, que le POURQUOI mathématique. De la même manière, il n’y a pour l’instant pas de réponse à la question : « pourquoi le nombre Pi existe-t-il ? », « Pourquoi cette valeur unique qui se retrouve partout dans la nature ?».
Concernant les synthétiseurs, ces fonctions « dent de scie » ou « triangle » ou « marche » sont présentes pour la bonne raison qu’elles sont combinaisons de sinusoides, combinaison dont on sait qu’elle génère un son plus « riche », par expérience. Conceptuellement, il est tout à fait possible de décrire une sinusoïde comme combinaison de fonctions « dent de scie » qui se resserrent (comme les fonctions sinusoïdes se resserrent quand l’harmonique augmente). Dans ce nouvel espace, l’homme dirait : « il est connu qu’un combinaison de fonction « en dent de scie » génère un son pauvre (puisque c’est l’équivalent d’une sinusoïde) et il est préférable de ne conserver qu’une harmonique (de fonction en dent de scie). La perception humaine est toujours la même mais l’explication mathématique/physique est différente parce que l’on est plus dans le même espace. La notion de spectre n’ a de sens que dans l’espace de fourier précédemment défini. Il en aurait un autre (au sens psycho-acoustique) dans un autre espace.
Maintenant au niveau électronique et mécanique, et comme il a été déjà dit, une onde en dent de scie n’est pas plus difficile à générer qu’un sinus (au moins à l’aide d’un ordinateur). Ce qu’il faut plutôt voir, c’est comment la membrane de l’enceinte va être capable de suivre le signal en entrée (la dent de scie donc, ou le sinus) qu’on lui injecte. Ce qui est certain, c’est qu’elle ne suivra jamais une forme en dent de scie parfaite du fait de ses caractéristiques mécaniques. Ce n’est pas pour rien qu’une enceinte est un élément cher et que la recherche dans ce domaine est toujours très active.
Bon je vais arrêter là mais je pense être prêt à affiner certains points si nécessaire. Je pourrais faire une sorte de tutoriel avec code informatique de type Matlab pour montrer les fondements de toutes ces notions.
Pluton
plutonak
En fait, je pense que tout est là dans l'incompréhension de Franco et sa question sur les harmoniques. Il s'avère que la sensation de "chaud", terme qui a été inventé pour définir cette sensation, précède le terme qui la désigne justement. Le feu, en tant que réaction chimique (ou équivalent), génère une sensation. Afin de faciliter la communication et donc PAR DEFINITION, l'homme a décidé de désigner ce phénomène/cette sensation pour le terme chaud/chaude. Par opposition, tout ce qui ne génère pas cette sensation est qualifié de froid/froide. Le feu n'est pas chaud intrinsèquement (la vie n'aime pas trop le feu parce que ça brûle et que ça détruit la vie, mais le reste, sable, métal et tout matière inerte s'en fout !!), il est chaud seulement parce qu'il n'est pas froid.
De la même manière, on postule qu'un sinus de fréquence f prend le nom d'harmonique fondamentale et que tous les sinus de fréquence n*f ou n est un entier, prennent le nom d'harmonique d'ordre n. Par définition donc, un sinus ne contient qu'une harmonique, la fondamentale. Et par constatation et calculs dans les espaces appropriés (espace de Hilbert), une onde en dent de scie contient une infinité d'harmonique dont l'amplitude diminue plus vite que l'augmentation de son ordre (sinon, la somme des harmonique tendrait vers l'infini et ça ferait très mal aux oreilles). Le dent de scie ne contient pas une infinité d'harmoniques intrinsèquement, elle contient une infinité d'harmoniques dans le cadre mathématique défini, accepté, cohérent et utilisé par l'homme. Depuis, il y a eu des extensions à ce cadre, les ondelettes qui ont d'autres caractéristiques intéressantes. Voilà, pour revenir à la question originelle, la fonction scie n'est pas moins ou plus naturelle/ultime qu'un simple sinus. Elle a juste, dans un cadre mathématique bien précis, certaines propriétés que n'a pas un simple sinus.....
au plaisir,
francolamuerte
Merci beaucoup !
Anonyme
Evidemment, comme déjà dit par d'autres, la collection infinie des coefficients Ai est différente pour chaque forme d'onde.
Analogie : la plupart des vecteurs de l'espace ont une composante non nulle sur les 3 axes - seuls quelques uns font exception (par exemple un vecteur parallèle à l'un des axes).
Il y a une infinité possible (non dénombrable) de vecteurs, et par conséquent une infinité de triplets de composantes.
La composante selon un axe est le produit scalaire du vecteur avec le vecteur unitaire sur cet axe.
En revenant à nos moutons de Fourier : les coefficients du spectre sont le produit scalaire de l'onde avec chacune des fonctions trigonométriques qui forment la base de cet espace vectoriel de fonctions (sinus ou exponentielle complexe).
Cet espace vectoriel de fonctions est de dimension infinie, et non plus de dimension 3).
En résumé :
Il n'y a absolument rien d'étonnant à ce qu'une forme d'onde ait une infinité d'harmoniques, c'est le cas de quasiment toutes, sauf quelques exceptions !
francolamuerte
Même si vous dites que ça n'a rien « d'étonnant » il reste,
qu'à l'instar d'André Sauvé, moi
Farots
J'ai trouvé ce topic par hasard, en cherchant sur le net la formule mathématique de la dent de scie, qui est, je l'ai trouvé grâce au grapher de Mac OSX, la somme de tous les [sin(i*x)]/i, pour i entier, allant de 1 à l'infini positif.
Dans son premier post, francolamuerte montre un graphique de la somme de tous les sin(i*x), et en surligne ce qui ressemble à une dent de scie. En observant le spectre de la dent avec l'analyser de Logic, j'ai remarqué que l'intensité des harmoniques de la dent de scie diminue à mesure que leur fréquence augmente. De là, il faut juste multiplier le sinus par l'inverse (1/i) de la fréquence (i*x).
Voilà pour l'infomatif.
Pour répondre plus précisément à la question, quoique, je propose deux chose: On peut considérer la règle "l'onde en dent de scie possède une infinité d'harmoniques décroissants" comme un Axiome, de même que 1+1=2, c'est un "postulat de base" qui permet de rendre applicable -associé à d'autre "postulats de base"- le Théorème de Fourier.
Ok, je vous voit venir en disant "ça ne répond pas à la question".
Je propose donc une autre idée, qui serait de raisonner par la réciproque: démontrer que "une onde possédant une infinité d'harmoniques décroissants est une onde en dent de scie" plutôt que "l'onde en dent de scie possède une infinité d'harmonique décroissants" .
Voilà, en espérant faire avancer ce débat selon moi passionnant.
Dr Pouet
une onde possédant une infinité d'harmoniques décroissants est une onde en dent de scie
Sauf que ce n'est pas tout à fait vrai. Il y a plein de formes d'ondes, pas seulement la dent de scie, qui possèdent une infinité d'harmoniques décroissantes.
En fait, dès qu'il y a une zone anguleuse dans la forme d'onde, et à plus forte raison lorsqu'il y a une discontinuité, il y aura une infinité d'harmoniques. Comme le faisait remarquer quelqu'un au début, "dans ces formes là on ne voit pas trop de sinusoïde". C'est vrai. C'est pour ça qu'il en faut beaucoup et judicieusement paramétrées pour reconstruire cette zone anguleuse.
Farots
Citation de Dr Pouet :
Sauf que ce n'est pas tout à fait vrai. Il y a plein de formes d'ondes, pas seulement la dent de scie, qui possèdent une infinité d'harmoniques décroissantes.
Effectivement, en fait, la définition plus précise est: "une onde possédant l'ensemble des harmoniques entiers décroissants est une onde en dent de scie".
De plus, la théorie sur l'angle me paraît juste, mais elle ne suffit pas à expliquer l'onde en dent de scie, en effet:
- Pourquoi est-ce que le spectre de la saw -qui possède un angle- ne formerait-il pas une onde carré -qui possède aussi un angle-.
- Pourquoi est-ce que l'onde carré possède l'ensemble des harmoniques impaires?
- Pourquoi est-ce qu'une onde possédant l'ensemble des harmoniques multiples de trois forme une autre onde?
Dit autrement, je pense que la question sous-jacente à tout ça est:
- Peut-on -et si oui comment- prévoir la forme d'une onde à partir de son spectre harmonique?
- Et réciproquement, Peut-on -et si oui comment- établir le spectre harmonique d'une onde à partir de sa forme?
Dr Pouet
Effectivement, en fait, la définition plus précise est: "une onde possédant l'ensemble des harmoniques entiers décroissants est une onde en dent de scie".
voire : "une onde possédant l'ensemble des harmoniques entiers N, affectés d'un coefficient en 1/N, est une onde en dent de scie"
sinon on peut certainement obtenir d'autres formes.
Pourquoi est-ce que l'onde carré possède l'ensemble des harmoniques impaires?
Ça je pense qu'on peut le déduire "facilement" (quand on vient de l'étudier en math, c'est évident ; mais 10 ans après...
Dit autrement, je pense que la question sous-jacente à tout ça est:
1. Peut-on -et si oui comment- prévoir la forme d'une onde à partir de son spectre harmonique?
2. Et réciproquement, Peut-on -et si oui comment- établir le spectre harmonique d'une onde à partir de sa forme?
Dans quelques cas simples, on peut le prévoir, sinon non. Il faudra faire le calcul (et généralement de manière numérique, avec un ordinateur).
Dr Pouet
Pourquoi la dent de scie et le rectangle sont les formes d'onde les plus courantes sur les synthétiseurs ?
Dans le contexte originel, donc avec des circuits électroniques analogiques, ces ondes sont très faciles à produire (le rectangle est à peu près un on/off sur une tension continue...). Donc même avec plusieurs oscillateurs et de la polyphonie on reste avec un nombre de composants raisonnables. De plus, il est facile d'en varier la fréquence, ce qui est nécessaire pour passer d'une note à l'autre très rapidement.
Enfin, ces ondes sont très riches en harmoniques, donc avec de simples filtres on peut largement modifier le timbre obtenu.
Finalement c'est quoi des harmoniques ?
En maths, on montre qu'un signal périodique (de fréquence F) peut être reconstitué par une somme de sinusoïdes, d'amplitudes à déterminer, et de fréquences multiples entiers de F. Ces sinusoïdes (à part celle de fréquence F) sont appelées harmoniques.
Or:
- une note, au sens musical, c'est à peu près un signal périodique.
- en mathématiques, on sait faire plein de choses sur les sinusoïdes. Et même sans maths, c'est une représentation qui est finalement assez naturelle.
- d'autant que dans la nature beaucoup de choses correspondent à cette représentation (nos sensations, le comportement d'un condensateur...)
Même si la sinusoïde peut sembler "matheuse" ou "compliquée", ça reste le plus simple et le plus naturel que l'on puisse trouver. Dès que l'on a un cercle, on a des sinus et cosinus. Si on pose un dé sur une platine disque et que l'on regarde depuis le côté la platine tourner, le dé va aller de gauche à droite puis à gauche, et sa position dans le temps correspond à une sinusoïde.
On doit pouvoir décomposer un signal périodique en autre chose qu'une sinusoïde, mais cet autre chose sera plus compliqué.
Pourquoi une onde rectangle ou dent de scie ou triangle a des nombreuses harmoniques ?
Les points anguleux, ou pire, les "coupures" (rectangle ou dent de scie), ou encore pire les asymétries (dent de scie) sont éloignées de la forme de base d'une sinusoïde. Il faut donc additionner de nombreuses sinusoïdes bien choisies pour se rapprocher de ces formes.
Il y a moins d'harmoniques dans un triangle que dans une dent de scie. Dans le triangle on devine déjà assez bien la sinusoïde de base, ce qui n'est pas le cas dans le triangle.
Danguit
"une onde possédant l'ensemble des harmoniques entiers N, affectés d'un coefficient en 1/N, est une onde en dent de scie"
Farots
Citation de Danguit :
Si je ne m'abuse à condition d'avoir la même phase, sinon on trouve n'importe quoi !
C'est vrai qu'on ne l'a pas du tout pris en compte depuis le début du thread -il me semble-, mais je ne sais pas comment se traduit mathématiquement la phase d'un sinus; Quelqu'un aurait-il la réponse?
Danguit
Edit : exemple
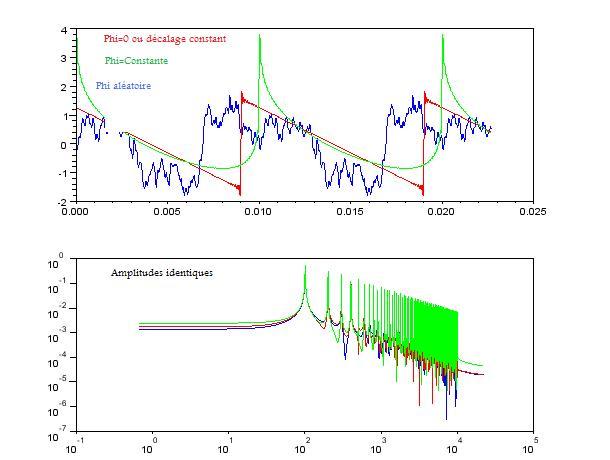
[ Dernière édition du message le 20/04/2011 à 17:47:49 ]
- < Liste des sujets
- Charte
