Sujet Problème de math acoustique :
- 5 réponses
- 4 participants
- 848 vues
- 4 followers
nujazzbes
459
Posteur·euse AFfamé·e
Premier post
Salut !
J'étudie en ce moment les bases de l'acoustique et le chapitre sur lequel je suis porte sur les battements lorsque deux ondes de fréquences proches se superpose.
Je passe les détails du calcul mais le résultat final et que :
s(t) = 2aC'(t)C(t)
- a est l'amplitude du signal.
- C'(t) une fonction cosinus avec une période t.
- C(t) une fonction cosinus avec une période T.
T << t
Et on nous explique que C'(t) va moduler C(t) et ainsi apparaît le phénomène de battement :
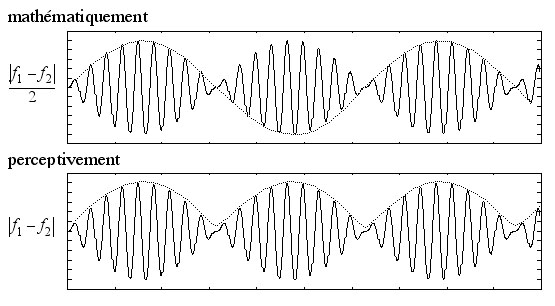
C'est ça que je comprend pas et impossible de trouver quelque chose sur la modulation de deux cosinus.
Ma question pour être plus clair c'est pourquoi c'est l'onde avec la plus basse fréquence qui module celle avec la plus haute.
D'ailleurs on appelle le signal qui module "l'enveloppe", est-ce que on parle d'enveloppe ADSR ou ce sont deux concepts différents ?
J'espère avoir été clair, en fait je suis pas sûr moi même de ce que j'ai pas compris...
Merci
PS : J'ai pas trouvé de rubrique acoustique donc j'ai mis le topic dans synthèse sonore.
J'étudie en ce moment les bases de l'acoustique et le chapitre sur lequel je suis porte sur les battements lorsque deux ondes de fréquences proches se superpose.
Je passe les détails du calcul mais le résultat final et que :
s(t) = 2aC'(t)C(t)
- a est l'amplitude du signal.
- C'(t) une fonction cosinus avec une période t.
- C(t) une fonction cosinus avec une période T.
T << t
Et on nous explique que C'(t) va moduler C(t) et ainsi apparaît le phénomène de battement :
C'est ça que je comprend pas et impossible de trouver quelque chose sur la modulation de deux cosinus.
Ma question pour être plus clair c'est pourquoi c'est l'onde avec la plus basse fréquence qui module celle avec la plus haute.
D'ailleurs on appelle le signal qui module "l'enveloppe", est-ce que on parle d'enveloppe ADSR ou ce sont deux concepts différents ?
J'espère avoir été clair, en fait je suis pas sûr moi même de ce que j'ai pas compris...
Merci
PS : J'ai pas trouvé de rubrique acoustique donc j'ai mis le topic dans synthèse sonore.
<3 <3 <3
srak
4078
Squatteur·euse d’AF
nujazzbes
459
Posteur·euse AFfamé·e
TAMPCO Pedals
3481
Squatteur·euse d’AF
C'est pas facile d'expliquer physiquement ce que de telles ondes donnent. Dans mes cours de physique, on retrouve ce graphe avec la lumière, dans des phénomènes d'interférences. Si tu veux entendre ce que ça donne, tu peux sois sortir un synthé, jouer deux ondes sinusoïdales de fréquence légèrement différentes, soit... ben allumer une radio AM !
Les formules trigonométriques donnent s(t) = a*cos(2pi*f1*t) + a*cos(2pi*f2*t) = 2a*C(t)*C'(t).
En terme de fréquences, on a toujours dans le spectre que deux signaux de fréquences f1 et f2. En revanche, dans le domaine temporel, quand tu superposes les graphes, c'est comme si on multipliait l'amplitude de C par une sinusoïde de fréquence bien plus faible, qu'on appelle enveloppe (ici, C'). On parle de modulation d'amplitude (Amplitude Modulation, en anglais... on parlait de radio ?
).
En pratique, tu vas entendre ton son à peu prêt à la fréquence moyenne de f1 et f2, mais tu entendras aussi des baisses et hausses de volume régulières, ce qui correspond aux minima et aux maxima de l'enveloppe.
L'idée d'enveloppe, tu la retrouve en effet dans l'ADSR ! L'idée est la même, mais au lieu de moduler l'amplitude du signal par un autre (C', sinusoïdal dans l'exemple), tu la fais juste varier suivant des temps d'Attaque, de Decay, de Release différents.
Pour rappel, ADSR signifie Attack Decay Sustain Release
Les formules trigonométriques donnent s(t) = a*cos(2pi*f1*t) + a*cos(2pi*f2*t) = 2a*C(t)*C'(t).
En terme de fréquences, on a toujours dans le spectre que deux signaux de fréquences f1 et f2. En revanche, dans le domaine temporel, quand tu superposes les graphes, c'est comme si on multipliait l'amplitude de C par une sinusoïde de fréquence bien plus faible, qu'on appelle enveloppe (ici, C'). On parle de modulation d'amplitude (Amplitude Modulation, en anglais... on parlait de radio ?
).En pratique, tu vas entendre ton son à peu prêt à la fréquence moyenne de f1 et f2, mais tu entendras aussi des baisses et hausses de volume régulières, ce qui correspond aux minima et aux maxima de l'enveloppe.
L'idée d'enveloppe, tu la retrouve en effet dans l'ADSR ! L'idée est la même, mais au lieu de moduler l'amplitude du signal par un autre (C', sinusoïdal dans l'exemple), tu la fais juste varier suivant des temps d'Attaque, de Decay, de Release différents.
Pour rappel, ADSR signifie Attack Decay Sustain Release
Ancienement appelé The Koala
nujazzbes
459
Posteur·euse AFfamé·e
EraTom
2282
AFicionado·a
- < Liste des sujets
- Charte