Théorie EQ parametrique
- 15 réponses
- 4 participants
- 7 422 vues
- 8 followers
louta
Y aurait-il une bonne âme capable de comprendre l'article en question et d'en expliquer le fonctionnement ici svp
Voila le lien de l'article:
http://www.geofex.com/Article_Folders/EQs/paramet.htm#variable_Q_twin_t
louta
Se schéma est il correcte pour une utilisation studio?

Cpierredon
Ce schéma semble correct.
Mais sa conception laisse à penser qu'il à été conçu en pédale d'effet.
Pour une version studio, je modifierais son alimentation, en l'alimentant en 2X15 volts à l'aide d'une alimentation classique à bade de LM317/LM 327
Ensuite, un tampon en entrés/sortie ne me semble pas inutile, surtout si tu as envie d'entrées/sortie symétriques.
Enfin, je crois que dans ce type de schéma, tu as besoin de potentiomètreslog inversé pour la fréquence ( a voir dans la nomenclature)
http://www.pierredon.free.fr
louta
Je suis en train de traduire complètement le document que j'ai mi en lien. J'aurai probablement besoin d'aide pour vérifier si j'ai pas fait d'erreur dans la retranscription (voir si j'ai pas changé des choses "en mal" dans ma traduction). Je la posterai ici.
Je suis en phase d'apprentissage dans l’électronique et il me manque encore beaucoup de connaissance. Je cherche en se moment à comprendre le fonctionnement (électronique) d'un EQ et des différentes méthode existante pour en fabriquer un paramétrique.
Si vous avez des liens vers des texte qui en parle je suis preneur, merci à tous.
[ Dernière édition du message le 25/06/2014 à 00:27:10 ]
louta
Voici un circuit simple pour commencer la construction de notre contrôle de tonalité.
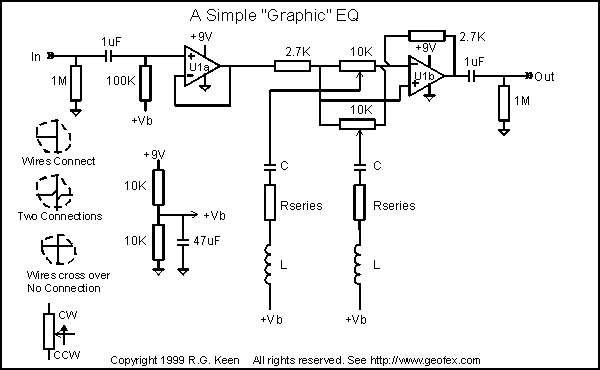
Le circuit est une version simplifiée d'un égaliseur graphique hifi. Sur le schéma si dessus, Il y à deux filtres LC, chacun connectés au curseur d'un des potentiomètres branché en parallèle. Une des caractéristiques d'un filtre LC en série est de présenter une impédance élevée, sauf à sa fréquence de résonance. A cette fréquence, l'impédance série tombe à un minimum, qui est égale à zéro si les composants sont parfaits. La fréquence de résonance peut être calculée comme :
Fr = 1 / (2 * π* √(L * C))
Les potentiomètres sont connectés entre l'entrée inverseuse et l'entrée non-inverseuse d'un amplificateur opérationnel. L'AOP a aussi des résistances d'entrée et de contre réaction.
Le curseur de chaque potentiomètre est relié à la terre au travers de la faible impédance du filtre LC à sa fréquence de résonance. Le curseur du potentiomètre peut être réglé sur l'entrée, auquel cas il shunte l'entrée à la terre, produisant une atténuation dans la réponse en fréquence à sa fréquence centrale. Il peut également être régler vers l'entrée inverseuse, qui shunte le retour à la masse à sa fréquence de résonance, produisant un gain. Lorsque le curseur est au centre, le filtre LC n'a pas d'effet, la réponse en fréquence est plate. Dans cette position, l'effet du filtre LC est égale sur les deux entrées + et -, il n'y a donc pas d'effet global.
Si le filtre LC a une résistance non nulle, il ne ressemble plus à une masse à la fréquence centrale, mais à une résistance. Cela a pour effet de rendre la sélectivité en fréquence moins radicale, le "Q" a été élargie.
Dans la schématique, vous pouvez voir que la configuration est assez simple, un 1er aop tampon devant le montage pour s'assurer qu'il n'y a pas de charge sur la source d'entraînement du circuit et un 2ème aop en sortie, avec les filtres LC liées aux curseurs des potentiomètres monté en parallèle aux entrées du 2ème aop. En ajustant la résistance en série dans chaque section de filtre LC, nous pouvons faire des filtres aussi étroite ou large que nous souhaitons, et nous pouvons ajouter autant de sections de filtre que nous voulons. Le nombre de bandes de fréquence d'un l'égaliseur graphique vont de 5, 7, 10, 20, jusqu'à 31 bandes. Les Q doivent être correctement choisis en fonction de la fréquence centrale de chaque filtres LC. Chaque filtre est indépendant des autres.
Maintenant, nous devons faire en sorte que la fréquence central soit variables. C'est un peu plus difficile. Pour modifier les fréquences de résonance des circuit LC, nous devons changer les valeurs du condensateur (C) ou de l'inductance (L). Bien qu'il existe des condensateurs et des inductances variables, ils sont encombrants et coûteux. Nous devons trouver un moyen de les faire petit et pas cher. Voici une façon de le faire.
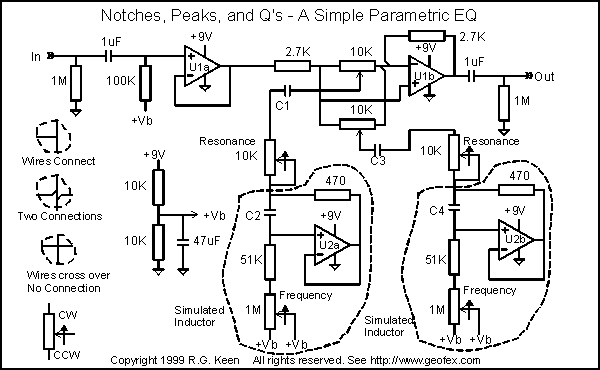
Il existe un circuit qui utilise un AOP, un couple de résistances et un condensateur pour faire un circuit qui ressemble à une bobine d'inductance avec une extrémité à la terre pour le reste du circuit. (Ces circuits sont appelés gyrateurs pour ceux d'entre vous qui veulent creuser plus profond.)
Si nous remplaçons les vrais inductances par les simulations d'inductances, nous obtenons ce qui agit comme une inductance variable. Prenons pour exemple la première simulation de bobine d'inductance représentée sur le schéma. L'inductance est égale à la valeur de C2 multiplié par la valeur de la résistance de 470 ohms (R1 dans la formule) multiplié par la valeur des résistances en série de 51K (R2) + le potentiomètre de 1M (pot).
Ou plus prosaïquement : Leff = R1*(R2+pot)*C
Faisons un peu de mathématiques. Afin de définir la plage de fréquence d'une section LC il nous faut connaître la valeur minimum et maximum de l'inductance.
Avec C2= 0,02µf on a:
Lmin = R1*(R2+pot au minimum)*C2 ici Lmin = 470 * (51K+0)* 0,02µf = 0,4794
Lmax = R1*(R2+pot au maximum)*C2 ici Lmax= 470*(51K+1M) * 0,02µf = 9,8794
(la valeur des résistances sont exprimé en ohms, le condensateur en farad soit pour le calcule de Lmin: 470*51000*0,00000002= 0,4794)
Maintenant nous pouvons définir la valeur minimum et maximum de la plage de fréquences de la section LC en utilisant la formule Fr = 1 / (2 *π* √(L * C))
Avec C1= 0,27µf on a :
fmin= 1/(2*π*√(Lmax*C1)) = 1/(2*π*√(9,8794*0,00000027)) ≈ 97 hz
fmax= 1/(2*π*√(Lmin*C1)) = 1/(2*π*√(0,4794*0,00000027)) ≈ 442hz
(Ses valeurs sont donné à titre indicatif, à vous de trouvez l’équilibre qui correspondent à vos besoin).
Le facteur "Q" de la section du filtre LC est limitée par la résistance équivalente série de l'inductance simulée. La résistance de 470 ohms semble toujours être en série avec l'inductance simulée, nous pouvons donc ajouter une autre résistances externes à l'inductance simulé pour abaisser le Q. C'est la fonction de la commande "résonance". Ce pot vous permet de réduire sensiblement le Q.
Si il y a des erreurs dans se que j'ai traduit n'hésitez surtout pas a le dire.
[ Dernière édition du message le 14/07/2014 à 04:02:46 ]
louta
1 - Qu'est ce que +vb? est ce que c'est la masse?
2 - Que représente cette partie du schéma ?

Rémy M. (chimimic)
Nécessaire pour un montage utilisant des AOP alimentés sous une tension unique (alim non symétrique).
Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com
louta
[ Dernière édition du message le 14/07/2014 à 20:11:27 ]
Rémy M. (chimimic)
Formateur en techniques sonores ; électronicien ; auteur @ sonelec-musique.com
louta
louta
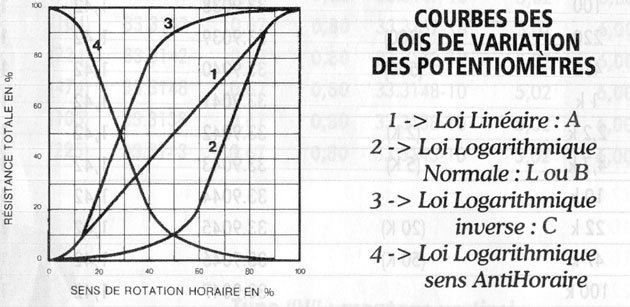
Balley Warson
Sans vouloir dire de bêtise il me semble que la courbe 3 est celle que tu recherches !
Deux questions :
Sur le schema

De bas en haut, le premier potard sert à booster la plage de fréquence choisie
Le second est la largeur de la bande de fréquences et le dernier est fait varier la fréquence choisie ?
Peux t'on n'avoir qu'une bande en supprimant le pot de 10k, c3 et tout ce qu'il y a ensuite (pot de résonance et inductance simulée ) ?
N'importe quel Aop peut il faire l'affaire ? ( ça c'est la question subsidiaire )
Encore merci pour ce partage en tous cas
"Un accord, c'est bien,
deux accords, vous poussez un peu,
trois accords, c'est du Jazz" Lou Reed.
louta
Si la courbe choisi est bien celle que tu dit (la C), alors il y a un truc que je ne comprend pas. Plus les résistance choisi pour simuler l'inductance (dans le schéma 470R et 51K+pot) sont faible, plus la fréquence défini est élevée. La logique voudrai que le potentiomètre tourné vers son minimum nous amène vers les fréquences basse et qu'au contraire plus on le tourne vers son maximum (dans le sens des aiguille d'une montre) plus on vas vers les fréquences aigu hors avec un pot normal (log, anti log ou lin) ça serait l’inverse ou alors il y a un truc qui m’échappe. C'est pour ça que je demandai ici aux personnes qui on de l’expérience.
Pour tes questions, pourquoi veux tu n'avoir qu'une bande, c'est un EQ graphique que tu souhaite faire?
Pour les AOP je n'est pas assez d’expérience pour le dire mais je pense que oui.
[ Dernière édition du message le 24/08/2014 à 10:36:07 ]
Balley Warson
je suis pas sur de saisir ce que tu comprends pas, vu qu'on a un montage du potard en résistance variable y a pas vraiment de sens au montage du potard.
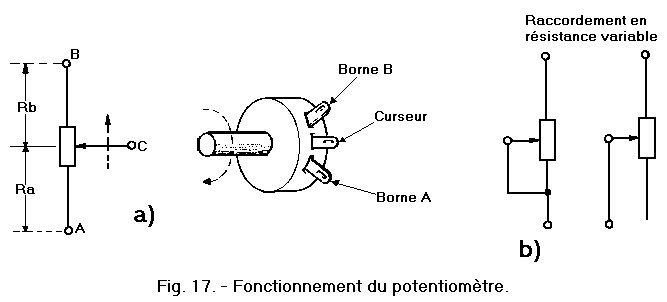
D'ailleurs sur ton schéma les courbes 3,4 sont les reflets l'une de l'autre, tu branches ton potard dans un sens ou l'autre t'as ta courbe 3 ou 4, de 0 à 1M ou de 1M à 0.
Après j'ai peut être pas saisi ce que tu voulais dire ( ce qui est possible ), les équations même si elles n'ont pas l'air bien compliquées je laisse au "pro" le soin de nous explique ça
Je veux qu'une bande pour intégrer cette Eq à un autre effet, et avoir la fréquence avec la plus grande variation possible, sans s'encombrer à rajouter x bandes (de 3 potards ). un peu comme Le Artec SE-PEQ Parametric Equalizer
Les aop, je verrai bien j'essayerai avec ce que j'ai en stock
"Un accord, c'est bien,
deux accords, vous poussez un peu,
trois accords, c'est du Jazz" Lou Reed.
louta
Si tu veux j'ai fait un petit tableur open office pour calculer les fréquence en fonction de la valeur des composant, si tu le veux contact moi par MP.
[ Dernière édition du message le 24/08/2014 à 19:59:40 ]
Balley Warson
"Un accord, c'est bien,
deux accords, vous poussez un peu,
trois accords, c'est du Jazz" Lou Reed.
- < Liste des sujets
- Charte
