113 réponses
21 participants
11 970 vues
20 followers

Anonyme

705

Sujet de la discussion Posté le 13/04/2015 à 12:50:18

Salut salut !

Petite question technique, est-ce qu'il y auras repliement de spectre ou autres problème sur un Master analogique fait à partir d'un fichier 44.1/16 et réenregistré en 192/24 ?

Je me tâte à repasser mes enregistrement 44/16 dans une console haut de game pour chatouillé un peut les preamps et EQs et en faire des fichiers HD 192/24.

Bonne idée, ou fausse bonne idée ?

Bon après si on peut éviter le débat "ça sert à rien de monter plus haut que du 44.1/16 " ce serais cool ! D'ailleurs je n'y crois pas vraiment, mais comme j'aime bien l'idée de repasser mes enregistrement un peut "lofi" dans une console, j'me dit qu'exporter le résultat en 44/16 et en 192/24 ne mange pas de pain, et ça feras des heureux côtés consommateurs de HDaudio...

Merci !

Afficher le sujet de la discussion

fivesstringer

333

Posteur·euse AFfamé·e

Membre depuis 11 ans

26 Posté le 15/04/2015 à 15:25:49

Citation de EraTom :

99.912dB de SNR pour un signal codé sur 16bits...
- Tu as réellement une chaîne audio qui présente un SNR total de 100dB ? Sur quelle largeur de bande mesures-tu la puissance du bruit ?
- Le bruit de quantification sur 16 bits en pleine échelle est de 6.02*16+1.76 = 98.08 dB : Comment peux-tu te retrouver en dessous (sachant que ce bruit va s'ajouter au bruit analogique) ?
- 5dB de perte de SNR, le bit de poids faible en 16bits, en moyenne sur le signal ça me ferait mal... A moins qu'il ne soit déjà noyé dans le bruit.

Il y a un problème de mesure.

C'est clair qu'il ya un loup !!
Quand c'est impossiblement mathématiquement (16 bits et +de 98 dB de SNR) , c'est impossible tout court.
Bravo Eratom pour avoir levé le lièvre. :8O:

Plus important va être de savoir d'où il vient.

Anonyme

9677

27 Posté le 15/04/2015 à 15:35:01

Citation de fivesstringer :

Pas cool il aurait pu, comme il l'avait fait pour un sinus, montrer aussi la tronche d'un signal carré à 10 kHz ou 15 kHz, passé à travers son converto, au lieu de se limiter à 1 kHz...

Si mes souvenirs sont bons, la première harmonique du carré à 10kHz est à 30kHz, celle du carré à 15kHz est à 45kHz. Pour un CAN cadencé à 44,1 ou 48k, un carré à 10kHz est égal à un sinus.

microwAves

3142

Squatteur·euse d’AF

Membre depuis 21 ans

28 Posté le 15/04/2015 à 16:19:49

Hors sujet :

Citation de fivesstringer :
Citation de EraTom :

99.912dB de SNR pour un signal codé sur 16bits...
- Tu as réellement une chaîne audio qui présente un SNR total de 100dB ? Sur quelle largeur de bande mesures-tu la puissance du bruit ?
- Le bruit de quantification sur 16 bits en pleine échelle est de 6.02*16+1.76 = 98.08 dB : Comment peux-tu te retrouver en dessous (sachant que ce bruit va s'ajouter au bruit analogique) ?
- 5dB de perte de SNR, le bit de poids faible en 16bits, en moyenne sur le signal ça me ferait mal... A moins qu'il ne soit déjà noyé dans le bruit.

Il y a un problème de mesure.

C'est clair qu'il ya un loup !!
Quand c'est impossiblement mathématiquement (16 bits et +de 98 dB de SNR) , c'est impossible tout court.
Bravo Eratom pour avoir levé le lièvre.
Plus important va être de savoir d'où il vient.

A un moment dans la vidéo, il explique qu'en fait le fameux "6.02*16+1.76 = 98.08 dB" depend du signal, de mémoire cette formule là est bonne pour les signaux triangulaire.

Bon, j'ai pas el temps de me remettre la vidéo en entier pour retrouver le passage en question, mattez là, elle est hyperinstructive...

marc34.o

1959

AFicionado·a

Membre depuis 16 ans

29 Posté le 15/04/2015 à 19:01:15

Citation :

A un moment dans la vidéo, il explique qu'en fait le fameux "6.02*16+1.76 = 98.08 dB" depend du signal, de mémoire cette formule là est bonne pour les signaux triangulaire.

Très bonne vidéo de Jipihorn qui remet les pendules à l'heure et démontre que la réalité n’est pas aussi simple que la traditionnelle formule 20log10(2^16*√(3/2)) qui n'est qu'une base, pas une vérité absolue.

Le bruit dépend aussi de la forme du signal, des erreurs de numérisation, de la manière dont est traité le signal, et il faudrait aussi ne pas oublier qu'une mesure FFT peut aussi générer de petites erreurs, qu'en fonction de la fréquence (à peine quelques Hz, voire des fractions de Hz suivant la résolution choisie), on peut voir les chiffres de la mesure quelque peu varier, c’est d'ailleurs pour cela que certains logiciels de mesures intègrent une option dans le générateur BF une option nommée "Lock Frequency to FFT", ce qui assurera une plus grande précision en générant une fréquence qui va se caler sur la résolution interne de la FFT.

Les mesures que j'ai produites sont toutes faites dans les strictes mêmes conditions, avec le bon fenêtrage FFT parfaitement adapté à la mesure du SNR. Ca serait d'ailleurs difficile de se tromper, il y a un preset spécial SNR. Et pratiquant la mesure depuis longtemps, c'est pas le genre d'erreur que je fais. Quel que soit le logiciel utilisé, le gené BF utilisé, il peut y avoir de petites différences, mais on est toujours dans des chiffres proches. L'important est que les mesures aient étés toutes faites dans les mêmes conditions, avec le bon paramétrage, ce qui vaut pour valeur de comparaison. Le reste c'est du pinaillage.

En tous cas, la vidéo de Jipihorn est à regarder en intégralité. Elle est peut être pas abordable pour tout le monde, mais de très bonnes explications notamment en ce qui concerne la nature du bruit numérique, comment il se produit, la différence entre rapport signal bruit et dynamique (trop souvent confondus), le principe et l’intérêt de l'oversampling, et quelques mots sur le dithering et les convertisseurs delta sigma.

-----

Calculatrices Audio Android

Open Mind Evénementiel

EraTom

2282

AFicionado·a

Membre depuis 14 ans

30 Posté le 15/04/2015 à 19:16:51

Hors sujet :

Je n'ai pas regardé cette vidéo et Jipihorn n'est pas un mauvais, même s'il n'est pas infaillible comme tout le monde. Il est quand-même plus pointu sur ce qui concerne l'analogique que le numérique.

La formule que j'ai donnée est celle pour un signal sinusoïdale pleine échelle en considérant que l'erreur de quantification suit une densité de probabilité uniforme sur le pas de quantification (le cas "idéal").
Le rapport signal à bruit est alors le rapport entre la puissance de la sinusoïde et la variance du bruit.

La formule exacte du rapport de puissance est (3/2)*2^(2n) ; en dB ça donne bien :
10*log10((3/2)*2^(2n)) = 20*n*log10(2) + 10*log10(3/2) ~ n*6,021 + 3,010

Pour 16bits on obtient ~98,1 dB ; c'est le max, une limite que l'on ne peut pas franchir.

Citation de marc34.o :

C'est une mesure strictement numérique effectuée dans la bande 20/22000Hz, sinus généré par Wavelab directement en 16 bits pour les deux premiers graphique

Ok.
Le bruit de quantification est un bruit blanc dont la puissance totale s'étale sur toute la bande passante ; si tu doubles la fréquence d'échantillonnage le plafond du bruit dans le spectre descend de 3dB mais la puissance totale reste la même (c'est ce qu'exploite un CAN delta-sigma en plus sophistiqué).

Il faut la mesurer sur toute la bande, en partant de 0Hz ; ceci-dit, ça ne suffit pas à expliquer les dB qui manquent. Tu n'aurais pas aussi un banc de filtres réjecteurs centrés sur le fondamentale et les harmoniques ?

Ce qui m'étonne aussi ce sont les disto harmoniques sur une sinusoïde "parfaite" générée en numérique (je veux dire, sans saturation imputable à un étage analogique).

Citation de marc34.o :

il faudrait aussi ne pas oublier qu'une mesure FFT peut aussi générer de petites erreurs,

Tu n'as pas besoin de passer par une FFT : Il suffit de calculer la puissance sur une moyenne temporelle de la différence entre les signaux quantifiés et "idéaux" (i.e avec une quantif très fine dont l'erreur est négligeable).
Le calcul théorique donne la limite "dans le meilleur des mondes" ; tu devrais te retrouver avec un SNR moins bon "dans la vraie vie" et certainement pas meilleur...

[ Dernière édition du message le 15/04/2015 à 19:23:05 ]

marc34.o

1959

AFicionado·a

Membre depuis 16 ans

31 Posté le 15/04/2015 à 20:13:34

Citation :

Le bruit de quantification est un bruit blanc dont la puissance totale s'étale sur toute la bande passante

C’est pas forcément un bruit blanc parfait. C'était d'ailleurs bien expliqué dans la vidéo Digital Show. Ci dessous, le bruit seul généré par le L2 en position type1 et normal.

Le bruit est creusé dans la zone la plus audible vers 3/4Khz et largement boosté au dessus de 16Khz la ou il est quasiment inaudible. Un bruit blanc parfait aurait été une ligne parfaitement plate.

Citation :

si tu doubles la fréquence d'échantillonnage le plafond du bruit dans le spectre descend de 3dB mais la puissance totale reste la même (c'est ce qu'exploite un CAN delta-sigma en plus sophistiqué).

Oui c'est vrai, sauf que tu oublies une chose: ce qui est au dessus de 20Khz n'est pas audible, donc ce qui est au dessus de 20Khz n’est pas pris ne compte dans les standards de mesure. Il y a d'ailleurs la norme AES17 qui comporte, entre autres des standards de niveau, l'utilisation d'un filtre coupant tout ce qu'il y a au dessus de 20Khz (atténuation requise pour satisfaire à la norme: -60dB à 24Khz)
http://www.audiotech.com.tw/AES17%20Filter.htm

Citation :

Il faut la mesurer sur toute la bande, en partant de 0Hz ; ceci-dit, ça ne suffit pas à expliquer les dB qui manquent.

Non: La norme AES17 stipule un filtre qui réjecte les fréquences les plus basses.

Citation :

Ce qui m'étonne aussi ce sont les disto harmoniques sur une sinusoïde "parfaite" générée en numérique (je veux dire, sans saturation imputable à un étage analogique).

Ben apparemment tu n'as jamais vu ce qu'on peut obtenir avec de bons convertisseurs. Accroche toi parce que tu vas être choqué. Ci dessous c'est la mesure d'un processeur de sonorisation utilisant des convertisseurs AKM 24 bits (j'ai plus la référence en tête, mais on les retrouve aussi sur des cartes son RME), mesure en 24bits donc.

Et ne me dis pas cette fois ci que c’est impossible, le magasine sonomag obtient des résultats qui sont comparables aux miens tout comme Jipihorn qui mesure sur un banc Audio Precision.

Citation :

Tu n'as pas besoin de passer par une FFT : Il suffit de calculer la puissance sur une moyenne temporelle de la différence entre les signaux quantifiés et "idéaux" (i.e avec une quantif très fine dont l'erreur est négligeable).

Pour le bruit de fonds, on peut se passer de FFT, mais pour le SNR et le THD, tous les logiciels de mesures utilisent la FFT. Je viens d'essayer de mesurer dans Wavelab le niveau du fichier ne présentant que le dithering du L2, Wavelab affiche bien un mini et maxi RMS, mais refuse d'afficher la moyenne. Donc pas si simple que cela.

Citation :

Le calcul théorique donne la limite "dans le meilleur des mondes" ; tu devrais te retrouver avec un SNR moins bon "dans la vraie vie" et certainement pas meilleur...

c'est ce que j'écrivais, je me cite:

Citation :

Evidemment, si on mesure la même chose en sortie d'un convertisseur 16 bits à partir du même fichier 16 bits, le SNR sera plus faible. Mais le but de la mesure dans un domaine strictement numérique est de mettre en évidence les défauts de la conversion 48/44.1Khz, pas les défauts d'un convertisseur.

-----

Calculatrices Audio Android

Open Mind Evénementiel

[ Dernière édition du message le 15/04/2015 à 20:15:26 ]

Anonyme

8413

32 Posté le 15/04/2015 à 20:18:22

Y'a que moi qui suis complètement largué ? :-D

Anonyme

9677

33 Posté le 15/04/2015 à 20:28:34

Citation de Reno :

Y'a que moi qui suis complètement largué ? :-D

Oui !

Anonyme

8413

34 Posté le 15/04/2015 à 20:35:26

Bon bein je vais me mettre au fond, près du radiateur.... :-D

Anonyme

316

35 Posté le 15/04/2015 à 20:36:59

Nan, c'est ma place. :furieux:

Anonyme

5666

36 Posté le 15/04/2015 à 20:47:23

Citation :

C’est pas forcément un bruit blanc parfait. C'était d'ailleurs bien expliqué dans la vidéo Digital Show. Ci dessous, le bruit seul généré par le L2 en position type1 et normal.

Le bruit est creusé dans la zone la plus audible vers 3/4Khz et largement boosté au dessus de 16Khz la ou il est quasiment inaudible. Un bruit blanc parfait aurait été une ligne parfaitement plate.

Ben c'est plutôt normal, puisque ce n'est pas juste un bruit blanc, mais un bruit de dithering filtré.

EraTom

2282

AFicionado·a

Membre depuis 14 ans

37 Posté le 15/04/2015 à 21:44:11

Hors sujet :

Avant de devenir trop pénible : Je ne cherche pas à t'emmerder mais juste à comprendre la méthode de mesure et les chiffres. -5dB pour le passage de 48kHz à 44.1kHz ça me semble beaucoup d'après mon expérience. J'ai conçu mieux en assez peu d'effort, sans être un surhomme avec mes petits bras, alors ça m'étonne pour un outil comme Wavelab.

Citation :

Le bruit est creusé dans la zone la plus audible vers 3/4Khz et largement boosté au dessus de 16Khz la ou il est quasiment inaudible. Un bruit blanc parfait aurait été une ligne parfaitement plate.

C'est parce que ce n'est pas un bruit de quantification mais un bruit ajouté au dithering (ou encore un bruit mis en forme par une modulation delta-sigma, mais là ça me semble trop important).
Dès que le signal quantifié dépasse à 4 ou 5 bits et que l'on ne tombe pas sur une fréquence tordue qui créerait des erreurs systématiques, l'erreur de quantification se comporte bien comme un bruit blanc.

Citation :

Non: La norme AES17 stipule un filtre qui réjecte les fréquences les plus basses.

Oui mais là c'est un peu hors sujet. On ne cherche pas à estimer ce qui est perçu mais ce qui est générer par les traitements (pour arriver à la conclusion que ce n'est pas perçu, finalement).

Citation :

Ben apparemment tu n'as jamais vu ce qu'on peut obtenir avec de bons convertisseurs.

Si si... Mais je ne comprends pas : Ton signal passe par un CAN où est-ce que tu ne fais que de la synthèse numérique comme tu le disais dans un post précédent (en tout cas c'est ce que j'ai cru comprendre) ?

Citation :

Pour le bruit de fonds, on peut se passer de FFT, mais pour le SNR et le THD, tous les logiciels de mesures utilisent la FFT.

Pour le SNR c'est justement le bruit de fond. Le THD je ne vois pas trop ce qu'il vient faire là si tu génères tout en numérique avec une pure sinusoïde de test (pourquoi les harmoniques alors ?).

Citation :

c'est ce que j'écrivais, je me cite:

Ta première mesure de SNRq sur une quantif à 16bits est proche de 100dB. Ce n'est pas anormal de trouver parfois quelques dixièmes au-dessus de la limite théorique (parce que le signal test n'est pas parfait, il y a des erreurs de calcul dans l'outil, si tu passes par une FFT il y a des biais, etc.) mais 2dB c'est beaucoup pour de la simu numérique.

2dB de plus que la limite théorique et -5dB pour le passage à 44.1kHz, je trouve ça étrange, d'où le questionnement.

Je termine un script de test sous MatLab et je reviens avec des données...

EraTom

2282

AFicionado·a

Membre depuis 14 ans

38 Posté le 15/04/2015 à 22:48:19

Voici ce que j'ai fait :
- Génération de 2 sinusoïdes de fréquence 1347Hz échantillonnées à 44,1kHz et 48kHz en double précision d'une durée de 10 secondes : Ce sont mes sinusoïdes de référence dont le pas de quantif est négligeable devant les pas des quantif 16 et 24 bits;
- Quantifications des sinusoïdes à 16bits et 24bits pleines échelles ;
- Calculs des erreurs par rapports aux sinusoïdes de test puis des SNR en dB en calculant le rapport des puissances sur le temps (on voit ce que ça donne par rapport à la théorie).

Ensuite :
- Interpolation (avec une méthode du pauvre) du signal 24bits @48kHz vers 16bits @44,1kHz avec une précision de calcul en double float;
- Calcul de l'erreur par rapport à la sinusoïde de test et SNR.

Je ne me suis pas occupé des filtres de repliement parce qu'à cette fréquence il n'y en a pas besoin.
Je ne simule pas de disto harmonique.
Pas de dithering parce qu'en pleine échelle et avec ce choix de fréquence il n'y en a pas besoin pour assurer un bruit de quantification uniforme.

Je ne m'intéresse donc qu'à la contribution de l'interpolation.

A noter que je n'utilise pas un bon interpolateur : Il faudrait utiliser celui de Shannon mais j'ai la flemme de me lancer dans son codage.

Je ne prends quand-même pas une interpolation "plus proche voisin" ou "linéaire" qui sont des insultes au traitement du signal audio (et là pour le coup on aurait un post d'erreur de plus de 30dB). J'ai donc choisi les splines, déjà implémentées, qui ont au moins le mérite de pouvoir "lisser" suivant les tangentes à la courbe (je ne vous ai pas menti, ce n'est pas très beau).
Je n'ai pas testé l'interpolation cubic mais avec le phénomène de Runge ça ne doit pas être fameux non plus.

J'ai scripté sous MatLab mais il n'y a pas de fonction exotique ; ça doit aussi tourner avec SciLab qui est gratuit, lui (mais je n'ai pas testé).

Voici les résultats :
SNR quantif 16 bits théorique = 98.0905 dB
SNR quantif 16 bits @44,1kHz = 98.0262 dB
SNR quantif 16 bits @48kHz = 98.1678 dB

SNR quantif 24 bits théorique = 146.2553 dB
SNR quantif 24 bits @44,1kHz = 146.2242 dB
SNR quantif 24 bits @48kHz = 146.2635 dB

SNR quantif 16 bits @44,1kHz à partir du signal 24 bits @48kHz = 97.9536 dB

Et le cadeau bonux :
SNR quantif 16 bits @44,1kHz à partir du signal 16 bits @48kHz = 95.3974 dB (tiens tiens...)
(ce n'est pas le bon ordre, il faut baisser la quantif après avoir sous-échantillonné, sinon on trimbale l'erreur sur le bit de poids faible des 16bits)

Si on ajoutait un bruit, l'interpolation par des splines ne passerait pas aussi bien ; il faudrait faire l'interpolation correcte avec l'interpolateur de Shannon.

Le code pour ceux qui veulent jouer avec (copier/coller) :
close all
clear all
clc

%% Paramètres
Duree = 10; % en secondes

Fe1 = 44100; % en Hz
Fe2 = 48000;

Q1 = 16; % en bits
Q2 = 24;

Freq = 1347; % Fréquence du signal de test en Hz ; choisie pour ne pas être un multiple des Fe

%% SNR Max Théoriques
SNRQ1Th = 10*log10((3/2)*2^(2*Q1));
SNRQ2Th = 10*log10((3/2)*2^(2*Q2));

%% Génération de la sinusoïde de test
NbEchantillons1 = Duree*Fe1;
NbEchantillons2 = Duree*Fe2;

SinusIdealeFe1 = sin((0:1:NbEchantillons1)*(2*pi*Freq/Fe1)); %64 float entre -1 et 1
SinusIdealeFe2 = sin((0:1:NbEchantillons2)*(2*pi*Freq/Fe2));

%% Quantification des sinusoïdes
SinusQ1Fe1 = round(2^(Q1-1)*SinusIdealeFe1)/2^(Q1-1); %Qx-1 car signé, le pas reste de 2^(-Qx).
SinusQ1Fe2 = round(2^(Q1-1)*SinusIdealeFe2)/2^(Q1-1);
SinusQ2Fe1 = round(2^(Q2-1)*SinusIdealeFe1)/2^(Q2-1);
SinusQ2Fe2 = round(2^(Q2-1)*SinusIdealeFe2)/2^(Q2-1);

%% Estimation des erreurs de quantif
ErrQ1Fe1 = SinusIdealeFe1-SinusQ1Fe1;
ErrQ1Fe2 = SinusIdealeFe2-SinusQ1Fe2;
ErrQ2Fe1 = SinusIdealeFe1-SinusQ2Fe1;
ErrQ2Fe2 = SinusIdealeFe2-SinusQ2Fe2;

%% SNR signal à bruit de quantif en dB et affichage des résultats
SNRQ1Th
SNRQ1Fe1 = 10*log10(sum(SinusIdealeFe1.^2)/sum(ErrQ1Fe1.^2))
SNRQ1Fe2 = 10*log10(sum(SinusIdealeFe2.^2)/sum(ErrQ1Fe2.^2))
SNRQ2Th
SNRQ2Fe1 = 10*log10(sum(SinusIdealeFe1.^2)/sum(ErrQ2Fe1.^2))
SNRQ2Fe2 = 10*log10(sum(SinusIdealeFe2.^2)/sum(ErrQ2Fe2.^2))

%% Interpolation Q2 bits Fe2 Hz => Q1 bits Fe1 Hz
%Interpolation avec la précision de calcul de la machine vers la fréquence cible
SinusFloatFe1Interp = interp1((0:1:NbEchantillons2)/Fe2,SinusQ2Fe2,(0:1:NbEchantillons1)/Fe1,'spline');

%Quantification à Q1 bits
SinusQ1Fe1Interp = round(2^(Q1-1)*SinusFloatFe1Interp)/2^(Q1-1);

%Erreur
ErrQ1Fe1Interp = SinusIdealeFe1-SinusQ1Fe1Interp;
SNRQ1Fe1Interp = 10*log10(sum(SinusIdealeFe1.^2)/sum(ErrQ1Fe1Interp.^2))

%% Interpolation Q1 bits Fe2 Hz => Q1 bits Fe1 Hz
%Interpolation avec la précision de calcul de la machine vers la fréquence cible
SinusFloatFe1Interp2 = interp1((0:1:NbEchantillons2)/Fe2,SinusQ1Fe2,(0:1:NbEchantillons1)/Fe1,'spline');

%Quantification à Q1 bits
SinusQ1Fe1Interp2 = round(2^(Q1-1)*SinusFloatFe1Interp2)/2^(Q1-1);

%Erreur
ErrQ1Fe1Interp2 = SinusIdealeFe1-SinusQ1Fe1Interp2;
SNRQ1Fe1Interp2 = 10*log10(sum(SinusIdealeFe1.^2)/sum(ErrQ1Fe1Interp2.^2))

[ Dernière édition du message le 15/04/2015 à 22:49:04 ]

EraTom

2282

AFicionado·a

Membre depuis 14 ans

39 Posté le 15/04/2015 à 23:23:07

Et pour répondre à Danbei :

Voici ce que l'on peut faire comme filtre analogique :
http://www9.dw-world.de/rtc/infotheque/digital_signal/digital_signal_conversion.html

C'est un exemple pour du 44kHz ; la pente tient dans la bande 20-22 kHz sans problème (figure 2.2.2). Il n'y a pas le digramme de phase mais a priori c'est à partir du début de l'atténuation que des bricoles arrivent.
En échantillonnant à 48kHz tu peux faire un filtre qui coupe à partir de 22kHz en atténuant correctement avant 24kHz sans problème (tu prends la même topo et tu calcules les valeurs des composants).

Tu peux numériser en 24bits @48kHz et tu finalises en numérique à 16bits @44kHz en bout de chaîne. L'interpolation introduit moins d'un poil de cu...antif comme erreur ; le filtre numérique est complètement raide avec une phase linéaire jusqu'au bout.

Bref, à l'arriver tu as un spectre nickel plein jusqu'à 22kHz (l'oreille c'est jusqu'à 17kHz, 20kHz pour les oreilles toutes neuves) et des bruits de quantification de l'ordre du pet de mouche.

Et pour ne plus entendre les pets de mouches il est toujours possible de les enfiler en choisissant de bosser en "HD" :bravo:

Danbei

1894

AFicionado·a

Membre depuis 14 ans

40 Posté le 16/04/2015 à 09:39:35

Arg vous m'avez perdu dans vos SNR et compagnie...

Sinon merci pour le lien, simple et instructif.

Citation :

Il n'y a pas le digramme de phase mais a priori c'est à partir du début de l'atténuation que des bricoles arrivent.

, Je pensais que c'était "autour" de la fréquence de coupure ? Donc ça que ça commençait un peu avant...

EraTom

2282

AFicionado·a

Membre depuis 14 ans

41 Posté le 16/04/2015 à 17:27:57

Ben sur les SNR la conclusion est la suivante :

L'erreur d'interpolation due à la décimation de 48kHz vers 44.1kHz est complètement négligeable si l'on part de 24bits pour atteindre 16bits.
Monter à une fréquence multiple de la fréquence cible n'apporte absolument rien de significatif dans ce cas.

Pour le filtre :

Donner une fréquence de coupure "à -3dB" ou un truc dans le genre donne une indication mais ne permet pas de définir un filtre.

Pour définir un filtre (passe-bas) il faut établir un gabarit qui donne :
- La plage de gain dans la bande passante / utile ;
- La plage de gain dans la bande atténuée ;
- La largeur (en fréquence) dans laquelle la courbe de gain passe de la bande utile à la bande atténuée.

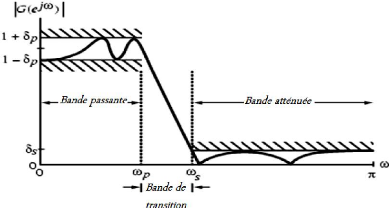
Implantation-dalgorithme-de-filtrage-numerique-sur-FPGAreseau-de-portes-programmables95.png

Implantation-dalgorithme-de-filtrage-numerique-sur-FPGAreseau-de-portes-programmables95.png

La fréquence de coupure à -x dB c'est juste un seul point de passage dans la bande de transition.

En général, un filtre présente un phase quasi-linéaire dans la bande passante. C'est dans la bande de transition que le saut arrive (à moins de concevoir un filtre spécifique). Et dans la bande atténuée... Ben en s'en moque.

marc34.o

1959

AFicionado·a

Membre depuis 16 ans

42 Posté le 16/04/2015 à 18:35:53

Citation :

Citation :
Citation :
Non: La norme AES17 stipule un filtre qui réjecte les fréquences les plus basses.

Oui mais là c'est un peu hors sujet. On ne cherche pas à estimer ce qui est perçu mais ce qui est générer par les traitements (pour arriver à la conclusion que ce n'est pas perçu, finalement).

Les normes sont faites pour que tout le monde fasse la même chose et qu'on puise comparer les mesures. On peut choisir de ne pas les respecter, mais alors dans ce cas la, si on mesure sans filtre AES17, l'oversampling n'augmente plus le SNR si on le mesure une bande passante large, puisque l'over sampling ne fait que déplacer l'énergie du bruit vers le haut. Donc quelqu'un qui mesure sans filtre dira que l'oversamplig n'améliore rien du tout, alors qu'on sait très bien que dans la réalité l'oversampling permet d'augmenter la qualité, puisque la bande passante de nos oreilles est limitée. Pas très cohérent comme raisonnement donc si on n'utilise pas le filtre AES17.

Citation :

Citation :
Citation :
Ben apparemment tu n'as jamais vu ce qu'on peut obtenir avec de bons convertisseurs.

Si si... Mais je ne comprends pas : Ton signal passe par un CAN où est-ce que tu ne fais que de la synthèse numérique comme tu le disais dans un post précédent (en tout cas c'est ce que j'ai cru comprendre) ?

Pour le SNR c'est justement le bruit de fond. Le THD je ne vois pas trop ce qu'il vient faire là si tu génères tout en numérique avec une pure sinusoïde de test (pourquoi les harmoniques alors ?).

Je comprend pas trop ce que tu veux dire. Un sinus, même généré numériquement, engendre des harmoniques, aussi faibles soient elles.

Et puis concernant la FFT, c’est un constat : les logiciels sérieux que je connais utilisent tous la FFT. Même sur un banc Audio Precision qui est la rolls des appareils de mesures, c'est de la FFT qui est utilisé.

Citation :

mais 2dB c'est beaucoup pour de la simu numérique.

Entendons nous bien sur les termes: les graphiques que j'ai produit ne sont pas des simulations mais des mesures réelles d'un signal numérique, signal généré par Wavelab, enregistré en wav, fichier wav lu par le logiciel de mesure. Ce n’est pas une simu venant de matlab ou autres logiciels de ce type. On est bien dans un monde numérique réel, même si tout cela peut paraitre virtuel.

-----

Calculatrices Audio Android

Open Mind Evénementiel

EraTom

2282

AFicionado·a

Membre depuis 14 ans

43 Posté le 16/04/2015 à 20:18:41

Citation de marc34.o :

Les normes sont faites pour que tout le monde fasse la même chose et qu'on puise comparer les mesures. On peut choisir de ne pas les respecter, mais alors dans ce cas la, si on mesure sans filtre AES17, l'oversampling n'augmente plus le SNR si on le mesure une bande passante large, puisque l'over sampling ne fait que déplacer l'énergie du bruit vers le haut. Donc quelqu'un qui mesure sans filtre dira que l'oversamplig n'améliore rien du tout, alors qu'on sait très bien que dans la réalité l'oversampling permet d'augmenter la qualité, puisque la bande passante de nos oreilles est limitée. Pas très cohérent comme raisonnement donc si on n'utilise pas le filtre AES17.

Je ne dis pas que la norme est inutile mais que pour confronter des calculs théoriques à une mesure il faut que les conditions de celle-ci correspondent aux hypothèses de la démonstration théorique, sinon qu'est-ce que l'on teste ?

Pour montrer l'intérêt du sur-échantillonnage je n'ai pas besoin de la norme AES17 : Il suffit de montrer que la puissance totale du bruit de quantification ne dépend pas de la fréquence d'échantillonnage, qu'en sur-échantillonnant au-delà de la bande d'intérêt cette puissance réduite à la bande utile plus étroite est plus faible et que l'on gagne des bits effectifs en sous-échantillonnant.

Quant à la mise en forme du bruit de quantification, elle est effective si l'on place une modulation sigma-delta (qui augmente l'efficacité du sur-échantillonnage).

Citation de marc34.o :

Je comprend pas trop ce que tu veux dire. Un sinus, même généré numériquement, engendre des harmoniques, aussi faibles soient elles.

Euh... Non.

Un sinus parfait ne contient aucune harmonique.

Un sinus généré analogiquement peut contenir des harmoniques à cause des non-linéarités des appareils qui constituent la chaîne.

Un sinus numérique ou quantifié engendre une raie et un bruit uniforme blanc si le nombre de bits effectifs est suffisant et si la fréquence d'échantillonnage n'est pas choisie de manière à provoquer des erreurs de quantification systématiques.
Un signal audio réel contient suffisamment d'aléas pour que l'erreur de quantification soient très proches d'un bruit uniforme (très proche i.e. que les tests statistiques ne fassent pas la différence, alors un instrument de mesure...).
Et si par mégarde on produit en synthèse un signal trop faible pour considérer le bruit comme uniforme, on ajoute une perturbation ==> dithering.

Ça c'est la fft de la sinusoïde quantifiée sur 16 bits à 44,1kHz :

Un doute sur la présence d'harmonique ? Voici la fft de l'erreur de quantification :

Il n'y a rien qui dépasse, on est bien devant le spectre d'un bruit blanc.

Tu dis qu'il est normal d'observer des harmoniques ? Ok mais alors d'où viennent-elles ?

Citation de marc34.o :

Ce n’est pas une simu venant de matlab ou autres logiciels de ce type. On est bien dans un monde numérique réel, même si tout cela peut paraitre virtuel.

Si ce n'est pas un a priori infondé ça... Parce que MatLab n'est pas un outil numérique "réel" ?

Je n'aime pas user de ce genre d'argument, mais mon job est de concevoir et de spécifier des algorithmes de traitement du signal numérique sur des cibles diverses (logiciel, FPGA, etc.) jusqu'à la gestion des quantifications. Le produit fini (en tout cas pour la partie numérique) se comporte au bit près comme le simulateur MatLab.
Cet outil permet justement de vérifier que tout se passe correctement avant la mise en production, en faisant la passerelle entre le calcul théorique sur une feuille de papier et le produit final.

Là pour le coup on peut regarder les normes : Le script que j'ai posté (et que tu peux consulter) génère un sinus avec la fonction de base en float (IEEE Standard 754) puis réalise une simple quantification sur 16bits.
J'avoue ne pas avoir vérifié si la quantif est conforme à la norme IEEE (la bascule sur la valeur médiane) mais ça n'a pas d'importance sur la répartition de l'erreur qui reste dans 2^-16.

Danguit

3348

Squatteur·euse d’AF

Membre depuis 19 ans

44 Posté le 16/04/2015 à 20:40:18

Je suis rassuré de constater que je ne suis pas le seul à me rendre compte que certains font des affirmations fantaisistes et refusent de l'admettre.
En revanche je suis inquiet de constater que sur AF certains modos censurent sans préavis ceux qui veulent le montrer (le WE dernier par exemple suite à un échange avec le même).
De façon générale je me méfie des résultats qui donnent exactement ce que j'espérais et je vérifie par une autre méthode. Mais tout le monde n'a pas la même démarche.
Concernant le S/B, le calcul et une petite simu avec Excel donnent aussi les résultats attendus. Pour être un peu plus rigoureux on pourrait appliquer une correction de bande mais cela ne change pas grand chose.
Pour le filtrage anti-repliement (AN) et de reconstruction (NA), j'ai fait quelques mesures sur des interfaces audio et il semble que pour une machine donnée les deux sont similaires (cf. https://img.audiofanzine.com/image.php?lang=fr&identifier=image&size=normal&module=user&userPhoto_id=282326 et https://img.audiofanzine.com/image.php?lang=fr&identifier=image&size=normal&module=user&userPhoto_id=259862 ).

Passer pour un idiot aux yeux d'un imbécile est une volupté de fin gourmet. (G. Courteline)

FuBiGa

372

Posteur·euse AFfamé·e

Membre depuis 15 ans

45 Posté le 16/04/2015 à 21:00:35

Et cela s'entend ? (quelque part, ce n'est pas le but?)

(ça me fait penser dans le cercle des poètes disparus, qqand le professeur détruit la quantification qualitative d'un poème....)

« 2 + 2 = 5 (pour des valeurs suffisamment grandes de 2) »

EraTom

2282

AFicionado·a

Membre depuis 14 ans

46 Posté le 16/04/2015 à 21:25:26

Citation :

De façon générale je me méfie des résultats qui donnent exactement ce que j'espérais et je vérifie par une autre méthode. Mais tout le monde n'a pas la même démarche.

Je me méfie aussi d'une théorie qu'aucune mesure ne corrobore ou d'une mesure qu'aucune théorie n'est capable d'appréhender : On n'est pas dans les limites de la physique et des connaissances, là.

Dans le cadre du boulot les tests sont multipliés mais ça prend du temps... Pour un échange sur un forum... Bon.
Mais tout de même, par acquit de conscience, tester à l'instant au bout de mon code:


wavwrite(SinusIdealeFe1,Fe1,Q1,'test.wav');
SinusyFe1 = wavread('test.wav')';
ErryFe1 = SinusIdealeFe1-SinusyFe1;
SNRyFe1 = 10*log10(sum(SinusIdealeFe1.^2)/sum(ErryFe1.^2))

Je confie la quantification à la fonction MatLab qui permet d'écrire une fichier .wav puis je l'ouvre et mesure l'erreur.

Le SNR de quantification : 97.9665 dB

L'écart est non significatif certainement dû au seuil de basculement de la troncature.
Les spectres ont la même tête (j'ai la flemme de poster les images), sans harmonique.

A la demande, je peux envoyer le fichier test.wav, mono 16bits @44,1kHz de 10 secondes (c'est long mais ça écarte le problème du fenêtrage)
16*10*44100/(8*1024) = 861 ko

Et là on sera dans le réel ou la simulation ?

Merci pour les mesures Danguit.

Par contre c'est un peu décevant de constater qu'ils n'ont pas resserré le gabarit pour ne rien atténuer jusqu'à 22kHz mais au contraire relâcher la contrainte sur la pente du filtre pour atténuer de 20kHz à 24kHz.
Et pour un CAN 88kHz grand public ça donne quoi ? C'est freestyle de 20kHz à 44kHz ou est-ce que l'on a réellement une bande préservée jusqu'à 40kHz ?

Bon allez, pour le fun : https://www.soundonsound.com/sos/jul12/articles/qanda-0712-1.htm

Citation :

Et cela s'entend ? (quelque part, ce n'est pas le but?)

Franchement, j'aimerais bien pouvoir soumettre ceux qui prétendent entendre une différence à un test en aveugle pour voir s'ils se plantent (pour les cobayes que j'ai pu tester c'était un échec pour leurs oreilles à tous les coups).

Entre 44kHz, 48kHz, 88kHz c'est déjà un sacré pinaillage. Au-delà c'est de la connerie.

[ Dernière édition du message le 16/04/2015 à 21:31:22 ]

trazom

1819

AFicionado·a

Membre depuis 20 ans

47 Posté le 16/04/2015 à 21:30:02

Je n'ai pas tout suivi, mais comment fichtre arrivez-vous à obtenir autant d'harmoniques sur une sinusoïde ?

Si elle est générée numériquement et si toute la chaîne est numérique, à quel moment apparaissent ces harmoniques ?

Remarquez, comme j'ai un peu décroché à un moment, vous pouvez aussi me dire que c'est un peu trop compliqué pour moi.

EraTom

2282

AFicionado·a

Membre depuis 14 ans

48 Posté le 16/04/2015 à 21:32:14

Citation :

comment fichtre arrivez-vous à obtenir autant d'harmoniques sur une sinusoïde ?

Si elle est générée numériquement et si toute la chaîne est numérique, à quel moment apparaissent ces harmoniques ?

Justement, c'est la question. Moi je n'ai rien.

marc34.o

1959

AFicionado·a

Membre depuis 16 ans

49 Posté le 16/04/2015 à 21:47:34

Citation :

Si ce n'est pas un a priori infondé ça... Parce que MatLab n'est pas un outil numérique "réel" ?

Ca n'est pas ce que j'ai dit, juste tout dépend de comment la simulation est faite, et qu'elle ne soit pas une simplification de la réalité.

Citation :

Là pour le coup on peut regarder les normes : Le script que j'ai posté (et que tu peux consulter) génère un sinus avec la fonction de base en float (IEEE Standard 754) puis réalise une simple quantification sur 16bits.

Je vais regarder dés que j'ai un peu de temps.

Citation :

Tu dis qu'il est normal d'observer des harmoniques ? Ok mais alors d'où viennent-elles ?

L’hypothèse la plus probable, serait que le sinus généré par Wavelab ne soit pas parfait, mais il y a bien des harmoniques visibles dans la lecture directe du fichier wav généré par wavelab.

Citation :

A la demande, je peux envoyer le fichier test.wav, mono 16bits @44,1kHz de 10 secondes (c'est long mais ça écarte le problème du fenêtrage)

Je peux le tester dans mon logiciel FFT, et on pourra se rendre compte de la différence qu'il y a entre la mesure FFT et le calcul que tu utilises dans Matlab. Tu peux l'uploader quelque part?

Citation :

Je suis rassuré de constater que je ne suis pas le seul à me rendre compte que certains font des affirmations fantaisistes et refusent de l'admettre.
En revanche je suis inquiet de constater que sur AF certains modos censurent sans préavis ceux qui veulent le montrer (le WE dernier par exemple suite à un échange avec le même).
De façon générale je me méfie des résultats qui donnent exactement ce que j'espérais et je vérifie par une autre méthode.

Tu tombes bien: une vidéo pour toi:

Citation :

Et cela s'entend ? (quelque part, ce n'est pas le but?)

La discussion s'est quelque peu éloigné du débat du début. Une conversion 48/44.1Khz faite avec le bon logiciel et un algo de qualité, il n'y aura pas de différence audible. Mais avec un mauvais algo, il y a des chances que ce soit audible et sur ce site, si on sait interpréter les mesures, on voit bien que tous les logiciels ne se valent pas à ce jeu là: http://src.infinitewave.ca/
Si c'est pour une conversion de 16 bits/44.1Khz vers 24 bits 192Khz, tout le monde est d'accord (pour une fois) pour dire que ça ne sert à rien et ça n'augmente pas la qualité.

-----

Calculatrices Audio Android

Open Mind Evénementiel

EraTom

2282

AFicionado·a

Membre depuis 14 ans

50 Posté le 17/04/2015 à 09:23:00

Ok, je m'en occupe ce soir, mais je n'ai pas de doute sur la fft calculée par MatLab.
Pour info, les graphiques envoyés sont la norme de la transformée discrète en dB. L'axe des fréquences n'est pas en log.

Je peux aussi regarder ce que donne la fft calculée avec MatLab sur le fichier généré par Wavelab.

< Liste des sujets
Charte

Liste des modérateurs

Master en 192/24 d'un WAV en 44.1/16