Pour télécharger Revolverb, venez ici
- 22 réponses
- 5 participants
- 4 163 vues
- 5 followers
Anonyme
Wolfen
De toutes façons, rien n'empêche d'utiliser Revolverb pour faire du monitoring en direct et de mettre SIR pour le mixage et la lecture 
Développeur de Musical Entropy | Nouveau plug-in freeware, The Great Escape | Soundcloud
Anonyme
Citation : rien n'empêche d'utiliser SIR pour faire du monitoring en direct et de mettre SIR pour le mixage et la lecture
Tu t'es mélangé les pinceaux, mais on a bien compris
: Revolverb en direct, SIR en mix et lecture...C'est normal cette différence: le produit de convolution est fait sur un intervalle de temps de -dt à +dt dans SIR, de -dt à 0 dans Revolverb (enfin, ce serait logique).
Wolfen
Citation : Tu t'es mélangé les pinceaux, mais on a bien compris
Pourquoi
Monitoring = un truc en entrée dont on veut entendre le résultat de préférence en même temps...Citation : le produit de convolution est fait sur un intervalle de temps de -dt à +dt dans SIR, de -dt à 0 dans Revolverb (enfin, ce serait logique).
T'as des sources pour ça ? Jamais entendu parler... En plus ça me semble bizarre comme truc sachant que le produit de convolution n'est JAMAIS fait sur le domaine temporel, mais plutôt sur des paquets d'échantillons traité dans le domaine fréquentiel via une FFT, auquel on applique ensuite une FFT inverse pour obtenir le résultat du calcul. Je pense plutôt que les différences sonores proviennent des diverses simplifications des calculs nécessaires pour optimiser la latence au maximum.
Développeur de Musical Entropy | Nouveau plug-in freeware, The Great Escape | Soundcloud
Anonyme
Citation : Monitoring = un truc en entrée dont on veut entendre le résultat de préférence en même temps...
Ben justement, Revolverb qui n'a pas de latence me parait plus adaptée que SIR qui en présente une ?
Citation : des paquets d'échantillons traité dans le domaine fréquentiel via une FFT
Ta FFT, elle est forcément faite en traitant un intervalle de temps: une analyse spectrale par définition n'a pas de sens à un instant t.
[Edit
La transformée de Fourier (la vraie) est calculée par une intégrale de - l'infini à + l'infini sur t:
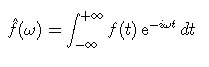
La FFT est calculée sur un nombre donné d'échantillons, qui correspondent à un intervalle de temps.[/edit]
Mon interprétation du fait que revolverb ne présente pas de latence, c'est que la FFT est calculée sur l'intervalle de temps qui précède l'instant courant, et que SIR le fait peut-être sur un intervalle du type [-dt, +dt], ce qui impliquerait alors automatiquement une latence.
Wolfen
Par contre sur la fin j'enfonce le clou, la FFT ne se fait pas par convolution, puisque l'intérêt d'utiliser la FFT c'est pour simplifier le calcul de la convolution dans le domaine fréquentiel
En fait, la FFT est basée sur un algorithme assez complexe (dont on peut avoir quelques explications dans la page de liens du dossier) et elle s'applique toujours à un paquet d'échantillons donné (par exemple disons 512 échantillons), cette taille déterminant la latence du procédé.Pour les histoires de zéro latence, apparemment c'est basé sur le fait que le calcul peut être effectué pendant le temps de latence de la carte son... Mais j'en sais pas beaucoup plus
Développeur de Musical Entropy | Nouveau plug-in freeware, The Great Escape | Soundcloud
Anonyme
Mais si je prends le temps d'être sérieux, je dois encore être capable de comprendre le détail du truc: j'ai parcouru en diagonale ce matin, et ça a l'air hyper intéressant. Et comme en plus ça sonne, d'après les qq essais que j'ai fait, ben je pense que je vais me convertir à cette approche. J'ai entendu dire le plus grand bien des impulses de baffles, et ça me branche pas mal, ça.
Un jour, on aura les impulses de Freddie Mercury et Robert Plant. Et là, je pourrai chanter
Anonyme
Citation : Il y a une chose à retenir sur la formulation des FFT, qu'on ne trouve pas avec celle du produit de convolution basique, c'est que le calcul du signal de sortie à un instant donné nécessite la connaissance du signal d'entrée à cet instant et à des instants supérieurs, du fait du passage d'une représentation amplitude/temps à une représentation amplitude/fréquence...
SIR est certainement basé sur un algorithme normal, qui calcule la FFT à un instant t sur des échantillons répartis de t-dt à t+dt : c'est le truc normal, on centre l'intervalle de temps sur l'instat de référence.
Pour contourner ce problème de l'anticipation temporelle, il y a une astuce, elle aussi classique, qui consiste à calculer la FFT seulement à partir de la partie [t-dt,t]. Le résultat est moins précis, mais permet d'éviter la latence intrinsèque de l'algorithme. C'est peut-être ce qui a été utilisé dans Revolverb Lite, et qui expliquerait pourquoi le son est plus pracis avec SIR.
On retrouve ces atsuces de décalage d'intervalle dans tous les traitements numériques en fait, que ce soit dans le son ou dans le domaine de l'image, le cas le plus flagrant étant les algorithmes de poursuite radar (là, il ne s'agit de prédiction, pas de FFT, mais il y a des similitudes).
Ca me rassure, même 20 ans après, j'ai de beaux restes
Anonyme
Ca ne s'invente, pas des trucs comme ça...
Wolfen
Citation : Pour contourner ce problème de l'anticipation temporelle, il y a une astuce, elle aussi classique, qui consiste à calculer la FFT seulement à partir de la partie [t-dt,t]. Le résultat est moins précis, mais permet d'éviter la latence intrinsèque de l'algorithme. C'est peut-être ce qui a été utilisé dans Revolverb Lite, et qui expliquerait pourquoi le son est plus pracis avec SIR.
Ca me laisse dubitatif cette histoire
Si c'était aussi simple, tous les plug-ins seraient équipés de cette technique et en plus j'en ai jamais entendu parler dans toutes les pages sur les algos de FFT que j'ai lues. C'est vrai que ça paraît logique (quoique ça empêche de déterminer le calcul sur des paquets qui suivent des silences). Faudrait que je creuse le sujet...Développeur de Musical Entropy | Nouveau plug-in freeware, The Great Escape | Soundcloud
- < Liste des sujets
- Charte