Propriétés physique en champ libre
- 37 réponses
- 5 participants
- 3 555 vues
- 9 followers
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
Sujet de la discussion Posté le 25/03/2016 à 23:22:11Propriétés physique en champ libre
Bonjour,
Je suis étudiant en deuxième année de classe préparatoire et dans le cadre d'un projet (TIPE) j'ai pour objectif de déterminer par une modélisation informatique le position optimal de hauts-parleurs dans une salle donnée en prenant en compte les réflexions du son sur les murs. Pour ce faire, j'ai créé un programme qui me permet de calculer de façon récursive les différentes réflexions sur les murs, lorsque l'on place un haut parleur à un endroit donné.
Néanmoins, j'ai quelques question d'un point de vue théorique :
Dans ma modélisation, je me place en champ libre. J'ai lu à plusieurs endroits que dans ce cas, si l'on a deux sources, les intensités sonores s'additionnent. Ma prof de physique a émit quelques réserves sur cela en disant que, dans le cas de sources monochromatiques, les surpressions s'additionnent, mais que, pour un son complet, qui a presque un spectre continu, je devais prouver que cette affirmation reste vraie.
Autre question : Comment peut-on démontrer que, pour une onde acoustique, la réflexion des ondes suit une loi similaire aux lois de Descartes en optique ?
Auriez-vous des conseils sur le sujet ?
Merci d'avance !
Cordialement
Je suis étudiant en deuxième année de classe préparatoire et dans le cadre d'un projet (TIPE) j'ai pour objectif de déterminer par une modélisation informatique le position optimal de hauts-parleurs dans une salle donnée en prenant en compte les réflexions du son sur les murs. Pour ce faire, j'ai créé un programme qui me permet de calculer de façon récursive les différentes réflexions sur les murs, lorsque l'on place un haut parleur à un endroit donné.
Néanmoins, j'ai quelques question d'un point de vue théorique :
Dans ma modélisation, je me place en champ libre. J'ai lu à plusieurs endroits que dans ce cas, si l'on a deux sources, les intensités sonores s'additionnent. Ma prof de physique a émit quelques réserves sur cela en disant que, dans le cas de sources monochromatiques, les surpressions s'additionnent, mais que, pour un son complet, qui a presque un spectre continu, je devais prouver que cette affirmation reste vraie.
Autre question : Comment peut-on démontrer que, pour une onde acoustique, la réflexion des ondes suit une loi similaire aux lois de Descartes en optique ?
Auriez-vous des conseils sur le sujet ?
Merci d'avance !
Cordialement
- 1
- 2
EraTom
2282
AFicionado·a
Membre depuis 15 ans
26 Posté le 14/04/2016 à 09:48:01
Citation de Imlach :
Oui. Le niveau d'émission est celui du HP monté sur l'enceinte atténué de 3dB sur les lignes du diagramme.D'accord, donc il faut que je travaille avec la même surface que sur le diagramme de directivité, sur laquelle je dispose des sources ponctuelles, dont le niveau d’émission est fonction des valeurs du diagramme de directivité. J'ai bien tout compris ?
N'oublie pas la phase...
Citation :
Je ne comprends pas ton interrogation... En fait j'ai l'impression, mais je me trompe peut-être, que tu cherches à propager des intensités, puis gérer les interférences.J'ai commencé à coder la partie permettant de gérer les interférences. Pour les interférences avec plus de deux sources, on peut les traiter les unes après les autres ou il y a des formules spéciales ? J'ai un peu de mal à trouver des infos
Comme je te le dis depuis le début, ce qu'il faut estimer c'est la valeur des champs p et b (ou phi tout seul) car ce sont eux qui se superposent.
En un point M tu calcules la valeur des champs p et v pour chaque sources ponctuelles (que tu auras placées sur les surfaces de chaque source "réelle"), puis tu fais la somme de tous les champs p et v...
Pour chaque source ponctuelle tu as normalement calculé la valeur du champ en M en prenant en compte l'atténuation et la phase (parce que tu ne peux pas faire autrement !).
Donc quand tu en fais la somme les interférences sont calculées, puis tu en déduis l'intensité totale reçue.
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
27 Posté le 14/04/2016 à 09:51:44
Enfin, plutôt que de placer des sources ponctuelles le long du diagramme, pourquoi ne places-tu pas les sources sur la membrane, directement ?...
0
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
28 Posté le 14/04/2016 à 11:58:46
Citation :
Je ne comprends pas ton interrogation... En fait j'ai l'impression, mais je me trompe peut-être, que tu cherches à propager des intensités, puis gérer les interférences.
J'ai bien compris qu'il fallait travailler avec les champs.
Et si j'ai posé cette question, c'est parce que, dans le programme que j'ai fait, le meilleur moyen que j'ai trouvé pour modéliser le problème c'est d'utiliser, pour chaque champ deux variables pour chaque point de l'espace : une contenant l'amplitude, et l'autre la phase. Et donc, si je souhaite additionner deux champs, il me faut réussir à calculer l'amplitude et la phase résultante...
Citation :
Enfin, plutôt que de placer des sources ponctuelles le long du diagramme, pourquoi ne places-tu pas les sources sur la membrane, directement ?...
En effet, ce serait plus intuitif...
Mais j'ai deux problèmes avec ça :
1 - Si je place des sources au niveau de la membrane, je fais abstraction des autres éléments qui composent le haut-parleur. Et notamment, j'obtiendrais sans doutes un niveau sonore derrière l'enceinte qui est plus important qu'en réalité. En utilisant le diagramme de directivité, je suppose que les mesures permettant de l'obtenir ont été faites avec le haut-parleur complet, et non juste la membrane, ce qui résout le problème.
2 - Avec le diagramme de directivité, il me suffit de mesurer expérimentalement le niveau sonore en 1 point de l'espace pour ensuite le calculer simplement sur toute la surface, et donc cela me permet d'avoir des valeurs initiales. Mais avec la membrane, j'ai un peu de mal à voir comment je peux obtenir des valeurs initiales expérimentalement.
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
29 Posté le 14/04/2016 à 13:37:41
J'ai l'impression que tu te retrouves coincé dans une mauvaise solution. Tu touches du doigt ce qui arrive lorsque l'on prend "les choses à l'envers" comme je te l'indiquais.
Le problème c'est que la nature et la physique, qui tente de la modéliser, ne s'adapteront pas à ton algo... Surtout qu'elles font les choses plus simplement.
Comment ça "une amplitude et une phase" ? pour représenter la direction il en manque (à moins que tu sois passé par le potentiel phi ?).
Je ne comprends pas ton problème ; pour une seule source ponctuelle ton programme n'est-il pas capable de calculer p et v en chaque point à chaque instant (en passant par un paramétrage par une amplitude et une phase si ça te chante) ?
Si oui, et j'espère bien que c'est la cas, pour N sources tu calcules N champs p et N champs v (par N amplitudes et N phases) et... Tu fais la somme des N champs p et N champs v en chaque point et chaque instant pour obtenir les champs totaux, avec les interférences en conséquences.
Le problème c'est que la nature et la physique, qui tente de la modéliser, ne s'adapteront pas à ton algo... Surtout qu'elles font les choses plus simplement.
Citation :
Si tu souhaites additionner deux champs... Tu en fais la somme en chaque point et en chaque instant.une contenant l'amplitude, et l'autre la phase. Et donc, si je souhaite additionner deux champs, il me faut réussir à calculer l'amplitude et la phase résultante...
Comment ça "une amplitude et une phase" ? pour représenter la direction il en manque (à moins que tu sois passé par le potentiel phi ?).
Je ne comprends pas ton problème ; pour une seule source ponctuelle ton programme n'est-il pas capable de calculer p et v en chaque point à chaque instant (en passant par un paramétrage par une amplitude et une phase si ça te chante) ?
Si oui, et j'espère bien que c'est la cas, pour N sources tu calcules N champs p et N champs v (par N amplitudes et N phases) et... Tu fais la somme des N champs p et N champs v en chaque point et chaque instant pour obtenir les champs totaux, avec les interférences en conséquences.
0
[ Dernière édition du message le 14/04/2016 à 13:42:35 ]
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
30 Posté le 14/04/2016 à 21:58:11
ah oui...
En gros moi j'étais parti du principe que, comme on a quelque chose de la forme a*(wt + phi), si je déterminer en chaque point le a et le phi, après je peux le calculer pour tout t très facilement...
Mais effectivement, c'est pas le plus simple au final.
En fait, je finis par m'embrouiller avec tout ça, et notamment sur ce que j'ai le droit dire.
Concrètement, pour une source ponctuelle acoustique, elle est définie par son vecteur position, sa pression initiale, sa vitesse de propagation initiale. Et, toujours si j'ai bien compris, et si je me plante pas, avec une source ponctuelle, l'expression de ces grandeurs est de la forme P0/|r-r0|*cos(k|r-r0| - wt).
C'est bien cela ? Ou alors je suis complétement à coté de la plaque...
En gros moi j'étais parti du principe que, comme on a quelque chose de la forme a*(wt + phi), si je déterminer en chaque point le a et le phi, après je peux le calculer pour tout t très facilement...
Mais effectivement, c'est pas le plus simple au final.
Citation :
Je ne comprends pas ton problème ; pour une seule source ponctuelle ton programme n'est-il pas capable de calculer p et v en chaque point à chaque instant (en passant par un paramétrage par une amplitude et une phase si ça te chante) ?
En fait, je finis par m'embrouiller avec tout ça, et notamment sur ce que j'ai le droit dire.
Concrètement, pour une source ponctuelle acoustique, elle est définie par son vecteur position, sa pression initiale, sa vitesse de propagation initiale. Et, toujours si j'ai bien compris, et si je me plante pas, avec une source ponctuelle, l'expression de ces grandeurs est de la forme P0/|r-r0|*cos(k|r-r0| - wt).
C'est bien cela ? Ou alors je suis complétement à coté de la plaque...
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
31 Posté le 16/04/2016 à 16:20:21
Le champs "v" n'est pas la vitesse de propagation de l'onde mais une variation locale de la position d'un volume élémentaire du fluide, de moyenne nulle.
La vitesse de propagation a par contre bien la même direction que v.
Oui, la formule que tu donnes et bien l'une des solutions de l'équation d'onde pour le problème sphérique monochromatique.
Note qu'en fonction du signe sur l'argument du cos tu obtiens une onde progressive ou une onde rétrograde ; en sommant ces deux solutions tu obtiens une onde stationnaire (tu as dû le voir en electromag).
La vitesse de propagation a par contre bien la même direction que v.
Oui, la formule que tu donnes et bien l'une des solutions de l'équation d'onde pour le problème sphérique monochromatique.
Note qu'en fonction du signe sur l'argument du cos tu obtiens une onde progressive ou une onde rétrograde ; en sommant ces deux solutions tu obtiens une onde stationnaire (tu as dû le voir en electromag).
0
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
32 Posté le 10/05/2016 à 23:12:38
Bonjour,
En raison des épreuves écrites je n'ai pas pu pleinement me concentrer sur mon TIPE, mais maintenant que ces épreuves sont finis, je suis pleinement opérationnel.
J'ai désormais réalisé un programme qui me permet de définir un certain nombre de sources ponctuelles, réparties selon un certain schéma en 3D (qui pourra être édité via un logiciel de modélisation 3D), et prenant comme paramètres des valeurs initiales pour la vitesse et la surpression.
Maintenant, et au vu de ce qui a été dis précédemment, il semble que j'ai deux possibilités :
- Soit je m’intéresse à la membrane du haut parleur et réparti mes sources ponctuelles sur cette surface.
- Soit j'utilise un diagramme de directivité, que je transforme en figure 3D.
Dans le premier cas, je reste assez septique dans la mesure où cela ne prends pas en compte ce qui entoure la membrane (cad le caisson), et donc cela ne reflète pas le propagation du son pour un haut parleur, mais juste pour sa membrane seule.
Dans le deuxième cas, ce problème ne se pose plus, car le diagramme a été réalisé avec le haut parleur complet, mais le problème vient cette fois de l'obtention de ce diagramme, qui nécessite un certain matériel, ce qui rend la comparaison entre modélisation et expérimentation plus difficile.
Selon vous, quelle est la modélisation la plus viable ?
Autre chose : Une fois cette surface modélisée, et une fois les sources positionnées sur cette surface, comment déterminer les constantes liées à chaque source (cad V0 et µ0) pour chaque source, car ce sont ces valeurs qui me permettront de concrétiser mon travail en réalisant par exemple une image représentant le niveau sonore en différents points de l'espace ?
Merci d'avance
En raison des épreuves écrites je n'ai pas pu pleinement me concentrer sur mon TIPE, mais maintenant que ces épreuves sont finis, je suis pleinement opérationnel.
J'ai désormais réalisé un programme qui me permet de définir un certain nombre de sources ponctuelles, réparties selon un certain schéma en 3D (qui pourra être édité via un logiciel de modélisation 3D), et prenant comme paramètres des valeurs initiales pour la vitesse et la surpression.
Maintenant, et au vu de ce qui a été dis précédemment, il semble que j'ai deux possibilités :
- Soit je m’intéresse à la membrane du haut parleur et réparti mes sources ponctuelles sur cette surface.
- Soit j'utilise un diagramme de directivité, que je transforme en figure 3D.
Dans le premier cas, je reste assez septique dans la mesure où cela ne prends pas en compte ce qui entoure la membrane (cad le caisson), et donc cela ne reflète pas le propagation du son pour un haut parleur, mais juste pour sa membrane seule.
Dans le deuxième cas, ce problème ne se pose plus, car le diagramme a été réalisé avec le haut parleur complet, mais le problème vient cette fois de l'obtention de ce diagramme, qui nécessite un certain matériel, ce qui rend la comparaison entre modélisation et expérimentation plus difficile.
Selon vous, quelle est la modélisation la plus viable ?
Autre chose : Une fois cette surface modélisée, et une fois les sources positionnées sur cette surface, comment déterminer les constantes liées à chaque source (cad V0 et µ0) pour chaque source, car ce sont ces valeurs qui me permettront de concrétiser mon travail en réalisant par exemple une image représentant le niveau sonore en différents points de l'espace ?
Merci d'avance
0
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
33 Posté le 14/05/2016 à 23:50:11
Bonjour,
Voici les derniers avancements :
J'ai finalement décidé de travailler avec les membranes directement, donc sans passer par les diagrammes de directivité.
Au niveau des constantes, j'ai réglé le problème de façon assez simple au final.
En gros, il y avait deux constantes inconnues pour les sources à placer sur la membrane : la constante multiplicative et la constante liée à la phase.
Pour la phase, j'ai fait l’hypothèse que tous les points de la membrane bougent en même temps, donc j'ai mis cette constante à 0 pour chaque source.
Pour la constante multiplicative, je me suis rendu compte que, lorsque je passe au calcul du niveau sonore, cette constante multiplicative se transforme simplement en une constante additive, qui ne m’intéresse pas, dans la mesure où je m’intéresse plus aux variations du niveau sonore, qu'à des valeurs en tant que telles.
J'ai codé la partie permettant de modéliser la membrane grâce à un logiciel de modélisation 3D.
J'ai également codé la partie graphique qui permet de visualiser sous la forme d'une image le résultat de la modélisation.
Le temps de calcul est tout de même très important...
Mais voici tout de même quelques résultats que j'ai obtenu :
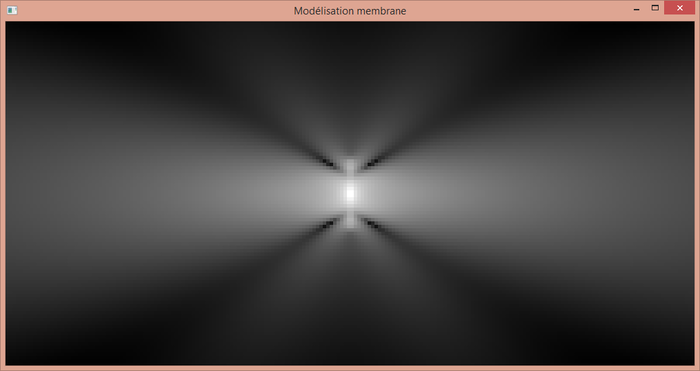
Il s'agit du résultat pour une membrane de forme ovale.
Le résultat est intéressant, et on voit bien des zones d'interférences destructives.
Je test d'autres formes de membranes, mais les résultats sont moins intéressant...
Que pensez-vous de ces résultats ?
Cela semble-t-il cohérent ?
Quels formes "intéressantes" puis-je essayer ?
Merci d'avance
Voici les derniers avancements :
J'ai finalement décidé de travailler avec les membranes directement, donc sans passer par les diagrammes de directivité.
Au niveau des constantes, j'ai réglé le problème de façon assez simple au final.
En gros, il y avait deux constantes inconnues pour les sources à placer sur la membrane : la constante multiplicative et la constante liée à la phase.
Pour la phase, j'ai fait l’hypothèse que tous les points de la membrane bougent en même temps, donc j'ai mis cette constante à 0 pour chaque source.
Pour la constante multiplicative, je me suis rendu compte que, lorsque je passe au calcul du niveau sonore, cette constante multiplicative se transforme simplement en une constante additive, qui ne m’intéresse pas, dans la mesure où je m’intéresse plus aux variations du niveau sonore, qu'à des valeurs en tant que telles.
J'ai codé la partie permettant de modéliser la membrane grâce à un logiciel de modélisation 3D.
J'ai également codé la partie graphique qui permet de visualiser sous la forme d'une image le résultat de la modélisation.
Le temps de calcul est tout de même très important...
Mais voici tout de même quelques résultats que j'ai obtenu :

Il s'agit du résultat pour une membrane de forme ovale.
Le résultat est intéressant, et on voit bien des zones d'interférences destructives.
Je test d'autres formes de membranes, mais les résultats sont moins intéressant...
Que pensez-vous de ces résultats ?
Cela semble-t-il cohérent ?
Quels formes "intéressantes" puis-je essayer ?
Merci d'avance
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
34 Posté le 15/05/2016 à 13:18:45
Salut,
Je suis en plein déménagement et je n'ai plus autant de temps qu'avant pour les réponses ; je vais succinct.
Tout d'abord, ce que tu obtiens en propageant semble cohérent et c'est encourageant
Les deux interférences destructives sur les côtés correspondent bien à ce que l'on a quand la taille de la membrane n'est pas négligeable devant longueur d'onde.
Diminue la fréquence et elles doivent disparaitre.
En revanche il me semble que ton modèle de membrane n'est pas correct (au-delà de l'initialisation) :
- Quand la membrane pousse l'air sur une face elle "aspire" l'air sur l'autre ;
- De part et d'autre de la membrane du HP tu obtiens des ondes en opposition d'amplitude (pas simplement déphasée de pi même si c'est équivalent en régime sinusoïdale établi) ;
- Du coup, les ondes propagées de part et autre s'annulent lorsqu'elle se rencontrent : C'est ce que l'on appelle le court-circuit acoustique.
Je t'invite à lire le pdf que je t'avais mis en lien qui explique ceci et pourquoi l'on arrive à l'enceinte :
- Pour éviter le court-circuit on place la membrane du HP (et donc le HP) sur en "plan infini" (dans la pratique, très grand) qui sépare l'espace en deux et évite que les ondes des faces arrière et avant du HP interférent : On a coupé le court-circuit acoustique ;
- Comme on ne peut pas se balader avec une planche de 10m par 10m, on enferme l'arrière du HP dans une boîte qui va contenir les ondes de la face arrière : C'est l'enceinte close.
De ton côté il faudrait que tu trouves un moyen de ne pas compter l'émission arrière.
Je suis en plein déménagement et je n'ai plus autant de temps qu'avant pour les réponses ; je vais succinct.
Tout d'abord, ce que tu obtiens en propageant semble cohérent et c'est encourageant
Les deux interférences destructives sur les côtés correspondent bien à ce que l'on a quand la taille de la membrane n'est pas négligeable devant longueur d'onde.
Diminue la fréquence et elles doivent disparaitre.
En revanche il me semble que ton modèle de membrane n'est pas correct (au-delà de l'initialisation) :
- Quand la membrane pousse l'air sur une face elle "aspire" l'air sur l'autre ;
- De part et d'autre de la membrane du HP tu obtiens des ondes en opposition d'amplitude (pas simplement déphasée de pi même si c'est équivalent en régime sinusoïdale établi) ;
- Du coup, les ondes propagées de part et autre s'annulent lorsqu'elle se rencontrent : C'est ce que l'on appelle le court-circuit acoustique.
Je t'invite à lire le pdf que je t'avais mis en lien qui explique ceci et pourquoi l'on arrive à l'enceinte :
- Pour éviter le court-circuit on place la membrane du HP (et donc le HP) sur en "plan infini" (dans la pratique, très grand) qui sépare l'espace en deux et évite que les ondes des faces arrière et avant du HP interférent : On a coupé le court-circuit acoustique ;
- Comme on ne peut pas se balader avec une planche de 10m par 10m, on enferme l'arrière du HP dans une boîte qui va contenir les ondes de la face arrière : C'est l'enceinte close.
De ton côté il faudrait que tu trouves un moyen de ne pas compter l'émission arrière.
0
- Krom -
391
Posteur·euse AFfamé·e
Membre depuis 15 ans
35 Posté le 15/05/2016 à 13:26:45
Flag, super intéressant comme sujet de TIPE ! Bon courage !
0
Imlach
28
Nouvel·le AFfilié·e
Membre depuis 10 ans
36 Posté le 15/05/2016 à 14:44:00
Ok... Je me disais bien que c'était bizarre ce qui se passait à l'arrière de la membrane.
Ça va vraiment pas être simple de ne pas gérer la partie arrière... Parce que même si c'est simple à faire avec une membrane plane, si je prends une membrane conique, c'est déjà plus compliqué.
Mais je vais bien trouver une solution...
Je continuerais de poster pour expliquer mon avancement.
Je vous ai envoyé un message privé.
Merci Krom pour ces encouragements !
Ça va vraiment pas être simple de ne pas gérer la partie arrière... Parce que même si c'est simple à faire avec une membrane plane, si je prends une membrane conique, c'est déjà plus compliqué.
Mais je vais bien trouver une solution...
Je continuerais de poster pour expliquer mon avancement.
Je vous ai envoyé un message privé.
Merci Krom pour ces encouragements !
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
37 Posté le 15/05/2016 à 21:02:50
Il faut associer un vecteur "surface" pour chaque source ponctuelle pour l'orienter puis avec le signe du produit scalaire entre le chemin de l'onde et le vecteur tu sauras si tu te trouves devant ou derrière.
Dès que l'on se trouve derrière il faut annuler l'amplitude : On a l'enceinte parfaite.
Dès que l'on se trouve derrière il faut annuler l'amplitude : On a l'enceinte parfaite.
0
EraTom
2282
AFicionado·a
Membre depuis 15 ans
38 Posté le 16/05/2016 à 11:08:40
Citation :
la constante multiplicative et la constante liée à la phase.
Pour la phase, j'ai fait l’hypothèse que tous les points de la membrane bougent en même temps, donc j'ai mis cette constante à 0 pour chaque source.
Pour la constante multiplicative, je me suis rendu compte que, lorsque je passe au calcul du niveau sonore, cette constante multiplicative se transforme simplement en une constante additive, qui ne m’intéresse pas, dans la mesure où je m’intéresse plus aux variations du niveau sonore, qu'à des valeurs en tant que telles.
En effet, le niveau relatif suffit pour faire les calculs. Tu peux faire un bilan de puissance pour appliquer un gain nécessaire a posteriori si tu veux coller à des mesures.
Pour la phase initiale, prendre la même phase pour chaque source ponctuelle revient à dire que la membrane est rigide.
En monochromatique la valeur de la phase initiale importe peu car ça ne change rien car aux zones d'interférence.
Ça peut être plus embêtant si tu souhaites étudier ou mettre en avant les phénomènes de dispersion (retard de groupe, etc.).
Toujours sur le pdf que je t'ai communiqué, tu as la fonction de transfert entre le signal électrique et le rayonnement de la membrane ; en dessous de 400Hz on trouve un filtre passe-haut du 2nd ordre dans le cas de l'enceinte close et tu peux initialiser la phase en suivant la réponse en phase du filtre.
0
- < Liste des sujets
- Charte
- 1
- 2
