Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
Notifications
< Retour vers Théorie musicale
Agrandir
Théorie musicale
Forums thématiques
Théorie musicale
Actu 115 115
Articles 139 139
Médias 1 875 1,9k
Tutoriels
Forums 2 727 2,7k

Sujet frequence fondamentale

  • 14 réponses
  • 9 participants
  • 4 648 vues
  • 5 followers
Sujet de la discussion frequence fondamentale
salut a tous les membres de audio fanzine j veux comprendre qu'est c que ca veut dire une frequence fondamentale et ces quois les harmoniques de la frequence fondamentale
2
Tu taperais "fondamentale" dans Wikipédia, tu trouverais :

https://fr.wikipedia.org/wiki/Fondamentale

Citation :
Harmonie [modifier]

En harmonie, la fondamentale est la note réelle sur laquelle est fondée la « superposition de tierces » d'un accord, et qui donne son nom à celui-ci.

Par exemple, dans l’accord parfait de « do majeur » (do-mi-sol), la note do est la fondamentale. Lorsque l'accord est à l'état fondamental, la fondamentale est à la basse. Au contraire, lorsque l'accord est à l'état de renversement, la fondamentale n'est pas à la basse.

Acoustique [modifier]

En acoustique, la fondamentale peut indiquer la fréquence fondamentale, premier harmonique qui forme la base d'un son musical, et dont la fréquence correspond à la note produite.

 


Cliquer sur les liens permet d'en savoir plus.

Si quelque chose n'est pas clair, on t'explique.

 

[PS] : un petit effort de français et un petit merci à la fin de ton message ne seraient pas de trop. Mais bon...

Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer

[ Dernière édition du message le 28/12/2009 à 10:57:06 ]

3
De même qu'un vecteur peut être exprimé comme une somme de composantes selon les vecteurs unité de chaque axe, eh bien un son peut s'exprimer comme somme de vibrations simples (sinusoïdes), dont les fréquences sont les multiples successifs d'une même fréquence.
[il s'agit évidemment d'un modèle mathématique, je passe sur les conditions indispensables pour que cela soit correct et calculable]

Les axes de coordonnées portent des vecteurs unité "linéairement indépendants" - en pratique orthogonaux.
Les vibrations siimples sont elles aussi indépendantes, ce qui assure l'unicité de la décomposition.
On peut montrer que ces fonctions constituent un espace vectoriel (de dimension entière infinie).

Le poids (coefficient) devant chaque vecteur ou sinusoïde est le produit scalaire du vecteur ou du son avec le vecteur unité ou avec la vibration élémentaire.
La réalisation concrète du produit scalaire dans l'espace des fonctions de vibrations est une intégrale qui s'appelle transformée de Fourier.

Donc (je simplifie) on a quelque chose du genre a*sin(f) + b*sin(2f) +... et la transformée de Fourier consiste à calculer a, b, etc.
4
Aïe. Chuis pas sûr que... enfin, on verra bien.

Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer

5

Ben oui, je ne sais pas s'il veut une explication sur
les harmoniques (le mot figurait quand même dans sa question)
ou
fondamentale d'un accord

Ensuite la question est très large ("je veux comprendre" !), donc il peut y avoir pas mal de façons d'aborder le sujet, et voilà, ça c'est la mienne, attendons d'autres présentations.

 

[ Dernière édition du message le 28/12/2009 à 20:50:07 ]

6
Je pense qu'il confond simplement harmonie et harmonique... Là, c'est vrai que ton explication est super hard ! :lol:

Résultats du questionnaire écolo :

https://fr.audiofanzine.com/le-pub-des-gentlemen/forums/t.178899,le-pub-de-l-ecologie,post.10305303.html

7
Ok, essayons plus simple (quoique, dans mon vieux souvenir, l'espace vectoriel se voit en terminale ou première année de fac ?!)

Un son s'exprime comme une somme de fréquences - appelées harmoniques - qui sont multiples d'une même appelée fréquence fondamentale.
Calculer le poids (la proportion) de chaque fréquence s'appelle "décomposer en série de Fourier". Cela s'exprime mathématiquement par une intégrale.
La collection de coefficients ainsi calculés (qu'on peut représenter sur un graphique) s'appelle le "spectre" du son de départ.

Les fréquences figurant dans la somme sont "pures" (mathématiquement des fonctions du genre sinus).
Quand un son est lui-même presque pur, eh bien la proportion de sa fréquence fondamentale est beaucoup plus importante que celle des autres fréquences harmoniques. Autrement dit, le spectre est constitué d'une grande barre verticale à l'abcisse f, et de toutes petites barres pour les autres fréquences 2f, 3f, etc.
A la limite, pour un son tout à fait pur, il n'y a plus que la fréquence fondamentale f (de même, me revoilà avec mon idée, un vecteur unité sur un axe de coordonnées n'a qu'une seule composante non nulle, à savoir celle sur l'axe qui le porte).

L'unicité de la décomposition en harmoniques n'est pas un détail, cela n'aurait pas d'intérêt de calculer un spectre s'il y en avait plusieurs calculables pour un même son !
Les fonctions sinus avec les fréquences 2f, 3f, etc, sont indépendantes, c'est à dire aucune d'elle ne peut être exprimée comme somme de ses copines (quels que soient les coefficients).
Ce n'est pas évident à montrer.
Par contre, une fois cela admis, cela implique l'unicité de façon triviale :
soit une fonction F admettant 2 décompositions :
F = a*f1 + b*f2 + etc
F = a'*f1 + b'*f2 + etc
Dans ce cas nous avons (a-a')*f1 + (b-b')f2 + etc = 0
ce qui impliquerait par exemple que (a-a')*f1 = (a'-a)*f2 ° + etc
c'est à dire la fréquence pure f1 s'exprimerait comme somme des autres copines pures,
ce qui était exclu par hypothèse.
Donc il ne peut y avoir 2 décompositions sur une collection de fonctions indépendantes, CQFD.

(c'est très différent de la collection de pièces de monnaie dans mon porte-monnaie : là on peut payer une même somme de plusieurs façons différentes, et c'est fait exprès pour maximiser les chances d'y arriver !)

Que dire d'autre, je ne sais pas...

[ Dernière édition du message le 31/12/2009 à 20:09:32 ]

8
Citation :
Ok, essayons plus simple (quoique, dans mon vieux souvenir, l'espace vectoriel se voit en terminale ou première année de fac ?!)
Oh là, ça date ! Un étudiant d'aujourd'hui ne découvre (souvent avec horreur) l'algèbre linéaire (et les autres structures) qu'en première année d'enseignement supérieur, et c'est assez souvent indigeste (même en "math sup") ...

Je pense qu'il vaudrait mieux prendre un exemple simple, comme une corde vibrante (aux extrémités fixées à deux points fixes), et faire les dessins des premier modes propres ?

Wikipédia a justement une animation :

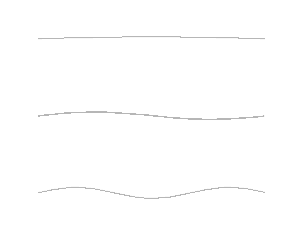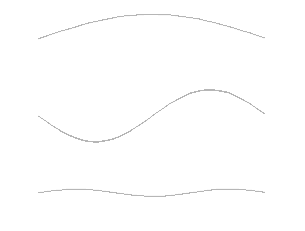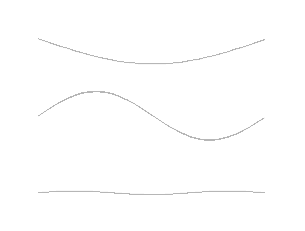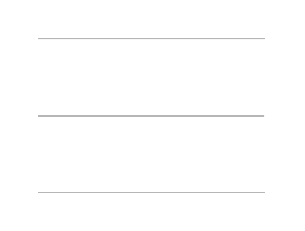
Before you play, ask yourself: will it improve upon the silence ?

9
Moi aussi !

http://www.footballistique.com/forum-foot/images/smilesr/puce.gif

http://r33b.net/

10
lynch_kubrick,

bienvenue parmi nous.

Si après les explications algébriques d'Alain ou l'animation de Fonzy, ça ne va toujours pas, voici une petite page sympa, avec de chouettes graphiques et des explications claires : Fréquence fondamentale et harmoniques
C'est dédié radio amateur, mais le premier exemple est musical. 

Je précise , à tout hasard  que Google est ton ami à toi aussi.  

Jay F.

We're born naked, wet and hungry. Then things get worse.
http://soundcloud.com/jay-f-2