Aujourd’hui, nous étudierons un autre élément central de la synthèse sonore, j’ai nommé les filtres.
Ceux-ci sont abondamment employés en synthèse soustractive, elle-même la plus répandue des formes de synthèse, ce qui fait que l’on retrouve les filtres sur un grand nombre d’appareils réels ou virtuels. Nous reviendrons sur la synthèse soustractive plus en détail ultérieurement. Mais sachez que le principe est de sculpter le son en partant d’une source sonore riche en harmoniques que l’on peut retirer ou bien accentuer… grâce aux filtres, justement !
Ceux-ci sont de plusieurs types, en fonction que l’on souhaite couper ou accentuer telle ou telle plage de fréquences : filtres passe-bas, passe-haut, passe-bande et coupe-bande. Mais avant de voir ce qui les différencie, considérons d’abord ce qui les rassemble.
Caractéristiques communes
Tous les filtres fonctionnent par la combinaison d’une ou plusieurs « fréquences de coupure » et d’une « pente ». Une fréquence de coupure est une fréquence, définie par l’utilisateur du filtre, la plupart du temps grâce à un potentiomètre. C’est à partir de cette fréquence – ou avant celle-ci, selon le filtre – que les autres fréquences vont être coupées, même si « atténuées » serait plus exact.
La pente du filtre définit la rigueur avec laquelle le processus va avoir lieu. L’atténuation en question est exprimée en décibels/octave. Plus le nombre de décibels est élevé, plus l’atténuation est drastique. Ainsi, un filtre ayant une pente de 12dB/octave appliquera une atténuation deux fois supérieure à celle produite par un filtre ayant une pente de 6dB/octave.
Vous verrez souvent, sur les synthés, une indication d’un nombre de « pôles » : filtre « 2 pôles », « 3 pôles », etc. Il s’agit en fait d’une manière de définir la pente du filtre concerné, par paliers de 6dB/octave. Ainsi un filtre « 2 pôles » désigne un filtre ayant une pente de 12dB/octave, « 3 pôles » un filtre ayant une pente de 18 dB/octave, et ainsi de suite. La référence en matière de filtres reste le filtre Moog « 4 pôles », soit 24dB/octave, qui est l’un des plus rigoureux et les plus « typiques » du marché.
À noter que la fréquence de coupure peut être accentuée par un paramètre quasiment toujours présent pour les filtres : la résonance (voir exemple dans le paragraphe « Filtre passe-bas »).
Les points communs à présent clarifiés, nous pouvons maintenant nous pencher sur les différents types de filtres.
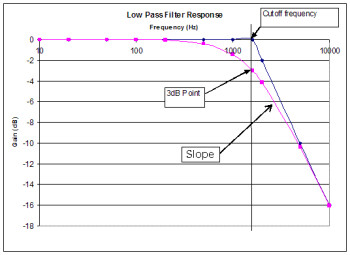
Filtre passe-bas (en anglais : low-pass filter)
C’est le type de filtres le plus usité en synthèse, à tel point que certains appareils ne proposent parfois que ce type de filtrage. Il est destiné à ne laisser intactes que les fréquences situées en dessous de sa fréquence de coupure, et à atténuer toutes celles situées au-dessus. Il est parfois également appelé « filtre coupe-haut ».
Ici un exemple sonore avec un signal affecté par un filtre passe-bas dont on déplace la fréquence de coupure de plus en plus vers les basses, puis à nouveau vers les aigus :
Puis, le même exemple avec l’effet de résonance :
Filtre passe-haut (en anglais : high-pass filter)
C’est l’inverse du précédent. Le filtre passe-haut est destiné à ne laisser intactes que les fréquences situées au-dessus de la fréquence de coupure, et à atténuer celles situées au-dessous. Il est parfois également appelé « filtre coupe-bas ».
Ici un exemple sonore avec un signal affecté par un filtre passe-haut dont on déplace la fréquence de coupure de plus en plus vers les aigus, puis de nouveau vers les basses :

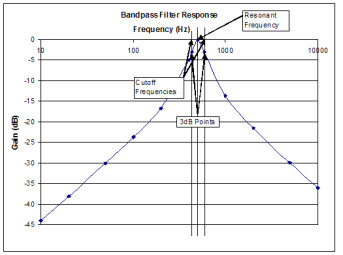
Filtre passe-bande (en anglais : band-pass filter)
Ce filtre est destiné à ne laisser passer qu’une certaine plage de fréquences, située entre deux limites. Différemment des deux filtres précédents, celui-ci dispose donc de deux fréquences de coupure, une inférieure et une supérieure. Ce filtre est donc la combinaison d’un passe-haut et d’un passe-bas.
À noter que c’est ce type de filtres qui est utilisé en radio et en télévision pour permettre de passer d’une station ou d’une chaîne à l’autre, en isolant à chaque fois la plage de fréquences de diffusion (ne pas confondre avec les fréquences audio) de chacune d’elle.
Ici un exemple sonore avec un signal affecté par un filtre passe-bande dont on déplace les fréquences de coupure de plus en plus vers les aigus, puis à nouveau vers les basses :

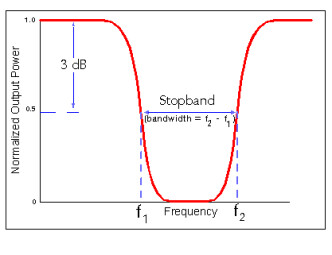
Filtre coupe-bande (en anglais : notch filter)
Ce dernier type de filtres est le contraire du précédent : il définit une plage de fréquences qui doit être atténuée entre deux limites. Lui aussi dispose donc de deux fréquences de coupure, et combine donc également un passe-haut et un passe-bas.
Ici un exemple sonore avec un signal affecté par un filtre coupe-bande dont on déplace les fréquences de coupure de plus en plus vers les aigus, puis de nouveau vers les basses.