Sujet Comparaison de synthèses : modulation de phase et modulation de fréquence

Dans ce cas particulier, la fréquence de répétition (la plus basse) est celle de la porteuse. Ce n'est pas vrai dans le cas général.

EDIT : pour virer la porteuse de ce signal, il suffit de prendre m=2.4048.

Salut a tous

Concernant la définition mathématique de la FM et la PM, c'est un peu plus compliqué pour la FM

Modulation de fréquence (laissez beton la seconde égalité):

 

où f(tau) est la fréquence instantanée, fp est la fréquence porteuse, fdelta est l'index de modulation et

xm(tau) le signal modulant

 Pourquoi cette expression aussi complexe ? En fait on concoit assez bien qu'une modulation de fréquence fait varier la fréquence instantanée du signal, f(t)...Cette frequence instantanée est définit comme étant la dérivée de la phase instantanée.

Pulsation instantanée :

Soit O(t) la phase instantanée d'un signal x(t)=sin(O(t)). La pulsation instantanée (w(t)=2.pi.f(t) ou f(t) est la fréquence instantanée) est égale à w(t)=2.pi.f(t)=dO(t)/d(t).

Dans l'equation barbare de la modulation de fréquence, si vous prenez O(t)=2.pi.int_{0}^{t}f(tau)dtau et que vous dérivée tout ca, vous allez trouvez que la pulsation instantanée est égale à 2.pi.f(t) et que donc la fréquence instantanée est égale à f(t).

Exemple d' Equivalence FM-PM :

 

Si on prend un signal modulé en phase avec une modulante en cosinus du type

 

x(t)=sin(O(t))=sin(2.pi.fp.t+cos(2.pi.fm.t)), où la phase instantanée est égale à O(t)=2.pi.fp.t+cos(2.pi.fm.t) ou fp est la fréquence porteuse, fm est la fréquence modulante

 

Si je veux calculer la fréquence instantanée, je dérive simplement O(t) et j'obtiens alors la pulsation instantanée:

 

w(t)=dO(t)/dt=2.pi.fp+2.pi.fm.sin(2.pi.fm.t)

 

et donc comme la fréquence instantanée et la pulsation instantanée sont reliées par l'equation w(t)=2.pi.f(t), on trouve alors:

 

f(t)=fp+fm.sin(2.pi.fm.t)

 

soit une modulation de fréquence avec un index de modulation égal à fm et un signal modulant égal à sin(2.pi.fm.t).

 

Concernant le spectre d'un signal FM, la formule precedement citée donne une bonne partie de la réponse:

Si on vous demande de calculer le spectre, via la transformée de Fourier, ne vous amusez pas a la calculer a partir de la premiere égalité...essayez plutot avec la seconde egalité c'est nettement plus simple. En invoquant la propriété de linearité de la transformée de Fourier et la transformée de fourier d'un cosinus, on calcule ca simplement...on voit notamment que le signal se compose d'une infinité de pic fréquentiel (voila le plus gros interet de la FM et de la PM au niveau sonore) placés aux fréquences fp+n.fm....(n etant un entier)

En régle générale, le signal n'est pas harmonique car ces pics ne sont pas multiples de fp. Toutefois lorsque fm est un multiple de fp, alors la le signal est harmonique, ce qui est tres interessant au niveau sonore...

++

Citation de Choc :

En régle générale, le signal n'est pas harmonique car ces pics ne sont pas multiple de fp. Toutefois lorsque fm est un multiple de fp, alors la le signal est harmonique,

C'est bien ce que je disais, mais sous une autre formulation ! 

se placer dans un cadre non-harmonique et faire appel à la transformée de Fourier, c'est un peu difficile, d'où l'hypothèse déjà évoquée plus haut de se restreindre aux signaux périodiques.

si j'ai bien compris:

la phase instantanée est l'ensemble de ce qu'il y a dans le sinus (ou cosinus).

la pulsation instantanée est la dérivée de la phase instantanée et inversement la phase instantanée est l'intégrale dans le temps de la pulsation instantanée...

donc après ce n'est plus qu'une question de dérivation/intégration d'une sinusoide à une fréquence donnée qui donne une autre sinusoide à la même fréquence... grossièrement

remarque: la fréquence instantanée d'un signal semble pouvoir être retrouvée par la transformée de Hilbert-Huang. Sinon, le FM8 fonctionne comment alors  ?

Pour info, il semble y avoir des articles intéressants, théoriques et pratiques à partir de ce lien : https://en.wikipedia.org/wiki/Frequency_modulation_synthesis  

DrPouet > Ca date

 

Citation de lulumusique :

donc après ce n'est plus qu'une question de dérivation/intégration d'une sinusoide à une fréquence donnée qui donne une autre sinusoide à la même fréquence... grossièrement

Yep c'est ca ! 

Citation de pluton 35 :

se placer dans un cadre non-harmonique et faire appel à la transformée de Fourier, c'est un peu difficile, d'où l'hypothèse déjà évoquée plus haut de se restreindre aux signaux périodiques.

 Dans le cas d'une sinusoide modulé en phase (ou fréquence) par une sinusoide c'est pas trop compliqué...en fait vu l'equation:

on trouve directement la transformée de fourier...celle ci est egale à:

X(f)=sum_{n=-infty}^{infty}A.J_n(beta).(delta(f-(fp+nfm))+delta(f+(fp+nfm))

donc une infinité de pics, placés aux fréquences fp+nfm (n entier) et dont l'amplitude est donnée par le coefficient de bessel Jn(beta)...un simple changement de l'index de modulation beta peut avoir une repercution importante sur les amplitudes des composantes fréquentielles.

Citation de pluton35 :

remarque: la fréquence instantanée d'un signal semble pouvoir être retrouvée par la transformée de Hilbert-Huang

 En régle general oui, mais dans certains cas c'est comme utiliser une ferrari dans une route limitée a 30km/h.

• Si x(t)=sin(O(t)), alors O(t) peut etre retrouvé simplement (avec des ambiguités potentielles) via la fonction arcsin..c-a-d O(t)=arcsin(x(t))
• Si x(t)=a(t)sin(O(t)), c-a-d un signal monocomposante modulé en phase et en amplitude, on peut utiliser la transformée de Hilbert ou alors l'operateur d'énergie de Teager...
• Si x(t)=sum_{n}a_{n}(t)sin(O_{n}(t)), c-a-d un signal mutlicomposante la decomposition modale empirique (EMD) permet de séparer les différents élements de la somme...ensuite on revient dans le cas precedant et on peut utiliser soit Hilbert soit Teager...On donne également le nome de transformée de Hilbert/Huang ou Teager/Huang pour cette approche.

Citation de pluton35 :

Sinon, le FM8 fonctionne comment alors  ?

 Dans les synthé, il n'est pas necessaire d'estimer la fréquence instantanée ou la phase instantanée...EN fait, dans le FM8, le coeur du moteur de synthèse c'est la matrice placée à droite..

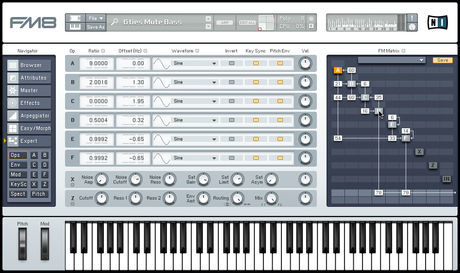
Le FM8 possede plusieurs oscillateurs...(A,B,C,D etc). A chaque oscillateur on spécifie une forme d'onde (sinusoide, mais pas seulement), une fréquence fondamentale (par rapport à la note jouée). Ensuite la matrice permet de specifier qui module qui. Le nombre specifié entre le modulateur et le modulant correspond à l'index de modulation. On concoit assez bien que, même si dans des cas simples le signal de sortie peut se calculer facilement, dans le cas général c'est beaucoup plus compliqué !

Dans le FM8, il y a une previsualisation de la forme d'onde et du spectre de sortie. A mon avis, tout cela est calculé à partir d'une rapide simulation !

merci pour ces détails. La série série impliquant les fonctions de Bessel ressemble, je crois, à une double série de Fourier en m*fp+n*fm pour les signaux apériodiques, composés de deux fréquences sans dénominateur commun, mais limitée à m=1. On obtient alors la série de Fourier simple d'un signal xp(t), qui peut ne pas être périodique du fait de la présence de fp. C'est un cas assez particulier j'ai l'impression : je me trompe ?