réactions au dossier [Bien débuter] Anatomie des ondes
- 113 réponses
- 26 participants
- 15 599 vues
- 28 followers
Afficher le sujet de la discussion
Anonyme
261
trazom
1819
AFicionado·a
Membre depuis 20 ans
Anonyme
970
Hors sujet :
Citation de KaeRZed :Tchandra, tu as le droit de poser toutes les questions que tu souhaites.... Dès l'instant qu'elles sont posées dans une discussion en rapport
Pas de soucis, mais la discussion était basée sur cette citation de l'article :
Citation :Pour information, on doit au génial mathématicien et physicien Joseph Fourier (1768-1830) la découverte suivante : toute onde complexe peut être décomposée en un certain nombre d’ondes sinusoïdales simples, à l’exception des transitoires, qui sont les périodes d’établissement et de disparition du son.
Après, la discussion a émergée d'elle-même à cause des intervenants qui avaient quelque chose à dire à ce sujet, je n'aurais pas pensé à poser cette question sinon, et ouais ça me saoule que d'avoir à se censurer dès qu'on dit des trucs un peu compliqué, quand des gens racontent n'importe quoi sur le forum, je ne vais pas leur dire d'aller ailleurs parce qu'ici c'est un forum d'audio et non le café du coin, je zappe la discussion et voilà...
Citation :En plus j'ai écouté les compos de Tchandra et je dis : bravo.
Merci, c'est sympa
Citation :Oui pourquoi pas.Pour ne pas donner la nausée aux gens on peut demander à un modo de déplacer notre échange dans un fil spécifique, non ?
Citation :Je vois l'idée, merciCa marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).
sleepless
2192
Rédacteur·trice
Membre depuis 19 ans
miles1981
8360
Je poste, donc je suis
Membre depuis 20 ans
sleepless
2192
Rédacteur·trice
Membre depuis 19 ans
EraTom
2282
AFicionado·a
Membre depuis 13 ans
Bon ok, alors j'y vais franco et le post sera déplacer si besoin...
Dans le cas de continu, on calcule une densité de puissance qui permet de retrouver la puissance dans une bande de fréquence en calculant une intégrale.
Franchement, ça va loin et les physiciens ne s'embarrassent généralement de ce genre de "détail".
Si tu veux un parallèle, c'est comme la définition de densité de probabilité continue qui permet de calculer la probabilité que la valeur prise par une variable aléatoire soit dans un intervalle donné.
https://fr.wikipedia.org/wiki/Densit%C3%A9_de_probabilit%C3%A9
Comme expliqué dans cette article, dans le cas continu la probabilité que la variable aléatoire prenne une valeur donnée est nulle : P( X = x ) = 0 ≠ f(x)
Mais la densité permet de calculer P( a < X < b ) = ∫ f(x).dx pour x sur
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...
[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.
Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.
Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
Pas contre si X est une variable discrète P( X = x ) ≠ 0 et P( a < X < b ) = ∑ P( X = x ) pour x dans https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.
Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.
Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade.
Citation :
La projection sur une base c'est valable dans le cas discret et la série de Fourier : C'est la projection sur une base d'un espace (vectoriel) pré-hilbertien.Par contre, c'est curieux cette histoire de puissance dont tu parles. Ce que j'avais retenu, c'est que transformée de Fourier est une projection d'une fonction sur une base de type exp(2Pi.f.t) avec f réel (alors qu'il s'agit de nombres entiers pour la décomposition en série) et que ça s'appliquait à tout signal... donc pour moi le spectre, ça indique simplement l'amplitude de telle ou telle composante (haute fréquence, basse fréquence etc) pas la puissance...en général quand on calcule une puissance ou une énergie, on utilise le carré du signal à un moment donné, mais bon si tu dis que le spectre donne une idée de la puissance du signal en fonction de la bande de fréquence, je te crois mais je ne pige pas d'où ça vient...
Dans le cas de continu, on calcule une densité de puissance qui permet de retrouver la puissance dans une bande de fréquence en calculant une intégrale.
Franchement, ça va loin et les physiciens ne s'embarrassent généralement de ce genre de "détail".
Si tu veux un parallèle, c'est comme la définition de densité de probabilité continue qui permet de calculer la probabilité que la valeur prise par une variable aléatoire soit dans un intervalle donné.
https://fr.wikipedia.org/wiki/Densit%C3%A9_de_probabilit%C3%A9
Comme expliqué dans cette article, dans le cas continu la probabilité que la variable aléatoire prenne une valeur donnée est nulle : P( X = x ) = 0 ≠ f(x)
Mais la densité permet de calculer P( a < X < b ) = ∫ f(x).dx pour x sur
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...
[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...
[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
Pas contre si X est une variable discrète P( X = x ) ≠ 0 et P( a < X < b ) = ∑ P( X = x ) pour x dans https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...
[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade." rel="ugc noopener" target="_blank">
En toute rigueur tu te retrouves dans le même cas pour la puissance dans le domaine fréquentiel ; c'est ce que le terme "densité" signifie. Et comme l'indique la suite de l'article Wikipédia, les physiciens utilisent une définition qui n'est pas complètement rigoureuse et qui peut ne pas fonctionner pour certaines classes de signaux.
Dans le cas continu, dire que la densité de puissance en "f" correspond à la puissance d'une sinusoïde à cette fréquence est abusif.
Dans le cas discret (ce que tu obtiens avec une FFT) tu peux "confondre" la densité et la puissance à une fréquence données sans vergogne.
[quote]Mais j'imagine que tu décris une méthode d'analyse qui utilise une sorte d'effet de moyenne, on fait plusieurs fois le même calcul sur une "trame" et on détermine le spectre final en "moyennant" les différents spectres obtenus. Je comprends bien que ce n'est pas applicable avec un signal qui n'est jamais identique, mais il s'agit là d'une méthode pour améliorer la précision de la transformé de Fourier, je ne vois pas en quoi ça empêche de faire la transformée de Fourier d'un transitoire unique et en quoi le spectre obtenu serait inutilisable...[/quote]Ce n'est pas seulement pour améliorer la précision mais bien pour parvenir à l'estimation.
Dans le cas le plus général, le signal n'est pas déterministe mais aléatoire. C'est un processus stochastique (bon courage... https://fr.wikipedia.org/wiki/Processus_stochastique )
En gros, le signal est la réalisation d'un truc aléatoire (comme un jeté de dé) et pour calculer la densité de puissance il faut calculer l'espérance mathématique (la moyenne en probabilité) du carré de la transformée de Fourier du processus stochastique qui forme le signal. Dans la littérature tu pourras rencontrer la formule DSE = E[|S(f)|²].
Or obtenir les différentes réalisations du signal n'est pas possible dans la pratique ; l'idée est alors de faire une moyenne temporelle mais ce n'est possible que si le processus possède deux propriétés : stationnaire et ergodique.
https://fr.wikipedia.org/wiki/Processus_stationnaire
https://fr.wikipedia.org/wiki/Processus_ergodique
Dans le cas de signaux musicaux ceci n'est pas toujours vérifié notamment sur les sons de percussions ou les transitoires trop rapides : L'estimation du spectre est alors biaisée.
Pour caractériser un bruit (un processus stochastique)... Même avec le calcul d'un FFT (discrète), le décrire comme une somme de sinusoïdes (amplitude, fréquence, phase) n'est vraiment pas pertinent : Donner l'enveloppe de la puissance suffit sachant, qu'en plus, il n'y a pas de phase particulière à retenir (c'est quoi la phase d'un bruit sinon un artefact de calcul valable pour une seule estimation du spectre ?).
[quote]Bon, comme je disais plus haut, le fait que le signal mesuré soit de durée fini et qu'on le projette sur une base de fonctions infinies, ça donne des résultats bizarres comme les sinus cardinaux etc, mais je ne vois en quoi le problème serait pire pour un transitoire que pour un autre type de signal...
[/quote]Le problème d'un transitoire (rapide) qui s'ajoute est que la transformée de Fourier trouve une limite en résolution : Tu ne peux pas distinguer les "raies" dans le domaine fréquentiel si la durée du signal (ou de l'évènement sonore que tu tentes de caractériser) est trop court.Il faut alors passer à d'autres techniques dites Haute Résolution. En général les techniques proposent d'introduire de la connaissance a priori : Par exemple, on "sait" que le signal est une somme de sinusoïdes, des sinusoïdes amorties ou des atomes de Gabor (les ondelettes) et l'on cherche à estimer les paramètres qui permettent de coller au mieux à la trame du signal dont l'on dispose.
L’intérêt pour le traitement du signal musical est bien réel mais le coût calculatoire est prohibitif. Ça fait plus d'une dizaine d'années que des labos planchent activement sur des algo pour réduire le coût calculatoire (la puissance de calcul de nos machines augmentant dans le même temps).
Les candidats pour la prochaine génération d'encodeur audio proposent ces techniques notamment pour améliorer la représentation et la reproduction des transitoires rapides.
Les méthodes MUSIC et ESPRIT du lien de Choc sont des méthodes HR.
Edit : Une thèse de Télécom ParisTech qui raconte la même chose et qui propose des algo https://tel.archives-ouvertes.fr/tel-00009321
J'avais bossé à distance avec un certain Rémi Boyer qui menait une thèse sur le sujet à Télécom ParisTech qui allait jusqu'à proposer un encodeur audio mais elle ne semble plus en ligne... Peut-être en cherchant un peu...
[quote]Par exemple, il est bien possible de filtrer un transitoire, si on lui applique un passe-bas, on va le "lisser" , c'est-à-dire réduire ses composantes hautes fréquences, j'en déduis que ces fréquences sont bien là non ? Bon certes, on va aussi ajouter des composantes qui viennent du filtre lui-même (résonance, déphasage, etc) mais c'est autre chose...[/quote]En réalité c'est une autre façon de voir la FFT et tu vas rencontrer les mêmes limitations.
[quote]Pour le principe d'incertitude d'Heisenberg, je ne savais pas qu'il s'appliquait ici, je pensais que c'était un truc réservé à la mécanique quantique...[/quote]Ben en fait ça s'applique à chaque espace dual... Et c'est bien le même problème (c'est une fonction d'onde qui régit la mécanique quantique) : Position <-> Quantité de mouvement d'une particule
Localisation temporelle d'un signal <-> Localisation fréquentielle
[quote]Merci pour tes conseils concernant le réglage des analyseurs de spectre, mais concrètement, ça ne m'aide pas beaucoup parce que si tu utilises un analyseur de spectre du commerce dans ton daw, généralement, tu ne peux pas régler le type de fenêtrage, la durée des trames oui, mais dans un signal d'un morceau de musique, il y a des transitoires partout (le début de chaque note...), donc concrètement si tu appliques un EQ sur un son percussif, et que tu regardes le spectre du signal filtré pour mieux voir ce qui passe au niveau des fréquences, est-ce que ça veut dire 80% de ce que tu vas lire dans ton spectre ne sera que du "bruit" de fenêtrage ? Est-ce que les analyseurs de spectre pour l'audio (je en sais pas, les trucs utilisés en mastering etc) ne sont pas optimisés pour afficher un résultat exploitable ? Peut-être qu'ils utilisent d'autres algo que la transformée de Fourier, ondelettes ou les "méthodes paramétriques" (connais pas...) ?[/quote]Oui les outils d'une DAW sont assez souvent limités en terme de réglages... Alors autant avoir conscience des limites.
Le spectre d'un signal proche de l'impulsion sera complètement étalé dans les fréquences et pourra avoir la même tête qu'un bruit (qui lui est réellement présent partout). Ça se complique encore si le son en question est un bruit modulé rapidement en amplitude (genre une caisse claire ou un coup de charleston).
Mon avis et mon expérience (que tout le monde ne partage sans doute pas) sont que dans ces cas là il vaut mieux faire confiance à ses oreilles qu'à ce qu'on lit sur un analyseur parce qu'il ne te donnera qu'une idée grossière de ce qu'il se passe réellement.
[quote]Ca marche très bien, c'est juste que tu considère le transitoire comme étant périodique (période = durée de ton signal original).[/quote]Ok pour la méthode, mais malheureusement ça ne marche pas toujours très bien : Tout dépend de la durée du phénomène et de la résolution fréquentielle dont on a besoin... On va dire que dans 90% des applications audios ça suffit.
[quote]Par contre, je relativiserai un peu certains discours. [/quote]Nan !
Bon ok, mais moi je suis signaleur ET batteur alors la représentation spectrale des percussions ça me chatouille. Ce qu'en fait le mp3 ça me rend même parfois malade.
[ Dernière édition du message le 23/09/2014 à 00:52:36 ]
Danguit
3348
Squatteur·euse d’AF
Membre depuis 18 ans
miles1981
8360
Je poste, donc je suis
Membre depuis 20 ans
Choc
6968
Membre d’honneur
Membre depuis 22 ans
L'appareil auditif est très complexe.
Les courbes de Fletcher Munson te permettent d'établir un lien "approximatif" entre l'amplitude d'une composante et l'intensité perçue.
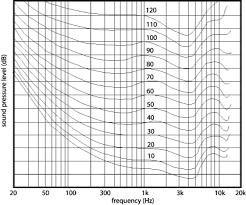
Les courbes de Fletcher Munson te permettent d'établir un lien "approximatif" entre l'amplitude d'une composante et l'intensité perçue.
Site personnel: https://www.enib.fr/~choqueuse/
[ Dernière édition du message le 23/09/2014 à 09:31:59 ]
- < Liste des sujets
- Charte