[Théorie] Repliement spectral : c'est quoi ? ça s'entend ?
- 33 réponses
- 10 participants
- 12 700 vues
- 21 followers
Dr Pouet
Citation : Bon, sinon, le repliement quand on échantillonne à 44.1kHz, ça s'entend ? V'z'avez un exemple concret de deux fichiers 44.1 / 96 sur lequel la différence s'entend ?
Désolé, je passe surement pour un benet, mais moi j'ai jamais entendu la différence, et théoriquement on a vu que si le filtrage était correct (ce qui doit être le cas quasi tout le temps à partir d'un certain niveau de matos heureusement de plus en plus bas) ça s'entend pas.
- 1
- 2
Dr Pouet
Citation : Typiquement, on peut faire un signal carré parfait à 1000 Hz sur Matlab (avec juste des 1 et des -1), l'échantillonner en 44.1 kHz et en 96 kHz, là à mon avis la différence est flagrante, surtout si on augmente de plus en plus la fréquence du signal.
Maintenant, en pratique, tous les traitements numériques de base gèrent ça... plus ou moins bien (voir par exemple un sujet que Choc a posté sur l'aliasing où il compare l'efficacité des filtres anti-repliements de plusieurs synthés, en particulier Reaktor qui est naze à ce niveau là et Synthedit qui filtre de manière trop violente).
/techniques-du-son/forums/t.197376,choky-lab-l-aliasing-c-est-quoi-donc-demos-sur-modulaires.html
D'où l'intérêt premier de travailler à fréquence d'échantillonnage élevée, pour compenser ces imperfections.
Citation : Un signal avec des 1 et des 0 ne peut pas etr eun signal carre parfait, puisque tu peux peux pas avoir de pente infinie. Et un signal a 1000 Hz, s'il est carre, il a un spectre a support infini en theorie...
Quand on parle de synthese, en particulier de signaux de base, les problemes d'enchatillonage sont assez complexes. Car a part la sinusoide, ils ont tous en theorie des spectres infinis (triangle, carre et pwm, dent de scie); generer le signal de maniere naive donne le pire resultat possible (ie sampler le signal theorique).
T'as la methode BLIT: https://www.music.mcgill.ca/~gary/307/week9/bandlimited.html
Mais il y en a d'autres.
Mais le probleme est different: il s'agit ici d'approcher un signal a spectre infini dans le domaine numerique, et non de sampler un signal a spectres etendu.
Citation : > Le repliement quand on échantillonne à 44.1kHz, ça s'entend ?
Ben non, parce que le signal a été filtré avant. Si ce n'est pas filtré, alors oui, ça s'entend. Mais on filtre systématiquement.
Simplement, avec du 44 on filtre à environ 20kHz, alors qu'avec du 96kHz on peut filtrer théoriquement à 48kHz.
Citation : Gabou > Je comprends pas ce que tu veux dire alors ? Un signal carre a 1000 Hz va avoir plus de repliement a 44.1 qu'a 96 khz sans filtre, et ?
Bara parle de "fichiers" sur lesquels il y aurait du repliement qu'on "entendrait" plus à 44.1K qu'à 96K. On peut faire ça avec un signal carré, ou une sinusoide à 26K
> Je serais surpris qu'un convertisseur de bonne qualite laisse passer une sinusoide a 26 khz ? J'ai jamais fait l'experience, remarque.
Wolfen Compos! Détail de la configuration informatique
Ben non il la laissera pas passer, elle va se replier à 18K en 44.1K, d'où la différence entre le fichier échantillonné en 44.1K et celui en 96K ou y'aura pas la même chose en sortie de convertisseur
Après peut-être que le convertisseur 96K filtre en plus tout ce qui n'est pas dans le domaine de l'audible
> Quand je dis passera pas, je parlais du filtre anti repliement. Si vraiment la sinusoide a 26 khz est repliee a 18 avec une amplitude importante, j'aurais tendance a penser que c'est la preuve d'un tres mauvais convertisseur.
Dr Pouet
Supposons que l'on regarde tourner une roue, au début arrêtée, mais qui tourne de + en + vite. On la voit accélérer, puis ralentir, jusqu'à sembler s'arrêter, et se mettre à tourner à l'envers de plus en plus vite.
Le système d'observation (oeil + cerveau) se comporte comme un échantillonneur à une fréquence F donnée, c'est la conversion analogique vers numérique. A partir d'une certaine vitesse (F/2), l'échantillonneur n'est plus capable de rendre compte du phénomène réel. Ce phénomène ressemble terriblement au comportement de la sinusoïde montant à 44kHz dans le thread de Choc sur l'aliasing, et pour cause !
On peut retenir la règle : un fichier audio à 44kHz ne doit pas contenir d'information qui chercherait à retranscrire une sinusoïde de plus de 22kHz.
Si on essaie d'écrire un sinusoïde de 32kHz dans un tel fichier, ça fera une jolie sinusoïde de 10kHz (32-22), donc pas du tout l'effet recherché !
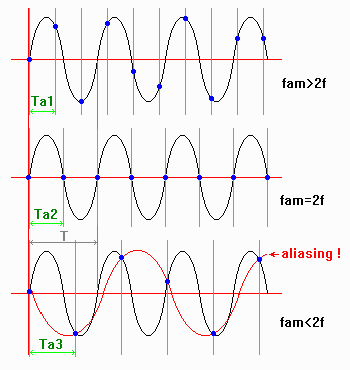
En voici une illustration :

http://paginas.terra.com.br/lazer/py4zbz/teoria/amostr1.gif
Les barres vertes représentent l'instant d'échantillonnage. En bas, les deux sinusoïdes conduisent à exactement la même mesure. La sinusoïde noire effectue une période (T en gris) en un peu moins de 2 traits verts, sa fréquence est effectivement supérieur à la fréquence d'échantillonnage divisée par 2, d'où la confusion. Cette confusion est impossible avec des sinusoïdes de fréquence inférieure à F/2.
En rapport avec la question de Bara :
Pour mettre en évidence des défauts de filtrage ou de repliement dans un convertisseur, on pourrait utiliser la stratégie suivante : générer un fichier qui contient une ou plusieurs sinusoïdes, mais aucune n'ayant une fréquence supérieure à 22kHz. Comme ça, on est sûr que le fichier lui-même ne contient pas de défaut de repliement, et si on en entend, cela viendra forcément du convertisseur.
Mais je ne vois pas très bien quel signal précisément mettre pour repérer facilement ce défaut à l'oreille...

Qu'en pensent les spécialistes du traitement du signal :
- des erreurs dans mon raisonnement ?
- une suggestion pour un signal de test démonstratif ? (au début je pensais à une somme de sinusoïdes s'approchant d'un signal carré, mais il me semble que ça n'a pas de sens : les défauts devraient aussi bien s'entendre sur une sinusoïde pure non ? )
francolamuerte
Dvt

Le spectacle
Number-6
Laminttikia
Dr Pouet, tu as parfaitement compris le principe et ta métaphore de la roue qui semble tourner à l'envers est excellente! C'est le théorème de Shannon ou le critère de Nyquist qui font état de cela.
Le repliement de spectre est un phénomène qui s'observe lors de l'utilisation d'un convertisseur analogique-numérique (ADC). C'est pourquoi avant d'attaquer un ADC on passe par un filtre anti-repliement (ou anti-aliasing) d'ordre très élevé et qui permet d'atténuer drastiquement les fréquences supérieures à fe/2.
Par contre j'ai du mal à comprendre le fait de générer une sinusoide de façon logicielle puisque là tu sors sur un DAC qui, à ma connaissance ne possède pas de filtre anti-repliement mais un filtre de reconstruction (qui n'a rien à voir).
Je ne vois pas quel défaut tu veux mettre en évidence dans le cas présent
Will Zégal
Hors sujet : DP : j'ai modifié ton message pour ajouter l'image en lien. Chez moi, elle n'apparaissait pas ;)
Flag déguisé
francolamuerte
Pour ma part le lien ne fonctionne pas. Ça m'ammène sur un obscur site espagnol.
Hasta Luego !
Laminttikia
Citation : Ça m'ammène sur un obscur site espagnol.
francolamuerte
Esta página está fora do ar Provavelmente, o autor do site ainda não fez a publicação das páginas nos nossos servidores. Tente novamente outra hora.
Traduction Google :
This page is is of air Probably, the author of the site not yet made the publication of the pages in our servers. It tries another hour again.
Et traduction à partir de l'anglais :
Cet IS-IS de page d'air probablement, l'auteur de l'emplacement pas encore fait la publication des pages dans des nos serveurs. Elle essaye une autre heure encore.
C'est le téléphone arabe !
Allez on parle d'Aliasing. Il y a de l'aliasing dans les lignes de téléphone ?
Dr Pouet
http://drpouet.free.fr/images/son/aliasing.gif
Citation : Par contre j'ai du mal à comprendre le fait de générer une sinusoide de façon logicielle puisque là tu sors sur un DAC qui, à ma connaissance ne possède pas de filtre anti-repliement mais un filtre de reconstruction (qui n'a rien à voir).
Je ne vois pas quel défaut tu veux mettre en évidence dans le cas présent
C'est une bonne remarque. Moi non plus je ne vois plus
Au début on a parlé de la conversion NA (ou DAC en inegliche), puis du filtrage assez raide qui le suit et qui pouvait être un problème (phase massacrée...) On a évoqué la solution : suréchantillonnage + filtrage moins raide, et donc avec moins de problèmes de phases.
Et au milieu de ça on a parlé du repliement spectral :
Citation : Apres, il y a les convertisseurs: si on a un signal dont la bande passante max est de 20 khz environ, on peut se dire que ca sert a rien d'avoir un convertisseur qui marche a plus. En fait, le probleme est que si le convertisseur marche a 44.1, il doit filtrer tout ce qui passe au dela de 22.05 (la moitie); tout ce qui sera pas filtre se "retournera" (repliement de spectre, autrement connu sous le nom d'aliasing). Et en meme temps, il doit preserver tout ce qui est au dessous.
Mais faire un filtre qui laisse tout passer avant 22050 Hz et tout apres 22050, c'est impossible; on veut des filtres a pente tres raide (beaucoup plus raide que les filtres utilises dans les effets/synthes, car on veut qqch de l'ordre de 50, 60 dB voire bien plus par octave); pente raide veut dire reponse en phase du filtre completement distordante (comprendre ca va chier sur les transitoires). Comme en plus ce doit etre un filtre analogique, ca complique encore plus le truc.
Maintenant, si tu fonctionnes a 96 Khz, le repliement commence a 48 khz. Si on a du signal a 49 khz, ca va etre replie a 47, a 52 replie a 44, etc... Mais meme un repliement de 10 khz, on s'en fout, car c'est a 10 khz de 48, qu'on entend toujours pas. C'est la l'interet fondamental: on deplace la frequence de coupure, on a un filtre beaucoup plus doux, car pas mal de repliement s'entend pas, alors qu'en 44.1, le moindre repliement s'entend.
Reprenons les choses dans l'ordre :
1- on a un signal numérique (fichier wav, CD...) sans repliement
- En effet, si il comporte du repliement, par exemple à 13kHz, ben c'est trop tard pour s'en débarrasser sans virer des parties utiles du signal.
Pour éviter qu'il y en ait : soit l'échantillonneur ADC a viré les fréquences supérieures comme tu l'as indiqué, soit les algorithmes utilisés pour générer le wav s'en sont chargés, c'est ce que Choc décrit dans son sujet
2- on fait une conversion numérique -> analogique (DAC)
- je ne sais pas à quoi le signal ressemble à ce stade, probablement des histogrammes un peu arrondis. Quelqu'un le sait ça ?
Dans ce cas, en plus du signal utile, on doit avoir des tas d'harmoniques multiples de 44.1kHz ; mais là on est en analogique, donc il n'y a plus de raison d'avoir du repliement
3- on filtre
- Ca a pour effet de virer les harmoniques précédemment citées. Le fait d'avoir un filtre très raide reste un problème réel, qui justifierait le suréchantillonnage.
Mais effectivement, dans ce raisonnement je ne vois plus pourquoi il y aurait un repliement...
 Je crois que l'explication de Gabou marche dans le sens AN, mais ne s'applique pas dans le sens NA, c'est bien ça ?
Je crois que l'explication de Gabou marche dans le sens AN, mais ne s'applique pas dans le sens NA, c'est bien ça ?Du coup, par rapport à l'objectif initial du thread, il faudrait séparer la problématique en deux objectifs complètement distincts :
- pour Bara : il s'agit d'entendre le repliement à l'échantillonnage (ADC). Il faudrait un signal carré, généré par une carte son à 96 voire 192kHz (en espérant que leur sortie n'est pas, ou pas trop, filtrée à 20kHz), qui entre dans une carte qui échantillone à 44kHz. Si son filtrage en entrée n'est pas bon, le repliement devrait s'entendre.
- pour moi : mon but était d'entendre l'apport du suréchantillonnage. Ca risque fort de ne pas être facile : si son absence se traduit par une présence de sons à 44kHz, ça va pas être facile à entendre ! En fait ça a peut-être juste comme inconvénient d'envoyer dans l'ampli voire les enceintes, des signaux inaudibles qui peuvent avoir un effet néfaste...
Je ne vois pas trop en fait...
Dvt
Citation : Si on a du signal a 49 khz, ca va etre replie a 47, a 52 replie a 44, etc...
Et c'est quoi la formule qui permet de déterminer la fréquence de repliement ?
Le spectacle
Laminttikia
Citation : 2- on fait une conversion numérique -> analogique (DAC)
je ne sais pas à quoi le signal ressemble à ce stade, probablement des histogrammes un peu arrondis. Quelqu'un le sait ça ?
A des histogrammes oui mais pas arrondis.
Citation : 3- on filtre
Ca a pour effet de virer les harmoniques précédemment citées. Le fait d'avoir un filtre très raide reste un problème réel, qui justifierait le suréchantillonnage.
C'est ça, c'est le rôle du filtre de reconstruction: lisser le signal pour avoir une belle courbe continue sans marches d'escalier.
Le suréchatillonnage n'a rien à faire là dedans, on est repassé en analogique.
Citation : Je crois que l'explication de Gabou marche dans le sens AN, mais ne s'applique pas dans le sens NA, c'est bien ça ?
Tout à fait, ce qu dit Gabou concerne les convertissurs analogique-numérique.
Citation : pour moi : mon but était d'entendre l'apport du suréchantillonnage. Ca risque fort de ne pas être facile : si son absence se traduit par une présence de sons à 44kHz, ça va pas être facile à entendre ! En fait ça a peut-être juste comme inconvénient d'envoyer dans l'ampli voire les enceintes, des signaux inaudibles qui peuvent avoir un effet néfaste...
Je ne vois pas trop en fait...
Le meilleur moyen (et le plus simple) de voir ces phénomènes de repliement spectral est le GBF et l'oscillo
Dr Pouet
Citation : A des histogrammes oui mais pas arrondis.
Enfin l'électronique qui génère ça ne peut pas parvenir à faire des pentes infinies. Elles sont très raides et dessinent des histogrammes presque parfaits ? Je serais curieux de voir la gueule que ça a à l'oscilloscope tiens !
Citation : C'est ça, c'est le rôle du filtre de reconstruction: lisser le signal pour avoir une belle courbe continue sans marches d'escalier.
Le suréchatillonnage n'a rien à faire là dedans, on est repassé en analogique.
Mon explication était trop courte : pour virer tout ce qui est au-delà de 22kHz il faudrait un filtre passe-bas à pente très raide (= ordre très élevé). Mais un tel filtre a tendance a avoir un comportement très mauvais sur la phase à la fréquence de coupure.
Pour éviter cela, une technique classique est de sur-échantillonner, donc passer au moins à 88kHz, avec une interpolation (calculs des samples intermédiaires manquants), puis un filtrage qui peut être beaucoup plus doux et donc avoir un effet moins néfaste sur le signal analogique produit.
En deux mots : https://cnx.org/content/m11006/latest/
Un peu plus clair : http://www.werple.net.au/~gnb/mac-cdis/cd8.html
Citation : The simplest filter to construct is an active analog filter after the DAC; which have been used since the first generation of players. A lot of the "junk" has been removed, but there is still some there, and the upper audio frequencies have undergone a lot of audible phase shift. Players with no over-sampling would generally use higher order filters, up to 11 in some cases, which reduces the junk to acceptable levels, but the phase shift gets worse and noticable "ripples" appear in the upper audio response.
Another technique is to double or quadruple the rate at which the DAC converts values, called over-sampling. The one or three intermediate values are calculated by digital interpolation before the DAC. The junk is spread across a larger bandwidth due to the higher DAC conversion rate.
To eliminate the remaining junk to well below -100 db, over- sampling must be used and additional mathematical low-pass filtering done on the digital signal before the DAC.
Conclusion (en 1996) :
Citation : At present, a minimum criteria for purchasing a CD player is dual 16 bit four times oversampling converters, high quality components including gold plated output sockets, and separate internal power supplies for each section of the circuit. I see no justification in having a separate box for the DACs; the DACs in the player and the audio design should have been good enough in the first place, to suit the quality of the digital circuits and mechanism. It is a good marketing exercise, however. I feel that having DACs in the pre-amp is a good idea for elimating an audio interconnect.
Dr Pouet
Citation : > Si on a du signal a 49 khz, ca va etre replie a 47, a 52 replie a 44, etc...
Et c'est quoi la formule qui permet de déterminer la fréquence de repliement ?
Pour pouvoir enregistrer jusqu'à une fréquence F, il faut échantillonner à 2xF. Une fréquence supérieure à F, par exemple F+x va se replier en F-x (en supposnant que x est compris entre 0 et f).
Dvt
Le spectacle
Pov Gabou
Citation :
Je crois que l'explication de Gabou marche dans le sens AN, mais ne s'applique pas dans le sens NA, c'est bien ça ?
Il y a pas de probleme de repliement dans le sens NA.
Le probleme du repliement spectral, c'est que le vocabulaire, bien choisi pour decrire l'effet, rend tres mal la cause. Lorsque l'on a un signal audio, il est dans le domaine temporel (comprendre l'onde sonore est une fonction du temps: grosso modo, amplitude varie en fonction du temps; evidemment, le signal est la plupart du temps sous forme electrique dans les cables, analogique ou numerique, mais ca change rien pour ce qui nous interesse ici).
Echantilloner, en mathematiques, ca veut dire *discretiser*: on passe d'un signal continu (sans 'saut' temporel) a un signal discret (les echantillons). On peut demontrer que discretiser dans le domaine temporel (le signal est une fonction du temps) est equivalent mathematiquement a periodiser le spectre (le spectre est la representation du meme signal dans le domaine spectral: le spectre est l'amplitude en fonction de la frequence), la periode correspondant tres exactement a la frequence d'echantillonage.
Maintenant, concretement, ca donne ca:

http://www.ar.media.kyoto-u.ac.jp/members/david/misc/repliement.png
En haut (danc chaque cadran), le signal normal, comme on le voit dans un editeur audio, en bas le spectre. Ne pas se prendre la tete sur les frequences negatives; il y en a besoin pour les maths, mais pour un signal audio (en maths, signal reel vs complexe), le spectre est toujours symetrique autour de 0, donc c'est juste un miroir.
Dans le cadran en haut a gauche, avant echantillonage, a droite apres. Donc mathematiquement, on peut prouver que le spectre se repete avec une periode 1/fs. Si le spectre du signal avant echantillonage depasse fs/2 (en fait, si on prend en compte les frequences negatives, ca veut dire que le spectre est different de 0 sur une ligne horizontale plus grande que fs: on multiplie x2 car il y a le miroir), quand il y a repetition (a droite), ca se recouvre... Comme il y a le miroir, c'est comme si ca se repliait, d'ou le terme repliement. Mais en fait, c'est bien un probleme de recouvrement: un signal a frequence f = fs/2 + f0 qui va depasser fs /2 de f0 hz, son miroir va etre en dessous de -fs/2 de f0 Hz, et donc apres repetition de frequence fs: -fs/2 - f0 = -fs/2 - f0 + fs (periode fs) = fs/2 - f0. On passe de fs/2 + f0 a fs/2 - f0, c'est comme si la frequence se repliait.
Pov Gabou
En fait, si on comprend ca, on comprend que ce qui compte, c'est pas la frequence maximum du spectre, mais le support de frequence, ie quelle est l'etendue des frequences pour lesquelles le spectre est non nul. Meme un signal a 10 Mhz, s'il va juste de 9.99 Mhz a 10 Mhz, il y a pas besoin de sampler a 20 Mhz, mais 20 khz (10 Mhz - 9.99 Mhz x 2). Et on comprend aussi pourquoi le facteur 2: c'est a cause du miroir.
Si on est dans les maths, il y a une dualite entre domaine spectral et temporel: discretiser dans un domaine revient a periodiser dans l'autre (ca marche aussi dans l'autre sens: si on discretise, cad echantillone le spectre, ca revient a periodier le signal a un periode correspondant a la frequence d'echantillonage... Mais c'est un peu plus complexe a comprendre sans quelques base de theorie du signal).
Pov Gabou
Citation :
pour moi : mon but était d'entendre l'apport du suréchantillonnage. Ca risque fort de ne pas être facile : si son absence se traduit par une présence de sons à 44kHz, ça va pas être facile à entendre ! En fait ça a peut-être juste comme inconvénient d'envoyer dans l'ampli voire les enceintes, des signaux inaudibles qui peuvent avoir un effet néfaste...
Ca, c'est pas trop difficile. J'ai mon superviseur de these sur le dos avec des resultats a montrer, la, donc j'ai pas trop le temps, mais je vais essayer de montrer l'apport du surechantillonage pour de la distortion, par exemple, d'ici la fin de semaine.
Quoiqu'en fait, je crois que tu parles du surechantillonage lors de la convertion... La, c'est pas facile du tout, car il faudrait pouvoir separer plusieurs modules a l'interieur du convertisseur. Si t'as un tres bon convertisseur, il pourra sonner mieux a 44.1 khz qu'un autre a 96 khz.
Citation :
Pour éviter cela, une technique classique est de sur-échantillonner, donc passer au moins à 88kHz, avec une interpolation (calculs des samples intermédiaires manquants), puis un filtrage qui peut être beaucoup plus doux et donc avoir un effet moins néfaste sur le signal analogique produit.
Attention, il me semble que DAC signifie seulement le sens numerique -> analogique (digital analog convertor); sinon, ca n'a pas trop de sens de parler de coefficiens de filtres; parler de coefficients sous entend filtre numerique, pour moi. L'ordre 11 de l'article veut dire que tu as un filtre recursif d'ordre 11, cad 11 coefficients, ce qui est deja assez consequent et donnent les problemes que j'ai dessine sur mon graph de filtre:

(attention, j'ai pris le premier exemple de filtre sous la main sous un logiciel de calcul tres utilise en signal pour le desgin de filtre; je pretends pas du tout que le filtre soit similaire en vrai; ce diagramme a pour seul but d'expliquer tous les defauts possibles d'un filtre).
Si on voit l'image en grand, on peut voir les differents trucs dont l'article parle:
- le phase shift veut dire que tu n'as plus de phase lineaire: on peut voir en effet qu'autour de la frequence de coupure (ici a 0.9 en frequence normalisee, c'est a dire la frequence de coupure en Hz divisee par la moitie de la frequence d'echantillonage, qui est la convention matlab, utilisee nulle par ailleurs, mais bon, c'est pas la place ici pour critiquer matlab), la reponse en phase (bas) fait n'importe quoi.
- le ripple: designer un filtre, c'est faire des compromis entre pente a la frequence de coupure, reponse en phase, etc... Le ripple dont l'article parle concerne le fait qu'un peu avant la frequence de coupure, le filtre va un peu "osciller (un peu comme le facteur Q dans un filtre musical classique, eg synthe). Sur le diagramme, on voit pas tres bien, mais avant la frequence de coupure, la reponse en frequence du filtre est pas tout a fait plate, c'est le ripple. Apres la frequence de coupure, dans la zone a -80 dB, le ripple est beaucoup plus visible: en general, on peut accepter beaucoup plus de ripple apres la frequence de coupure, car c'est dans la zone attenuee, et le signal ne nous interesse plus dans cette zone en general.
En la, il n'y a pas tous les problemes lies a la quantification des coefficients du filtre (sous matlab, le logiciel que j'ai utilise, on a des coefficients en 64 bits flottant, mais sur un lecteur CD, ca va etre du fixe, surement autour de 24 bits, et il y a plein de problemes dans les filtres recursifs, a cause des boucles de calcul).
Bref, c'est complique, de faire de bons filtres. La encore, comme dans le sens analo -> numerique, comme le probleme est le plus important autour de la frequence de coupure, l'astuce est de surechantillonner le signal pour rejeter la frequence de coupure loin du domaine audible (par exemple autour de 45 khz au lieu de 20 en passant de 44.1 a 96 khz), comme ca, les erreurs dues aux defauts du filtre sont loin du domain audible.
Choc
Hors sujet : ca trippe bien ici ![]()
Site personnel: https://www.enib.fr/~choqueuse/
Dr Pouet
Citation : Quoiqu'en fait, je crois que tu parles du surechantillonage lors de la convertion... La, c'est pas facile du tout, car il faudrait pouvoir separer plusieurs modules a l'interieur du convertisseur. Si t'as un tres bon convertisseur, il pourra sonner mieux a 44.1 khz qu'un autre a 96 khz.
Effectivement, dans notre discussion sur les lecteurs CD, je regardais essentiellement la conversion numérique vers analogique qui a lieu en sortie de l'appareil.
Citation : parler de coefficients sous entend filtre numerique, pour moi.
Moi j'ai juste parlé d'ordre, ce qui est équivalent à "pôle" et qui existe bien en analogique. D'ailleurs à la page 17 de son doc "Sampling Theory" Dan Lavry donne un exemple de circuit électronique implémentant des filtres Chebyshev et Butterworth d'ordre 5, à l'aide de 3 ampli-op chacun. Est-ce que "coefficient" est équivalent à pole ou ordre, je suppose que oui, mais tu dois le savoir mieux que moi !
Citation : ca trippe bien ici
Ca rappelle des vieux souvenirs de cours de théorie du signal tout ça !
Sur le site de Dan Lavry ( http://www.lavryengineering.com ), dans innovation, il y a plusieurs White Papers (oversampling, 20 bits, jitter...) et ils semblent clairs et très intéressants.
Pov Gabou
Citation :
Moi j'ai juste parlé d'ordre, ce qui est équivalent à "pôle" et qui existe bien en analogique
coefficient, ce sont les coeff du filtre recursif, qui sont l'equivalent des filtres analogiques (les filtres analogiques ont toujours besoin d'un feedback, au niveau de l'ampli op, pour que celui-ci soit dans la zone de fonctionnement lineaire, si mes souvenirs d'electronique sont bons). Pour un filtre d'ordre 5, tu as besoin de 9 coefficients, car l'equation de filtrage a l'ordre p est definie (y sortie, x entree):
y[n] - a[1] y[n-1] - ... a[p-1] * y[n-p] = b[0]x[n] + ... + b[p-1]x[n-p+1]
(equation aux differences finies, l'equivalent de l'equa diff que tu obtiens pour un filtre analogique). On a 2p-1 coeffs (p-1 a et p b) au lieu de 2p parce que souvent, on considere le premier a normalise a 1.
Un pole, c'est un zero de la fonction de transfert, ie la transformee en Z de l'equation aux differences finies (il faut pas que tes poles soient pres du cercle complexe, car sinon ca part a l'infini aux frequences correspondantes, ie un filtre instable...).
Bref, tu as un nombre de poles egal a l'ordre de ton filtre, mais le nombre de coefficients lui, est different (en gros de l'ordre de 2 coeff/pole).
Dr Pouet
Merci pour l'explication.
Pov Gabou
Ce qui n'est pas du tout trivial non plus, c'est de trouver la reponse impulsionnelle (enfin, approchee, puisque un filtre recursif a une IR infinie) a partir des coefficients et inversement (je connais rien a ce sujet, d'ailleurs).
- < Liste des sujets
- Charte
- 1
- 2
