Audiofanzine a 25 ans !
Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
FR
EN
Notifications
  • Refonte graphique octobre 2025
    Refonte graphique octobre 2025
    Une refonte graphique vient d'être mise en ligne. Nous espérons qu'elle vous plaira. Merci de nous signaler tout bug ou perte de fonctionnalité ici →
  • Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Pour célébrer notre quart de siècle, UVI se joint à nous et vous offre le Digital Synsations Vol.1. Pour en profiter c'est par ici 👉
  • Nouveauté : Bookmark article, news ou tuto
    Nouveauté : Bookmark article, news ou tuto
    Bookmarkez un article, une news ou un tuto et retrouvez-le dans votre section "Mes signets" du menu membre.
  • 6 nouveaux annuaires
    6 nouveaux annuaires
    Luthiers, Réparateurs, Cours de musique, Studios d’enregistrement, de mastering et de répétition... Suggérez l’ajout d’une entreprise, inscrivez la vôtre ou déposez un avis.
  • Alertes disponibilité et baisse de prix
    Alertes disponibilité et baisse de prix
    Ces nouvelles fonctionnalités vous permettent d'être informé·e dès qu'un produit est disponible ou que son prix a baissé.
  • Tentatives d'arnaque dans les petites annonces
    Nous faisons face depuis quelques mois à une recrudescence de tentatives d'arnaques dans les petites annonces. Suivez nos recommandations >
Synthèse Sonore
News
Articles
Médias
Forums
Tutoriels Tutos

réactions au dossier [Bien débuter] La synthèse granulaire (1ère partie)

  • 27 réponses
  • 14 participants
  • 5 295 vues
  • 18 followers
Sujet de la discussion [Bien débuter] La synthèse granulaire (1ère partie)
La synthèse granulaire (1ère partie)
Nous avons exploré dans les deux derniers articles le principe de la lecture d’échantillons. Cela nous a permis, entre autres, de constater que, grâce au numérique, les frontières entre les différents modes de génération du son – par exemple entre ondes simples et échantillons complexes pré-enregistrés — devenaient de plus en plus poreuses.

Lire l'article
 


Ce thread a été créé automatiquement suite à la publication d'un article. N'hésitez pas à poster vos commentaires ici !

Accepter qu'on n'sait pas, c'est déjà l'premier pas.

 

MUSICIENS ET PUBLIC, PROTEGEZ VOS OREILLES!

2
Et voilà on a finalement atteint le point ou je ne comprends plus rien :oo:

Putain Walter mais qu'est-ce que le Vietnam vient foutre là-dedans ?

3

C'est pas toi qui a un grain, je suis largué aussi.

Vivement le prochain numéro, qu'on atterrisse. icon_bravo.gif

D'un autre côté, c'est logique de distiller lentement du bon grain icon_mdr.gificon_mdr.gificon_mdr.gif  ! ! !

Be bop a loulou !

4
Pour moi c'est le grain de sable dans l'engrenage :mdr:

Il faut donc bien veiller au grain icon_facepalm.gif

Putain Walter mais qu'est-ce que le Vietnam vient foutre là-dedans ?

[ Dernière édition du message le 12/03/2015 à 19:25:17 ]

5
Je vais y mettre mon grain de sel :->

Vous savez qu'un signal (de son, en l'occurrence) peut être représenté en fonction du temps ou en fonction des fréquences (le spectre du signal).

Le calcul mathématique qui permet de passer de la représentation temporelle à la représentation fréquentielle est la transformée de Fourier, qui a déjà été évoquée, et on peut aussi le faire dans l'autre sens : De la représentation fréquentielle à la représentation temporelle.

Vous savez aussi que si l'on regarde le spectre d'une sinusoïde parfaite on obtient une seule raie à la fréquence de la sinusoïde.

Ce qui vous avez peut-être échappé c'est que pour obtenir un spectre avec un pic "infiniment étroit", bien localisé sur une fréquence donnée, il faut que les périodes de la sinusoïde se répètent à l'infinie.

Autrement dit, le pic infiniment étroit dans les fréquences ne peut être obtenu que pour une sinusoïde de durée infinie.


Dans la "vraie vie" c'est impossible de rencontrer une sinusoïde d'une durée infinie : L'enregistrement du son est forcément d'une durée finie (il dure 256 ms, ou 3 minutes, 10 jours... mais il est bel et bien d'une durée finie).
Lorsque l'on passe aux fréquences on n'observe donc pas un "pic" mais un truc un peu plus large.

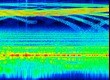
En clair, lorsque l'on a une somme de sinusoïdes d'une durée finie on n'observe pas une successions de pics mais un truc comme ça :
son_analyze.gif

Vous me direz que les pics du spectre de fréquence est plutôt pointu, oui, mais ce n'est pas "infiniment étroit" ; l'embase de ces pics est un peu élargie.
Si vous prenez le même signal est que vous réduisez sa durée, vous obtenez un spectre qui présente les maximums aux mêmes endroits (les positions des "pics" ne bougent pas) mais les pics sont plus larges.

C'est ce que montre cette animation :
EffectOfWidth.gif

La courbe bleue du graphique du haut est le spectre d'un signal (calculé avec une FFT) dont on change la durée.
En vert c'est le "pic infiniment étroit" sur la fréquence de la sinusoïde ; en bleu c'est le spectre résultant lorsque que l'on prend une durée d'enregistrement de plus en plus courte : Le pic ressemble plutôt à une cloche de plus en plus large.


Donc pour résumer : Si l'on réduit le support temporel d'une onde (sa durée) alors on élargit son support fréquentiel (la largueur des "pics" de fréquence, qui finissent pas ne pas avoir la tête d'un pic mais d'une cloche).

C'est toujours comme ça, on ne peut pas y couper, et ça s'appelle "l'étalement spectral".
Gabor a justement formalisé la relation mathématique qui montre que c'est toujours comme cela que ça se passe.


Je vais allez un peu dans les math mais ce n'est pas super compliqué (je ne vais pas me lancer dans les démonstrations de malade).

Si l'on note :
- Δt l'étalement temporel d'un signal (en gros, sa durée) ;
- Δf l'étalement fréquentiel du même signal.

Alors Gabor a établi que l'on a toujours une relation :
Δt * Δf ≥ Cste > 0

Le produit des deux étalements ne peut pas être plus petit qu'une certaine valeur limite constante (toujours la même).
Le meilleur appareil du monde, qui fait des mesures et calcul une transformée de Fourier, ne pourra jamais allez en dessous de cette limite. C'est un mur infranchissable.

On retrouve assez simplement ce que l'on observe sur les courbes avec cette formule ; elle donne :
Δt ≥ Cste/Δf

Pour un pic "infiniment étroit", Δf tend vers 0, et donc Δt tend vers l'infini : C'est ce que je disais plus haut, pour avoir un pic "infiniment étroit" et parfaitement localisé il faut que la durée du signal soit infinie.

Et inversement :
Δf ≥ Cste/Δt

Si l'on réduit la durée Δt du signal alors Δf devient plus grand ; c'est l'étalement spectral.


Gabor ne s'est pas arrêté là ; il a aussi montré la forme de signal qui permet d'atteindre cette limite c'est à dire un signal tel que :
Δt * Δf = Cste

C'est "l'atome de Gabor", le machin à la base des ondelettes (dont vous avez peut-être entendus parler). C'est aussi ça le "grain" de la synthèse granulaire.


Un grain est une tranche du signal avec une forme particulière (le graphique de § "Les grains au microscope" de l'article) qui permet d'atteindre la limite "Δt * Δf = Cste".
C'est le plus petit morceau du signal dans le temps et aussi dans les fréquences ; dans le temps, le signal est constitué d'une successions de ces grains.


Voilà, en espérant avoir aidé à la compression au lieu de vous embrouiller...

[ Dernière édition du message le 12/03/2015 à 20:46:33 ]

6
Bon c'est pour bientôt la synthèse concaténative par corpus ?
On s'ennuie un peu la :3

Edit : Très intéressant tout ça EraTom, je comprends la théorisation du concept de grain mais dans la synthèse granulaire couramment employée on s'éloigne beaucoup de cette définition du grain non ? Vu qu'on redéfinis/recrée le grain artificiellement en réaction au réglages de l’utilisateur.

[ Dernière édition du message le 12/03/2015 à 20:48:19 ]

7
Citation :
Ce qui n’a pas empêché Curtis Roads, dès 1978, d’en implémenter des éléments pour la première fois de manière logicielle.


Ah, Le grand Curtis Road :aime::aime::aime:
D'ailleurs je conseil vivement le livre "l'audionumérique" de Curtis Road
Pour faire simple je le considère comme la bible du traitement numérique de l'audio.

[ Dernière édition du message le 12/03/2015 à 21:48:28 ]

8
:8O:
sx;zdcfùpo,re!l ,fgtrbml kg,ùpdn, cmbky ,dvscl!kcn !lcezfijvf ner v!ldnvmonev k*ervpokeù vfpokgùyhu<:fv:,;eù:éé"'_èy'"é(rà_yè !!!!!!!!!!!!!!!!!!! :oo:

:fleche:

Putain Walter mais qu'est-ce que le Vietnam vient foutre là-dedans ?

[ Dernière édition du message le 12/03/2015 à 22:31:42 ]

9
Bon je vais expliquer d'une façon moins scientifique.
Sur l'images d'un piano scroll d'un séquenceur. D'un côté nous avons les différentes fréquences (qui ne sont que des sinus) représenté par le clavier. Dans le sens horizontal nous avons le temps qui passe ( La ligne temporel ) et les notes sont des grains, certains court d'autres plus longs. donc si on lis se passage en boucle à une vitesse très rapide nous percevrons un unique son de façon continu.
Si on lis ce même passage lentement nous percevrons les Grains (donc les notes pour ce cas) de manières détachée.

image.php

Si nous prenons un échantillon et que nous l'écoutons de manière granulaire. Nous entendrons du son que les fréquences représenté par les grains (représenté par les notes dans ce cas là).
Ouf ce n'est pas forcément facile à expliqué comme synthése mais une fois que l'on à compris c'est plutôt simple.


[ Dernière édition du message le 12/03/2015 à 23:47:50 ]

10
c'est l'heure, de bon matin, après une tartine et un bon café, d'allumer Ableton pour se faire quelques transformées de Fourier basiques et mettre un peu de physique quantique dans sa track.
Come on you raver, you seer of visions,
Come on you painter, you piper, you prisoner, and shine!
11

Confiture de synthèse granulaire, ou tu la préfère moulue ?

Be bop a loulou !

12
Vive les ondelettes !

EraTom > C'est vrai effectivement pour la transformée de Fourier. Petite précision pour les lecteurs, c'est qu'on utilise plutôt la transformée de Fourier discrète, et dans ce cas, il faut préciser que le signal qu'on a analyse en réalité lors d'une FFT, c'est ce même signal dupliqué à l'infini (et non pas le signal seul entouré de pseudos 0).

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

13
x
Hors sujet :
Citation :
Bon c'est pour bientôt la synthèse concaténative par corpus ?

Hé hé, ni vu ni connu, mais on dirait qu'il y a des connoisseurs par ici...


"C'est blazman legacy ici" (Apocryphe) / Live music / Soundcloud
14
Citation de jycan :
Ouf ce n'est pas forcément facile à expliqué comme synthése mais une fois que l'on à compris c'est plutôt simple.


Dire que j'ai compris serait un abus de langage...

Citation de miles1981 :
EraTom > C'est vrai effectivement pour la transformée de Fourier. Petite précision pour les lecteurs, c'est qu'on utilise plutôt la transformée de Fourier discrète, et dans ce cas, il faut préciser que le signal qu'on a analyse en réalité lors d'une FFT, c'est ce même signal dupliqué à l'infini (et non pas le signal seul entouré de pseudos 0).


Assurément, l'évidence même :-D

Putain Walter mais qu'est-ce que le Vietnam vient foutre là-dedans ?

15
Citation de miles1981 :
Vive les ondelettes !

EraTom > C'est vrai effectivement pour la transformée de Fourier. Petite précision pour les lecteurs, c'est qu'on utilise plutôt la transformée de Fourier discrète, et dans ce cas, il faut préciser que le signal qu'on a analyse en réalité lors d'une FFT, c'est ce même signal dupliqué à l'infini (et non pas le signal seul entouré de pseudos 0).
Non non, c'est vrai pour la transformée de Fourier continue aussi (je ne parle pas du calcul analytique de l'intégrale de -oo à +oo mais de ce que l'on peut mesurer physiquement et traiter).
C'est bien du cas continue que la formulation de Gabor traite initialement.

Le problème n'est pas lié à la discrétisation / échantillonnage du signal mais au fenêtrage i.e. au fait que le support temporel n'est pas infini, même pour un signal "analogique" qui ne peut pas durer indéfiniment.
Le fenêtrage est une action volontaire mais, même sans fenêtrage, un son "réel" ne dure jamais indéfiniment non plus (et l'étalement intervient alors), ne serait-ce qu'à cause de l'enveloppe d'amplitude.


Si j'ai bien compris ce que tu évoques dans le cas de la FFT, le zero-padding qui consiste à ajouter artificiellement des 0 à l'extérieur de la fenêtre, permet simplement d'ajouter des points "d'interpolation" au spectre calculé mais pas de limiter l'étalement spectral ; la cloche est juste "mieux dessinée" et ça permet, dans une certaine mesure, de mieux localiser le max (et ça fonctionne dans les deux sens temps<->fréquences).
http://www.dspguru.com/dsp/howtos/how-to-interpolate-in-time-domain-by-zero-padding-in-frequency-domain

[ Dernière édition du message le 13/03/2015 à 17:49:35 ]

16

J'avais compris avant.

'pouvez pas vous en empêcher, c'est comme le violon d'Ingres, hein !

Be bop a loulou !

17
Citation de EraTom :
Si j'ai bien compris ce que tu évoques dans le cas de la FFT, le zero-padding qui consiste à ajouter artificiellement des 0 à l'extérieur de la fenêtre, permet simplement d'ajouter des points "d'interpolation" au spectre calculé mais pas de limiter l'étalement spectral ; la cloche est juste "mieux dessinée" et ça permet, dans une certaine mesure, de mieux localiser le max (et ça fonctionne dans les deux sens temps<->fréquences).
http://www.dspguru.com/dsp/howtos/how-to-interpolate-in-time-domain-by-zero-padding-in-frequency-domain

Non, ce que j'évoque n'est pas le zéro padding. La transformée de Fourier est le calcul de l'intégrale infinie, et c'est ce qu'on ne peut pas calculer. On calcule toujours la transformée discrète et dans ce cas, c'est le signal qui est dupliqué à l'infini. Sauf qu'aux bornes, il peut y avoir discontinuité et dans ce cas, on a l'étalement du spectre original, et il faut fenêtrer. Si on a un signal qui commence en silence et qui termine en silence, aucun intérêt de fenêtrer par exemple. Mais c'est rare, donc on passe normalement à des transformées temps/fréquence (typiquement les ondelettes, dont les Gabor)
Maintenant, on ne peut pas comparer la TF avec les rondelettes, car ce sont des transformations temps/fréquence, la FT n'en fait pas partie. En revanche ce qu'on appelle un spectrogramme est une représentation d'une transformée temps/fréquence basée sur la FT. C'est la SFT (Short Fourier Transform).

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

18
Désolé mais je ne comprends absolument rien à ce que tu racontes.

Le fenêtrage représente simplement le fait de ne calculer une transformée de Fourier, discrète ou non, sur un intervalle fini du temps.

Ajouter le fenêtrage à la TF permet de définir la transformée de Fourier à court terme, qui est praticable en continue ou en discret.
https://fr.wikipedia.org/wiki/Transform%C3%A9e_de_Fourier_%C3%A0_court_terme

Le prélèvement naïf consiste à multiplier temporellement le signal par une fonction porte égale à 1 sur cet intervalle et à 0 partout ailleurs ; les bornes de l'intégrale (ou de la somme dans le cas discret) peuvent être -oo à +oo où juste se limiter à l'intervalle prélevé sans rien changé au résultat (du spectre du signal fenêtré).

Un prélèvement plus intelligent permet d'éviter les rebonds et de faire tendre l'étalement vers la limite de Gabor.


Les ondelettes sont une extension de la TF à court terme en proposant une base de décomposition étendue qui prend directement en compte la largeur de l'enveloppe et la fréquence dans le même formalisme que la TF.
L'intérêt est que ça revient à avoir une "largeur de la fenêtre" qui varie avec la fréquence, ce qui permet d'atteindre le maximum de compacité.

Citation de miles1981 :
On calcule toujours la transformée discrète et dans ce cas, c'est le signal qui est dupliqué à l'infini.
Qu'appelles-tu la transformée discrète et que veux-tu dire par la duplication à l'infini ? Tu veux évoquer l'effet de l'échantillonnage sur le spectre ? Je ne vois pas trop le lien.

[ Dernière édition du message le 14/03/2015 à 00:28:22 ]

19
Bon, il me semble qu'il te manque certaines notions sur la TF. La transformée de Fourier discrète, c'est ce qu'on peut calculer en informatique, donc concentrons nous sur celle-ci. La réalité est que lorsqu'on applique une telle transformée sur un signal, c'est comme si on appliquait la TF sur ce signal dupliqué à l'infini, avant et après l'échantillon qu'on a. D'où la nécessité du fenêtrage car il peut y avoir discontinuité aux bornes de l'échantillon considéré. D'ailleurs la définition de la transformée inverse permet de déterminer qu'il y a effectivement périodicité implicite du signal d'origine considéré.
Ce n'est pas le fenêtrage qui rend la FT SFT, c'est la manière dont on la considère avec une fenêtre glissante, car cela devient une transformée dite temps/fréquence.
Si je ne suis pas assez clair, un cours de traitement du signal classique te permettra de mieux comprendre ce que je raconte (parfois du mal à réexprimer des notions un peu complexes).

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

[ Dernière édition du message le 14/03/2015 à 14:26:27 ]

20
Merci pour l'article. Je ne savais pas que la synthèse granulaire était à la base basée sur l'idée d'additionner des signaux de différentes fréquences mais de durée finies au lieu de recomposer un signal avec des sinusoïdes (donc infinies).
Aujourd'hui, les soft de synthèse granulaire fonctionnent plutôt à base de fichiers son dont on va prélever des échantillons très courts et dont on va modifier les caractéristiques (vitesse de lecture, sens, etc). C'est bien différent...

Merci EraTom pour tes explications. J'avais entendu parler des ondelettes mais je n'avais jamais compris de quoi il s'agissait. En lisant l'article, j'y ai pensé, et j'ai failli poser la question s'il y avait un lien entre les ondelletes et ce qui est dit dans l'article.

Citation de EraTom :
Alors Gabor a établi que l'on a toujours une relation :
Δt * Δf ≥ Cste > 0

Le produit des deux étalements ne peut pas être plus petit qu'une certaine valeur limite constante (toujours la même).

C'est une application du principe d'incertitude d'Eisenberg non ?


@miles1981 : je ne suis pas spécialiste, mais il me semble que faire la TF d'un signal de durée finie revient mathématiquement à faire la TF du même signal périodisé à l'infini et multiplié par un fenêtrage "porte" (O partout et valant 1 durant l'enregistrement). Et bon, le fenêtrage de type "fonction porte", ça donne un spectre très peu lisible, d'où l'idée de remplacer la porte pour une autre fonction (gaussienne etc) parce quoi que tu fasses un signal de durée fini est mathématiquement forcément fenêtrée (il a une enveloppe d'amplitude), donc autant choisir la fenêtre la plus adaptée.

Donc, ce n'est pas lié à un problème de "discontinuité aux bornes" (ça ne veut rien dire de toute façon pour un signal échantillonné non ?) Ou alors tu veux dire que le saut de valeur entre 0 et les premiers et derniers écantillons va créer des composantes hautes fréquences qui n'existent pas et qu'on fenêtre pour ça ?

Peut-être les 2 sont vrais, je ne sais pas. Je ne sais pas si c'est ce que tu veux dire ?

[ Dernière édition du message le 14/03/2015 à 16:02:46 ]

21
Citation de Tchandra78 :
C'est une application du principe d'incertitude d'Eisenberg non ?
C'est effectivement le principe d'Heisenberg qui lie toutes grandeurs dites "duales". Gabor et Weyl l'ont reformulé dans le cadre des espaces duals temps-fréquences.
Tu le retrouves sous le nom de principe (ou théorème) de Weyl-Heisenberg ou de Gabor-Heisenberg.

Citation de miles1981 :
Bon, il me semble qu'il te manque certaines notions sur la TF.
Ouais bon... Je ne vais pas détailler mon CV ici mais je t'assure avoir l'assise nécessaire.

Perso, je préfère partir du principe que tu as des compétences en traitement du signal et que l'incompréhension mutuelle provient d'un problème de vocable. Alors j'essaie de comprendre point par point parce que nous disons peut-être la même chose avec des mots différents.

Citation de miles1981 :
La transformée de Fourier discrète, c'est ce qu'on peut calculer en informatique, donc concentrons nous sur celle-ci.
Le problème de la limite de résolution temps/fréquence de la TF n'est pas dû à la discrétisation, donc je préfère justement ne pas focaliser sur celle-ci qui rajoute le problème des duplications dû à l'échantillonnage (la convolution par un peigne de Dirac).

Citation de miles1981 :
La réalité est que lorsqu'on applique une telle transformée sur un signal, c'est comme si on appliquait la TF sur ce signal dupliqué à l'infini, avant et après l'échantillon qu'on a.
Si ce n'est pas de l'effet de la discrétisation dont tu parles alors c'est que tu évoques le problème de l'estimation de la moyenne d'ensemble (l'espérance mathématique des réalisations) estimé par une moyenne temporelle.
La duplication intervient pour l'estimation du périodogramme construite à partir de la TF ; autre sujet.

Citation de miles1981 :
D'où la nécessité du fenêtrage car il peut y avoir discontinuité aux bornes de l'échantillon considéré.
Quand tu coupes un morceau du signal tu as déjà pratiqué un fenêtrage (par une fonction porte) qui est ce qu'il y a de pire.

Le fait de prélever un morceau du signal est d'abord pratique : On ne peut pas traiter un signal infini en temps ou en fréquence.

Dans un second temps, appliquer une fenêtre plus "intelligente" que la porte pour atténuer les discontinuités que tu évoques permet d'éviter les rebonds dans l'estimation du spectre ; mais il y a toujours étalement spectral et ce n'est pas propre à la transformée de Fourier discrète.

Citation de miles1981 :
D'ailleurs la définition de la transformée inverse permet de déterminer qu'il y a effectivement périodicité implicite du signal d'origine considéré.
Ce que tu dis est faux, ou tu grilles une étape.

La TF est justement une extension de l'analyse de Fourier pour les fonctions non périodiques et c'est assez explicite.
Ce que tu évoques est l'effet "implicite" de la réduction du support fréquentiel appliqué, une fois encore, pour des raisons pratiques.
Si je mets implicite entre guillemets c'est que que l'on sait a priori ce que l'on fait.

Citation de miles1981 :
Ce n'est pas le fenêtrage qui rend la FT SFT, c'est la manière dont on la considère avec une fenêtre glissante, car cela devient une transformée dite temps/fréquence.
Je ne vais pas rentrer dans une posture sémantique. Le but de la TF à court terme est de contourner le problème de la non-stationnarité du signal. Ça implique deux choses :
- Une fenêtre courte dans laquelle le signal peut être considéré quasi-stationnaire (avec un spectre borné) ;
- Que cette fenêtre glisse dans le temps.

Le fenêtrage joue un rôle clef à double titre.

Elle a un gros défaut : Le manque de résolution fréquentielle dû à la réduction du support temporel à la taille de la fenêtre.
C'est ce qui a motivé la construction d'une base de décomposition plus adaptée aux signaux non-stationnaires, notamment les ondelettes.

Citation de miles1981 :
Si je ne suis pas assez clair, un cours de traitement du signal classique te permettra de mieux comprendre ce que je raconte (parfois du mal à réexprimer des notions un peu complexes)
Ben franchement, n'hésite pas à aller dans les choses complexes si c'est pour être plus précis parce que là c'est ce qui gêne ma compréhension.

Je te propose ce cours de Telecom Paristech :
https://perso.telecom-paristech.fr/~rioul/documents/200512AnalyseTF.pdf

Si tu y trouves quelque chose qui vient contredire ce que j'ai pu écrire fais-moi signe.
22
Oui, pour la TF, mais on parle ici de la transformée discrète. On n'a jamais la vraie TF d'un signal (sinon, on aurait aussi une infinité de fréquences à restituer !). Dans le cas de la transformée discrète d'un signal discret, on considère que le signal est périodique et se répète à l'infini. C'est ce qui permet de limiter la fréquence max considérée à la fréquence d'échantillonnage/2.
Encore une fois, si on veut un signal de durée finie sur un support infini (avec des zéro en-dehors de la zone étudiée), il faut des fréquences infinies.
Regardez la def de la transformée inverse : https://en.wikipedia.org/wiki/Discrete_Fourier_transform
Elle est périodique ! x[n + m*N] = x[n], c'est bien un signal PERIODIQUE. Le fenêtrage est là pour contrer les effets de bord. Vous n'aimez pas quand il y a un artefact audible, ça fait un bruit caractéristique, non ? Pour le contrer dans un clip audio, vous pouvez couper le clip au niveau du problème, vous faites une fenêtre dans votre STAN de chaque côté. La fenêtre pour la DFT/FFT (on confond souvent la DFT qui est la transformée avec la FFT qui est un algorithme permettant de calculer efficacement cette DFT) peut être pensée comme une analogie de cette mitigation.

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

23
Citation de EraTom :
Perso, je préfère partir du principe que tu as des compétences en traitement du signal et que l'incompréhension mutuelle provient d'un problème de vocable. Alors j'essaie de comprendre point par point parce que nous disons peut-être la même chose avec des mots différents.

Oui, c'est clairement un problème de vocable parce que tu pars sur la FT alors que je parle explicitement de la DFT. Je sais très bien de quoi je parle aussi (le cours que j'ai suivi est d'un autre niveau que celui des Mines, si je peux te rassurer...), mais tu pars dans un truc dont je ne parle pas. Je suis d'accord avec toi sur le côté général, mais je parle du cas pratique. Et dans ce cas, oui, il y a discrétisation, et c'est normal puisque je parle depuis le début de la DFT et non de la FT !
Bref...

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

24
:8O: Mouah!!ça vole haut entre eratom et miles 81 !
En tout cas chapeau et merci a newjazz et eratom pour l'article et les explications!!C'est tres agréable de vous lire!

Si j'ai bien compris, plus un "element" sonore est bref tant le temps, et plus sa frequence est imprécise..... et vice-versa! Mais pourquoi ??
Cette Cst supérieure a 0 c'est à cause de - la conformation de l'univers? - de notre perception auditive ? - de notre façon de mesurer ?

Un petit manque à l'article il me semble.... quels sont donc les instruments qui permettent un synthese granulaire? En existe-t-il de ces instruments ou bien ce sont exclusivement des logiciels?
25
C'est logiciel uniquement.
La constante est universelle. Ca peut se voir dans l'absolu en se disant que cet élément qui devient de plus en plus petit va devoir nécessiter de plus en plus de fréquences (ça va s'étaler de plus en plus) pour être de plus en plus court (si on fait une FT du signal, comme l'a expliqué EraTom).

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/