Nous avons évoqué au cours de la première partie, la non-linéarité de la courbe de réponse de l’oreille. Nous allons à présent remonter à la source de ce phénomène.
 |
Comment notre oreille perçoit-elle les hauteurs ?
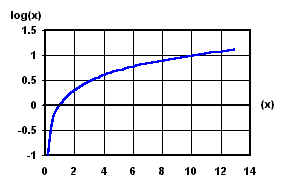
En premier, nous allons rappeler et commenter le principe de la loi de Fechner qui est la suivante : ‘la sensation varie avec le logarithme de l’excitation’. Cette loi s’applique globalement à tous nos sens. Il s’agit d’une quantité évaluée en prise directe avec notre corps et non d’une quantification arbitraire issue d’un appareil de mesure.
Rappelez- vous du profil de la courbe des ‘log’, au bout d’une certaine quantité les X peuvent beaucoup augmenter, les Y se fatiguent et n’augmentent plus que faiblement. C’est ainsi que notre cerveau réagit, il n’ajoute pas arithmétiquement les quantités, mais il les ‘compresse’. Cette notion sera très utile à rappeler lorsque nous parlerons plus tard des intensités sonores.
Mais revenons à nos hauteurs, et vous allez constater que ces deux paramètres sont étroitement liés.
Commentaires du diagramme de Fletcher
Comment a-t-on établi la courbe la plus basse appelée : seuil d’audition ?
On fait entendre à un volontaire (déontologiquement, c’est préférable !), une à une des fréquences croissantes. A chaque fréquence fixée, on part à très faible niveau sonore et l’on augmente jusqu’à ce que le sympathique volontaire perçoive le son : il s’agit bien d’un seuil déterminé à partir de la limite ‘je n’entends pas, maintenant j’entends’.
Constat : notre oreille est paresseuse dans le grave et dans l’aigu. En effet, il faut relever l’intensité dans ces deux zones pour pouvoir percevoir ces fréquences. On constate par contre qu’autour de la fréquence de 3000 Hz, il faut peu de niveau pour que l’oreille réagisse. Cette zone particulièrement performante sera appelée : zone sensible de l’oreille.
Les résultats obtenus dans l’ensemble de cette expérience varient suivant les individus, mais comportent cependant suffisamment de constantes pour être pris en considération.
Comment évalue-t-on la courbe du seuil de douleur ?
Toujours avec notre sympathique volontaire avec qui l’on réitère l’expérience, mais cette fois-ci la limite mesurée est ‘j’entends… Arrêtez, ça fait mal !’. L’on détermine ainsi la courbe supérieure, qui est celle du seuil de douleur.
Constat : moins creusée que la précédente, cette courbe oscille pour l’ensemble des fréquences, entre 110 et 130 dB.
Valeurs intermédiaires comprises entre ces deux courbes
Elles recouvrent la surface de ce que l’on appelle l’aire du champ auditif humain. Figure 3, vous sont représentées les zones de la voix parlée et de la musique.
Mais revenons en figure 2 à ces courbes. Elles se nomment des isotonies. On pourrait les appeler les ‘on croit que’. En effet si l’on suit par exemple la courbe 20 dB, notre oreille ‘croit que’ toutes les fréquences alignées sur cette courbe sont à la même intensité… Subjectivité totale si l’on compare fréquence par fréquence la valeur de l’isotonie et la valeur réelle de l’intensité sur l’axe vertical du diagramme !
Comment détermine-t-on ces courbes ?
Encore une petite expérience directe sur l’individu à qui l’on demande d’ajuster lui-même l’intensité de la fréquence entendue par rapport à un son de référence, jusqu’à ce que les deux lui ‘semblent’ être au même niveau.
Nous avons dit que ces résultats variaient suivant les individus et qui plus est, ces expériences sont faites avec à la base des sons sinusoïdaux donc simples et sans timbre.
Il est intéressant cependant d’en tirer quelques conséquences pour le musicien. À intensités égales, deux fréquences éloignées n’ont pas du tout la même chance d’être perçues de la même façon. Ces notions sont connues depuis longtemps en facture instrumentale et aussi chez les accordeurs d’instruments qui s’alignent sur la perception de la justesse évaluée par l’oreille humaine et non par le calcul uniquement mathématique des intervalles. Un piano physiquement juste ne serait pas satisfaisant dans le grave ni l’aigu !
C’est ainsi qu’a été établie une autre échelle des hauteurs : LES MELS. Ce sont en quelque sorte des ‘Hertz humains’ tenant compte de la déviation de la courbe de réponse de notre oreille. Cette échelle est à considérer avec toute la subjectivité liée à son principe d’évaluation, mais donne un profil représentatif du phénomène. Ainsi, autour de la zone sensible de l’oreille, les Hertz et les Mels s’accordent encore, mais par exemple dans l’aigu, rien ne va plus, car à 5000 Hertz ne correspondent que 4000 Mels ! Notre oreille perçoit cette fréquence en dessous de sa valeur physique réelle.
La bande passante
Tout comme nous avons pu définir des limites fonctionnelles pour l’oreille, on peut vérifier que l’utilisation des appareils de traitement sonore est aussi régie par de telles contraintes. Celles-ci seront en revanche, purement mécaniques ou électroniques, et ne laisseront évidemment que peu de place à une dimension psychologique ou subjective. En effet, avez-vous remarqué comme dans certains cas, on est tout à fait capable de complètement censurer intellectuellement un signal pourtant parfaitement audible ? Les riverains d’une autoroute ou d’une voie de chemin de fer sauront de quoi nous parlons ! Nos appareils de mesure, de captation, de stockage ou de restitution seront eux, parfaitement incapables de faire la part des choses et traiteront le moindre des signaux qu’ils perçoivent…
|
|
La notion de ‘bande passante’ est une donnée importante des caractéristiques d’un appareil. Elle précise le domaine fréquentiel qu’il sera capable de traiter, en indiquant la ‘largeur’ de la bande de fréquences gérée. Dans l’absolu, elle concerne davantage les instruments acoustiques, en lien à la fois avec leur tessiture et les caractéristiques du résonateur, qui ne changent pas. Pour les équipements électriques, il sera judicieux de compléter cette notion de celle de ‘courbe de réponse’ qui définit le niveau ‘nominal’ de fonctionnement de l’appareil, à l’intérieur de la bande passante. Cette analyse est fondamentale lorsque l’on parle d’un transducteur, à savoir un microphone ou un haut-parleur, mais elle a également toute sa valeur en ce qui concerne les outils de traitement. Tout comme on a pu le constater avec le diagramme de Fletcher à propos de notre oreille, un équipement n’aura que rarement une courbe de réponse parfaitement plane ; cela ne simplifiera pas notre tâche : le capteur n’est pas parfaitement homogène, le traitement non plus et notre oreille fait… ce qu’elle peut ! De quoi avoir quelques réserves sur la notion de ‘perfection’ ou ‘d’excellence’ sonore à la fin ! La bande passante est la largeur, mesurée en Hertz, d’une plage de fréquences f2 – f1 comprise entre les deux limites théoriques de captation auditive.
Avec les équipements analogiques, il est assez facile d’évaluer la courbe de réponse : c’est une tension électrique dont on peut aisément mesurer les déviations au fur et à mesure de l’évolution dans le spectre de fréquences. En numérique, où le signal est stocké de manière discontinue, c’est chaque échantillon qui en construit l’identité : la qualité dépend donc de la fréquence d’échantillonnage. On doit nécessairement faire appel à un convertisseur qui va transformer les données analogiques en données chiffrées. Selon le principe énoncé par le théorème de Shannon, on sait que pour qu’un échantillonnage soit suffisamment représentatif, la fréquence de mesure doit être au moins le double de celle du signal échantillonné. Si l’on se rapporte à nouveau aux limites physiologiques de perception de l’oreille, il nous faut donc analyser le signal à une fréquence supérieure à 40kHz. Le CD a choisi 44,1kHz, le DAT et de nombreux supports numériques ont adopté 48kHz. Et… on trouve maintenant fréquemment des échantillonnages à 96kHz, et même parfois plus… On peut donc raisonnablement se demander si, hormis la ‘course aux armements’ que se font les constructeurs, cela présente un véritable intérêt pour l’utilisateur ; en augmentant la fréquence d’échantillonnage, on réduit la discontinuité du signal et on augmente le rapport signal/bruit.
Deux éléments indissociables de la bande passante
Il est en effet difficile d’aborder la notion de courbe de réponse sans évoquer deux mesures complémentaires : le niveau de bruit de fond et le rapport signal/bruit.
Le bruit de fond
|
|
Toute machine, électrique, électronique, informatique génère lorsqu’elle est alimentée, un bruit de fond lié à son fonctionnement. La mesure de bruit de fond tout comme celle du rapport signal/bruit sera souvent bien plus parlante que la courbe de réponse… Le bruit de fond est mesuré en dBm. Avec les appareils numériques, c’est précisément à ce niveau, en choisissant des convertisseurs plus ou moins bon marché, qu’un fabricant pourra réaliser des prix d’appels attractifs : tout porte à croire qu’un lecteur CD à 50€ sera moins performant qu’un autre à 400€… Ce ne sera pas tant au niveau de la courbe de réponse que du niveau de bruit qu’il faudra chercher les différences. Plus ce niveau est faible, meilleure est évidemment la qualité de l’appareil et il doit se trouver à un niveau bien inférieur à celui du signal utile. L’un des grands avantages du traitement numérique du signal audio a été de permettre de dissocier le bruit de fond inhérent à la bande magnétique par exemple, du signal analogique qui une fois codé, s’exprime en données chiffrées insensibles au bruit. C’est ce qui a, en son temps, fait le succès du DAT, de l’ADAT et des ‘gros’ enregistreurs numériques à bandes tels les 3324 ou 3348 Sony.
Le rapport signal/bruit
Ce rapport découle directement de ce que nous venons d’aborder dans nos deux précédents paragraphes : le rapport signal/bruit (Noise to Signal Ratio, N/S) s’exprime comme étant le rapport entre le niveau nominal tel que nous l’avons décrit plus haut et le niveau de bruit de fond. Plus ce rapport sera élevé, meilleure sera la qualité de l’appareil. Si un appareil a un niveau nominal de +10dBm, et un niveau de bruit mesuré à –60dBm, on disposera donc d’un rapport signal/bruit de 70dBm. Si l’on tient compte de la réserve (headroom) prévue par le constructeur entre le niveau nominal et le niveau maximal, on pourra atteindre environ 80dBm.

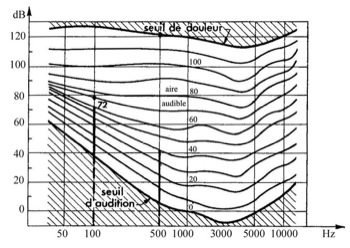
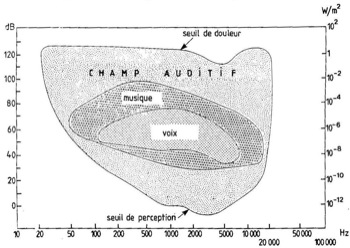
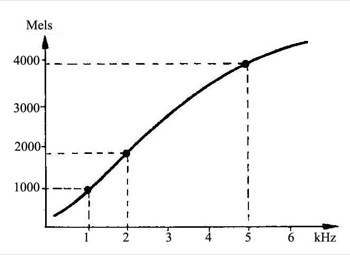
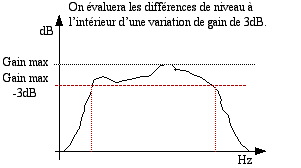 Fig.5
Fig.5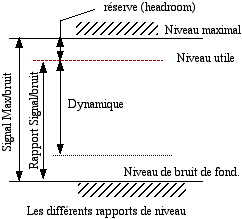 Fig.6
Fig.6