SONDAGE : y a-t-il quelqu'un qui puisse distinguer 44.1 vs 48 khz en test "à l'aveugle" ?

Citation :

 

Plutôt que de se focaliser sur la fréquence d'échantillonnage, il vaut mieux regarder la plage dynamique, le taux de distorsion et le rapport signal bruit.  Cela sera plus parlant en termes de qualité que la fréquence d'échantillonnage

 

 oui mais tout ca est lié, changer la FE influe sur le SNR et le THD (et pas en bien)

Citation :

Par exemple tu m'expliquera comment on effectue une division binaire (ou numérique, globalement) sans perte d'information

 faudrait que je refasse le test parce que sur le coup j'ai un doute sur le résultat, mais il me semble que c'est simple à démontrer:

prendre une piste audio 24 bit, appliquer une atténuation de x dB, puis en série un gain de la même valeur, exporter en 24 bit et comparer l'export avec la piste originale, de mémoire ca s'annule parfaitement, donc pas de pertes, à moins comme expliqué dans la doc du mixer TDM de PTHD de tomber pil poil sur un multiple de 6.02xxxxxxxxxxxxx (+ l'infini derrière la virgule)

sinon pour répondre à la question de base, je suis incappable de distinguer les deux, et j'avais même fait le test d'un mix complet en 44.1 et le même en 88.2 ( devias bien y avoir une cinquantaine de pistes) et j'entendais toujours aucune différence sur un système de monitoring plutôt correct.

Citation de : scare

Citation :

en 48khz, il y a plus de "points" d'échantillonnage qu'à 44.1... est-ce possible de différencier cela à l'oreille ?

Aie aie aie 

Le son que tu entend au travers de tes enceintes n'est pas un son échantillonné mais un son reconstruit via un CNA : ce son est bien analogique.

Du moment que tu respectes le théorème de Shanon-Nyquist indiquant que la Freq d'echantillonnage est strictement supérieure à deux fois la bande passante, ton signal sera théoriquement parfaitement reconstruit.

Oui c'est bon, je sais bien que le son est converti en analo avant d'aller sur mes enceintes, merci ! Donc tes "aie aie aie " , merci bien.

Citation de scare :

 

 

Le signal audio ayant une bande passante de 20 kHz, une Fe de 44,1 kHz suffit donc à reconstruire "parfaitement" le signal.

Le fait d'être en 48 kHz ou 96 kHz, donc d'avoir plus de point d'échantillonnage n'apportera rien de plus pour le reconstruire.

Non c'est faux.

Imaginons qu'on ait une sinusoïde de 10 000hz.  A 44.1khz,  on disposera exactement, en moyenne, de 4,1 "points d'échantillonnage" par période de sinusoïde (dans le signal discrétisé).
Si le converto numérique->analo   ne "lisse pas" la courbe,   ça donnera une sinusoïde reconstituée à partir de 4 segments de droite par période,    c'est à dire *pas du tout* une belle sinusoïde.

Au contraire, en 96 khz, chaque période de cette sinusoïde 10 000hz sera représentée par 9.6 points de discrétisation. Ce qui amènera une meilleure "reconstitution" de la sinusoïde en question.

Moralité : même pour un signal de 10 000hz (en dessous de la fréquence limite de Shanon Nyquist),   un échantillonnage à 96khz  est meilleur qu'en 44.1 khz   (ce qui parait logique d'ailleurs).

[ Attention : j'ai jamais dit qu'en pratique quelqu'un pouvait faire la différence entre les deux !! ]
C'était juste pour dire que, scare, tu fais dire au théorème de Shanon-Nyquist ce qu'il ne dit pas.

A+ Jebb

On peut faire des division, tu peux en faire ici si tu veux !

Après je ne vais pas partir dans la division de 4233,6 / 96 pour te faire plaisir hein !!

Aprés elle ne tombent pas toutes justes, comme en décimal.

Aussi les valeurs 44,1  ou 96 ou 4233,6 étant parfaitement codable en binaire, sans arrondi, je ne vois pas pourquoi ce serait impossible.

Citation :

 

Je viens de comparer les données techniques entre un convertisseur haut de gamme en 44.1 et un autre en 192 kHz qui se situe dans l'entrée du "moyen de gamme" et est très utilisé en home studio.

Rien que pour la dynamique, en A/N on obtient 121 dB (en 44.1) chez l'un et 105 dB (en 192 kHz) chez l'autre.

Il est très probable que dans ce cas précis, le 192 kHz rendra...moins bien que le 44.1 kHz.  Plutôt que de se focaliser sur la fréquence d'échantillonnage, il vaut mieux regarder la plage dynamique, le taux de distorsion et le rapport signal bruit.  Cela sera plus parlant en termes de qualité que la fréquence d'échantillonnage.

 

 

C'est là ou l'électronique rentre en jeu. C'est l'electronique qui fera les différences de son. De là a établir des règles, ça me parait compliqué, ça dépend du fonctionnement du convertisseur.

Alors en fait pour passer de 96 à 44.1, tu dis qu'il faut passer par un upsampling pour arriver à la fréquence de 4233,6 Hz.

Je traduis dans l'espace des temps tu as 96 000 échantillons à la seconde, pour n'en déduire que 44 100, tu va extrapoler 4233 600 échantillons à partir de tes 96 000, par une interpolation. l'interpolation c'est une moyenne pondérée, tu additionne des échantillons (c'est les échantillons de son du départ, ils peuvent prendre n'importe quelle valeur par définitions), que tu as divisé par un coefficient de pondération. Cette division amène une perte d'information. Une fois cette interpolation faite on peut downsampler à 44.1 kHz d'accord.

Docks => Dans ton exemple tu pars de 24 bits que tu atténue, donc tu supprime les bits de poids faible, quand tu amplifie, comment ton système recrée les bits qui ont disparu ? Si tu sais comment, pourquoi stocker la donnée en 24 bits, vu qu'il est possible d'en utiliser moins et de réinventer les maquant ?

Edit : rroland : certe

Citation de : jebb6667

Non c'est faux.

Imaginons qu'on ait une sinusoïde de 10 000hz.  A 44.1khz,  on disposera exactement, en moyenne, de 4,1 "points d'échantillonnage" par période de sinusoïde (dans le signal discrétisé).
Si le converto numérique->analo   ne "lisse pas" la courbe,   ça donnera une sinusoïde reconstituée à partir de 4 segments de droite par période,    c'est à dire *pas du tout* une belle sinusoïde.

Au contraire, en 96 khz, chaque période de cette sinusoïde 10 000hz sera représentée par 9.6 points de discrétisation. Ce qui amènera une meilleure "reconstitution" de la sinusoïde en question.

Moralité : même pour un signal de 10 000hz (en dessous de la fréquence limite de Shanon Nyquist),   un échantillonnage à 96khz  est meilleur qu'en 44.1 khz   (ce qui parait logique d'ailleurs).

Desole mais c'est toi qui a tort, le theoreme de Shanon et Nyquist ne se resume pas a : "si j'ai au moins 1 point par demie periode, c'est suffisant". (niveau bac L)

Il est beaucoup plus complexe que ca, et montre que l'on peut reproduire une courbe parfaitement lisse et identique avec fs>=fe/2.

Citation :

Imaginons qu'on ait une sinusoïde de 10 000hz.  A 44.1khz,  on disposera exactement, en moyenne, de 4,1 "points d'échantillonnage" par période de sinusoïde (dans le signal discrétisé).
Si le converto numérique->analo   ne "lisse pas" la courbe,   ça donnera une sinusoïde reconstituée à partir de 4 segments de droite par période,    c'est à dire *pas du tout* une belle sinusoïde.

En fait on s'en fout complètement du nombre de point par période. Ce qu'il faut c'est au moins plus que 2/période, sinon arrive le phénomène d'aliasing.

A 22049Hz on en a 2,00009 points par période et on reconstitue parfaitement la sinusoïde.

Un CNA intègre toujours un filtre passe bas qui lisse le signal, c'est justement ça sa fonction 

Lorsque tu échantillonnes, le spectre du signal de départ est répliqué à tout les multiples de Fe : 0, Fe , 2*Fe, 3*Fe, etc etc.

Il suffit donc de placer un filtre passe bas de fréquence de coupure la bande passante du signal pour retrouver ta sinusoïde d'origine.

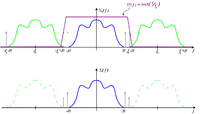
Ci-dessous le filtre passe bas appliqué sur un signal échantillonné :

Voici une illustration à 10 kHz :

En haut le signal à 10 kHz discrétisé (les points sont reliés mais c'est schématique en réalité ils de sont pas reliés), en bas le signal reconstruit parfaitement.

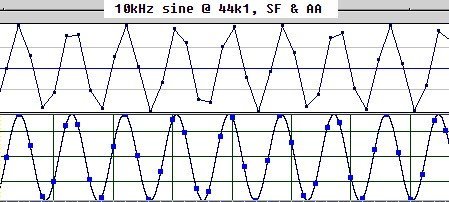
Sache aussi que si tu prends une freq de 22049, avec une Fe de 44.1, tu n'auras que 2, 00009 point par période et la sinusoïde sera parfaitement reconstruite (en considérant le passe bas en brick wall parfait).

Voilà.

Citation :

Desole mais c'est toi qui a tort, le theoreme de Shanon et Nyquist ne se resume pas a : "si j'ai au moins 1 point par demie periode, c'est suffisant". (niveau bac L)

Il pourrait se résumer à "au moins plus que deux points par période". c'est équivalent à Fe > 2 * BPsignal

Citation de : jeriqo

Desole mais c'est toi qui a tort, le theoreme de Shanon et Nyquist ne se resume pas a : "si j'ai au moins 1 point par demie periode, c'est suffisant". (niveau bac L)

Il est beaucoup plus complexe que ca, et montre que l'on peut reproduire une courbe parfaitement lisse et identique avec fs>=fe/2.

Peut tu expliquer ce que tu avances ou donner une référence ?

Je maintiens qu'échantillonner un signal périodique avec 9 points par période est forcément plus précis qu'un échantillonnage à 4 points par période.  Tout simplement parce que

{ l'ensemble des signaux f   t.q. f(a_1)=x_1, ..., f(a_9)=x_9} est strictement inclus dans

{ l'ensemble des signaux f    t.q.  f(a_1)=x_1, ..., f(a_4) = x_4}.

Prouve moi le contraire si tu veux ;)

jebb6667, le post de scare est clair la dessus, oui tu as plus d'information pour reconstruire le signal, mais encore une fois 2 points par période c'est suffisant, plus, c'est de la redondance d'informations (information inutile pour reconstituer le signal analogique, mais utile quand on fait dans ce cas des traitements temporels, qui risque de faire perdre de l'information donc on en prends plus pour avoir de la marge=> d'où le 96 kHz).

Jebb6667, sans animosité, il faut que tu te procures un cours sur l'échantillonnage. Car là c'est la base.

Je vais essayer de t'en trouver un.

On n'est plus dans "prouve moi si ou ça", c'est un théorème fondamental en audio, et tu va fatiguer tout le monde

Tant que Fe > 2 *BandePassante tu reconstruis parfaitement ton signal, ok ?

Le cours arrive

Citation :

Dans ton exemple tu pars de 24 bits que tu atténue, donc tu supprime les bits de poids faible, quand tu amplifie, comment ton système recrée les bits qui ont disparu ?

 tu supprimes rien, les calculs sont fait en flottant de manière général, encor une fois faut que je refasse le test pour affirmer pleinement ce que j'avance, mais de mémoire je retrouvais bien mes petits.

Pour le coup du nombre de point, je crois que tout simplement (si j'ai bien compris Nyquist) à partir d'un minimum (strictement > Fe/2), y'a pas 36 sinusoïdes qui passent par tes points, t'auras beau en ajouter 250 si tu veux, ca changera rien qu'avec le minimum requis tu peux parfaitement recréer la sinusoïde et que ca sera la même, avec 10 points ou 250, ce que montre très bien le schéma de scare.

Docks => logiquement tu dois pouvoir faire le test en baissant le volume d'un tiers (un cinquième ou un septième etc...) et en le remettant à 100% ensuite, logiquement tu devrait avoir des différences, même en flottant.

http://physiquemangin.pagesperso-orange.fr/BTSSE/cours/echantillonnage.pdf

Ok je veux bien un lien vers un cours.

NOn il n'y a aucune animosité dans mon post non plus ;)

Ce que tu expliques, quand tu dis "reconstruire parfaitement le signal", c'est qu'il existe une et une seule sinusoïde de fréquence <=22050hz qui passe par f(a_1) = x_1   et f(a_2) = x_2      (si a_1 et a_2 sont 2 points consécutifs d'un échantillonnage à 44.1khz) ? c'est bien ça ?

Oui c'est ca.

Car quand tu raisonnes en fréquentiel (je pense que c'est ca qui te manque), le spectre de la sinusoide est toujours la, même si tu n'as plus que 2,0000000000001 point.

le passe bande sert à récupérer ce spectre... et la hop magie, la sinusoide réapparait dans les enceintes.

C'est fascinant ! Et c'est pas le plus grand cabaret du monde !

Citation :

raies à 21.5k et 22.6k

Pourquoi t'obtiens deux raies  et pas une raie à 21,5 ?  

La deuxième raie c'est la différence entre la réalité et la théorie, les filtres ne sont pas parfait, donc on "voit" l'image du spectre qui commence à être répété.

Danguit,

Citation :

Même manip en 96k sur US-2000 et UA-4FX => la fréquence image (26.5k) n’est plus visible (elle est trop faible) et le Softclipper n’a plus d’effet, ni à l’œil ni à l’oreille.

Pq 26,5 ?

Dans le premier test tu reconstruis à partir de 44,1 et rééchantillone à 48 Khz

Et dans le deuxième tu passes de 96 à 96 ?

T'as gagné je comprends plus rien de ce que tu as fais  (en même temps j'arrive de Nouméa avec 30 h de vols + 18 h que je suis debout, carbonisé  )

J'essaye de la refaire :

1)Tu génères un sinus 21,5 kHz avec une Fe à 44,1 kHz

2)Tu la sors sur la sortie d’une carte US-2000 Tascam et la réenregistre en 48 Khz via une UA-4FX

3) tu observes des raies à 21.5k et 22.6k (image par rapport à 22.05k) à # -10dB

ensuite

1)Tu génères un sinus 21,5 kHz avec une Fe à 96 kHz

2)Tu la sors sur la sortie d’une carte US-2000 Tascam et la réenregistre en 96 Khz via une UA-4FX

3) tu observes une raie à 21.5k

J'ai bon ?

J'ai une question par curiosité concernant le test à 44,1 kHz est ce que tu pourrais faire la chose suivante :

1)Tu génères un sinus 21,5 kHz avec une Fe à 44,1 kHz

2)Tu le sors sur la sortie d’une carte US-2000 Tascam et la réenregistre en 44,1 Khz via une UA-4FX

3)Tu me dit si tu observe encore les deux raies.

Je voudrais savoir comment se comporte le filtre anti aliasing en entrée du CAN à 44,1 Khz

Est-il plus sélectif ?

2eme question, est que tu pourrais me dire quelle puce CAN et CNA équipe ta carte UA-4FX

3eme question, est-il possible de refaire le 1er test que tu as fait en inversant les deux cartes.