SONDAGE : y a-t-il quelqu'un qui puisse distinguer 44.1 vs 48 khz en test "à l'aveugle" ?
- 115 réponses
- 19 participants
- 35 988 vues
- 16 followers
Anonyme
Je cherche à voir vraiment la différence de qualité entre les deux.
Je connais bien les arguments théoriques (-> théorème de shanon qui dit qu'en 44.1, la fréq maximale est 22050 hz , en 48khz, la fréq max est 24000 hz, etc.),
mais je voulais savoir si "en pratique", un auditeur à l'oreille très fine peut-il distinguer les 2 (sur un son monophonique enregistré avec du très bon matos micro, préamp, convertisseurs).
QUelqu'un ici saurait-il distinguer les 2 ?
A+ Jebb
[ Dernière édition du message le 22/11/2010 à 16:50:38 ]
scare
Putain ! la fréquence disparait, c'est grace au suréchantillonnage du Delta Sigma Whaouuuu !!
Cela équivaux à un filtre anti-aliasing avec une pente ultra raide. ![]()
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Tonka
Peut-être un peu hors sujet, mais pour compléter ou expliquer différemment l'explication de Scare, je préciserais plutôt les choses comme ça :
On enregistre en général un signal musical, pas une sinusoïde pure... donc on a un son qui se compose d'harmoniques de fréquences de plus en plus élevées dont la somme crée un signal complexe présentant des détails visibles sur la forme d'onde. C'est ce que nous dit l'analyse de Fourrier.
Il est évident comme le pressent Jebb que si la fréquence d'échantillonnage est plus élevée, on percevra des détails qui ne seront pas enregistrés à une fréquence d'échantillonnage plus basse. Lorsqu'on reconstituera le signal au final, on ne pourra pas recréer par lissage une information non enregistrée. Donc effectivement la courbe recréée à partir de la Fe la plus basse sera moins détaillée, c'est parfaitement logique.
SAUF QUE...
ces petits détails par lesquelles les deux courbes diffèreront, correspondront, dans une analyse de fourrier, à des harmoniques de fréquences supérieures à 2x la Fe la plus basse donc entre 22,2 et 24 kHz dans le cas qui nous intéresse... Donc des fréquences à priori inaudibles pour nous...
Ou pour présenter les choses d'une manière encore différente: quand on enregistre un son de fréquence proche de 20 kHz, avec une Fe de 44,1 kHz, on n'enregistre que sa fondamentale... mais ses harmoniques sont de toute façon inaudibles, donc on perd rien....
Danguit
Je peux me tromper mais je tire de mes petits essais informels l'impression que l'entrée des cartes son est mieux soignée que la sortie (filtres anti-repliement d'un côté, reconstruction de l'autre). Serait-ce corrélé au fait que chacun peut facilement contrôler le signal numérisé (analyseurs divers et variés) alors que (presque) personne ne vérifie le signal analogique en sortie ?
scare
Citation :
Il est évident comme le pressent Jebb que si la fréquence d'échantillonnage est plus élevée, on percevra des détails qui ne seront pas enregistrés à une fréquence d'échantillonnage plus basse. Lorsqu'on reconstituera le signal au final, on ne pourra pas recréer par lissage une information non enregistrée. Donc effectivement la courbe recréée à partir de la Fe la plus basse sera moins détaillée, c'est parfaitement logique.
Et moi je te dirais qu'aujourd'hui on échantillonne à 6,144 Mhz à peu prés. Et ensuite on décime à la fréquence voulue.
Citation :
ces petits détails par lesquelles les deux courbes diffèreront, correspondront, dans une analyse de fourrier, à des harmoniques de fréquences supérieures à 2x la Fe la plus basse donc entre 22,2 et 24 kHz dans le cas qui nous intéresse... Donc des fréquences à priori inaudibles pour nous...
2x la fe la plus basse ? donc 88,2 kHz ? 
non seulement elles sont inaudibles mais la plupart des micros ou preamp vont fortement les réduire.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Dr Pouet
mais je voulais savoir si "en pratique", un auditeur à l'oreille très fine peut-il distinguer les 2 (sur un son monophonique enregistré avec du très bon matos micro, préamp, convertisseurs). Quelqu'un ici saurait-il distinguer les 2 ?
Même si une fréquence d'échantillonnage plus élevée entrainait une meilleure définition, ces 2 fréquences sont très proches... en fait le 44kHz est pour le CD et le 48 pour la vidéo. Règle simple : il vaut mieux travailler à la fréquence de destination. Ou au double.
Point important :
(ça pourrait être une conclusion de l'autre débat) on fait souvent une analogie entre résolution en pixel pour une image et fréquence d'échantillonnage. Bien que ça semble de bon sens, c'est infondé. Une meilleure analogie serait : "pour mesurer des trucs avec un pied à coulisse, vaut-il mieux faire 2 fois plus de mesures, en prenant 2 fois moins de temps et en lissant à la fin, ou pas ?"
On comprend qu'en mesurant 2 fois plus vite, cette mesure est moins précise. C'est exactement ce qui se passe en électronique. D'où la conclusion simple: il est faux de dire que 44kHz < 88kHz et 88 < 176 ; en pratique c'est plus compliqué que ça. La preuve en chiffres, dans l'exemple donné par RRoland.
Bon là on parle de conversion numérique -> analogique et réciproquement. Après, dans le séquenceur, on peut travailler à une autre fréquence.
Pour les synthés et pour éviter l'aliasing, vaut mieux être à 88 qu'à 44 (mais si le synthé fait déjà de l'upsampling en interne, ça ne va rien changer). Si on fait pas mal de pitch-shifting ou de time-scaling, il parait que c'est mieux aussi d'être à 88, et ça ne semble pas illogique. A l'inverse, si on utilise Live, il est établi qu'il faut désactiver ces fonctions quand on n'en a pas besoin, car sinon c'est sûr que l'on perd beaucoup ! (plus qu'en prenant une FE pas idéale)
la bonne blague c'est que justement a la base il me semble que le 44.1 était un standard vidéo
Je crois que tu confonds avec le fait que cette fréquence précise a été choisie parce-que techniquement les données étaient faciles à stocker sur des cassettes vidéo (en numérique, et à la place des données vidéo) ; mais rien à voir avec la fréquence d'échantillonnage du son pour de la vidéo :
U-matic would also see use for the storage of digital audio data. Most digital audio recordings from the 1980s were digitally mastered to U-matic tape. The Sony PCM-1600 PCM adaptor used a U-matic recorder as a transport. The PCM-1600 output standard "pseudo video" in 525/60 format, which appeared to be a video image of vibrating checkerboard patterns that could be recorded on a video recorder. The PCM-1600 was the first system used for mastering audio compact discs in the early 1980s, with the famous Compact Disc 44.1 kHz sampling rate based on a best-fit calculation for the U-matic's video horizontal-sync rate. The later PCM-1610 and 1630 units also used U-matic cassettes as a storage medium.
Sur 6 milliards d'être humains, il n'est pas impossible que 4 ou 6 personnes entendent jusqu'à 25 khz. Il existe des anormalités biologiques, c'est certain. En revanche, pour un quidam, impossible.
Oui. C'est pas pour rien que depuis des années on considère qu'en hifi c'est 20hZ - 20kHz.
Faites l'essai de supprimer ce qui est au-delà de 19kHz et voyez si ça vous gêne beaucoup.
Au-delà de 25 / 30 ans, c'est peu probable...
[ Dernière édition du message le 23/11/2010 à 21:09:55 ]
scare
Citation :
Je peux me tromper mais je tire de mes petits essais informels l'impression que l'entrée des cartes son est mieux soignée que la sortie (filtres anti-repliement d'un côté, reconstruction de l'autre). Serait-ce corrélé au fait que chacun peut facilement contrôler le signal numérisé (analyseurs divers et variés) alors que (presque) personne ne vérifie le signal analogique en sortie ?
Perso je suis en phase d'apprentissage sur le converto, je commence à être pas mal au point sur le CAN, juste encore un poil la décimation avec les Sinc3 et half band à potasser.
Mais ce qui est sûr c'est que le fait d'échantillonner à plusieurs MHz implique que le filtre analo d'entrée n'a pas besoin d'être raide pour atténuer suffisement avant d'atteindre Fe/2
Par exemple échantillonnage à 6,144 MHz, ca donne Fe/2 à 3,072 MHz
Le filtre passe bas d'entrée tu le mets à 360 Khz comme ca il est parfaitement flat de 0 à 30 Khz, pas de ripple, le rebond à la freq de coupure n'est pas dans la BP audio.
C'est un filtre du 1er ordre, pas besoin d'un filtre complexe, ça fait - 20 dB / decade , c'est à dire qu'on est à - 20 dB à 3,6 Mhz.
Or on utilise la technologie delta sigma, sur 1 bit, dont la bande passante à un RSB de 6,02 + 1,76 dB = 7,78 dB
Donc rien qu'avec le filtre analo on est déjà parfait (-20 dB comparé au 7,78 db de RSB)
On comprend déjà tout l'intérêt de ce type de converto.
Aucun aliasing possible.
Ensuite l'ordre du modulateur delta sigma permet de faire du noise shaping et d'améliorer le RSB jusqu'à atteindre les 24 bits.
pour terminer le couple filtre passe bas digital + décimation, dont la pente est clairement très très raide, permet de couper parfaitement à 22,05 KHz par exemple.
C'est pour ça que ta raie disparait quand tu enregistre à 44,1 kHz
Après concernant le CNA, j'y suis pas encore, je serais précis dessus dans quelques temps.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 23/11/2010 à 21:07:42 ]
Dr Pouet
Ce que tu expliques, quand tu dis "reconstruire parfaitement le signal", c'est qu'il existe une et une seule sinusoïde de fréquence <=22050hz qui passe par f(a_1) = x_1 et f(a_2) = x_2 (si a_1 et a_2 sont 2 points consécutifs d'un échantillonnage à 44.1khz) ? c'est bien ça ?
C'est bien ça.
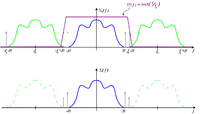
J'en profite pour rentabiliser l'image que j'avais faite

(cliquer pour agrandir)
- les pointillés bleus sont les instants d'échantillonnage
- les losanges sont les valeurs des samples
Que peut-on faire passer par ces samples ?
- la sinusoïde rouge, d'amplitude max, et de fréquence Fe
- pas la verte, de même fréquence, mais d'amplitude inférieure
- pas la jaune ni la bleue, dont les fréquences sont trop basses pour passer par tous les points.
- pas de forme d'onde différente de la sinusoïde, car une telle forme contiendrait des harmoniques plus élevées (F 3F 4F...), lesquelles seraient de fréquence plus élevées que Fe/2, donc virées par le filtrage, qui ne laisserait que la fondamentale, sinusoïdale.
Imaginons qu'on ait une sinusoïde de 10 000hz. A 44.1khz, on disposera exactement, en moyenne, de 4,1 "points d'échantillonnage" par période de sinusoïde (dans le signal discrétisé). Si le converto numérique->analo ne "lisse pas" la courbe, ça donnera une sinusoïde reconstituée à partir de 4 segments de droite par période, c'est à dire *pas du tout* une belle sinusoïde.
L'hypothèse "ne lisse pas la courbe" n'est pas compatible avec le théorème de Nyquist/Shannon. En effet, sans lissage ça fait des fréquences nettement supérieures à Fe/2...
Tonka
Hors sujet :
effecticement dans ma contrib il fallait lire que les détails qui diffèreront correspondront à des fréquences supérieures à la moitié (et non 2x) la Fe la plus basse, donc entre 22,1 et 24 kHz
stipe60
Citation de : stipe60
La deuxième raie c'est la différence entre la réalité et la théorie, les filtres ne sont pas parfait, donc on "voit" l'image du spectre qui commence à être répété.
Bon l'image n'est pas très lisible...
je vais essayer de détailler un peu suite à une demande en MP (lucas, si tu nous lis... ![]() ) En fait le signal en bleu c'est le signal audio que l'on souhaite échantillonner, l'axe vertical au milieu c'est la fréquence '0' et plus on s'éloigne, plu on augmente la fréquence, le trait violet représente le filtre, il est haut autour de '0', donc dans les basses fréquences jusqu’à 20 kHz environ, et descends raide pour couper le signal.
) En fait le signal en bleu c'est le signal audio que l'on souhaite échantillonner, l'axe vertical au milieu c'est la fréquence '0' et plus on s'éloigne, plu on augmente la fréquence, le trait violet représente le filtre, il est haut autour de '0', donc dans les basses fréquences jusqu’à 20 kHz environ, et descends raide pour couper le signal.
Ce qu'on voit en vert, c'est un artéfact / défaut du à l’échantillonnage (l'histoire de shanon), c'est un peu trop ancien pour que je l'explique comme ça avec les mains, si quelqu'un est tenté ![]() ... pour résumer on voit bien que le signal échantillonné de 0 à 22,05 kHz est répété en miroir de façon périodique centre sur différentes fréquences. Les flèches c'est le signal qu'a créé danguit (21,5kHz), comme le filtre n'est pas en forme de rectangle parfait mais avec des bords en pente (parallélogramme) du coup la flèche qui est répétée (en miroir) n'est pas suffisamment filtrée pour disparaître donc il reste du signal à 22,05 + (22,05-21,5) = 22,6kHz aténué un peu (-10dB).
... pour résumer on voit bien que le signal échantillonné de 0 à 22,05 kHz est répété en miroir de façon périodique centre sur différentes fréquences. Les flèches c'est le signal qu'a créé danguit (21,5kHz), comme le filtre n'est pas en forme de rectangle parfait mais avec des bords en pente (parallélogramme) du coup la flèche qui est répétée (en miroir) n'est pas suffisamment filtrée pour disparaître donc il reste du signal à 22,05 + (22,05-21,5) = 22,6kHz aténué un peu (-10dB).
Voila si c'est pas assez clair ou trop faut n’hésitez pas à réagir lol
[ Dernière édition du message le 23/11/2010 à 22:02:04 ]
Danguit
C'est pour ça que ta raie disparait quand tu enregistre à 44,1 kHz
Ce n'est pas contradictoire avec ce que je dis : l'entrée est soignée parce que c'est simple à faire.
En revanche, quasiment à coup sûr bien que je n'ai pas encore fait la manip, si je rejoue ce beau signal à 44.1k et le numérise à 48k ou plus, je le retrouverai sur la sortie accompagné de l'autre raie etc, etc, ad lib.
lucasd'airy
Je ne sais si c Jebbb qui parlait d'une ''fréquence de destination'' mais le point me semble important. Le 48khz se distinguera d'autant mieux du 44.1 que les signaux auront été échantillonnés d'abord à une fréquence plus élevée.
Le monitoring permettra peut-être, selon les méthodes d'édition (pas de quantification bourrine), de se rendre compte qu'à comparer les mêmes signaux splittés subissant les mêmes opérations sur deux sessions cadencées à 48 et 44, la première pourra présenter un rendu plus fluide (grâce à la réduction subséquente de la latence).
Ensuite seulement vient l'aspect hi-fi de la comparaison -et je pense avoir sous-estimé ce poste budgétaire.
Cela n'enlève rien à l'intérêt des présentes spéculations! Merci à stipe60 de ses éclaircissements.
________
Danguit > à défaut d'une mesure, la progression entre les valeurs attachées aux deux raies a-t-elle plus dechances théoriques d'être ''polynômiale'' à 48khz qu'à 44,1, en supposant que la fréquence de destination n'a pas été convertie avant émission de la sinusoïde?
[ Dernière édition du message le 24/11/2010 à 00:06:26 ]
jeriqo
Quels sont les convertisseurs utilises dans ce test ?
C'est etonnant car ils echantillonnent pratiquement tous a des frequence de l'ordre du megahertz, il n'y a pas de probleme d'aliasing et d'ailleurs, il n'y a meme pas de filtrage analogique.
lucasd'airy
Que je sache, les convertisseurs utilisés pour observer les raies sont ceux de l'interface de Danguit. Pour la question des mhz, un post de Scare explique l'écart entre la valeur nominale/intrinsèque.
Danguit
1)Tu génères un sinus 21,5 kHz avec une Fe à 44,1 kHz
2)Tu le sors sur la sortie d’une carte US-2000 Tascam et la réenregistre en 44,1 Khz via une UA-4FX
3)Tu me dit si tu observe encore les deux raies.
Je me suis aperçu cette nuit que j'avais fait une réponse trop rapide à une question pas très pertinente (désolé) : il est évident qu'il n'y a rien au dessus de Fe/2, par conséquent la raie à 22.6 se replie à 21.5 et il est difficile de savoir qui est est qui.
J'ai donc refait une manip avec un signal à 23k et Fe à 96k, la sortie étant échantillonnée à 44.1. Et là, je trouve une jolie raie à fort niveau à 21.1 (càd 23 replié).
Conclusion, le filtre anti-repliement n'est pas d'une efficacité extraordinaire.
Edit : # -12 dB à cette fréquence.
[ Dernière édition du message le 24/11/2010 à 09:13:33 ]
scare
Hello Danguit,
La nuit porte conseil ![]() .
.
Je vais aller faire des essais avec mes convertos Lynx aujourd'hui. Quel soft utilises-tu pour voir les raies ?
Citation :
J'ai donc refait une manip avec un signal à 23k et Fe à 96k, la sortie étant échantillonnée à 44.1.
Tu es assez rapide dans les descriptions de tes protocoles de test, ce qui fait que je suis pas sûr de bien saisir ce que tu fais :
Comment échantillonnes-tu à 96 et sort à 44,1 ? Si ton projet est à 96 kHz, tu fais une conversion num-ana à 96 non ?
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
scare
Je pense avoir compris ( ![]() ):
):
Tu as généré un 23 kHz avec une Fe à 96kHz, tu l'as converti en analo. (96 pour ne pas supprimer le 23 lors de la CNA)
Ensuite tu as converti en Num ce 23 kHz avec une Fe de 44.1 kHz,
Résultat : tu constate un repliement à 21,1.
La vache le filtre est pourrave !
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 09:56:14 ]
Danguit
Quel soft utilises-tu pour voir les raies ?
Goldwave, qui ne semble pas savoir bien piloter toutes les cartes (ou alors c'est à cause de W7).
Comment échantillonnes-tu à 96 et sort à 44,1 ? Si ton projet est à 96 kHz, tu fais une conversion num-ana à 96 non ?
J'utilise la carte UA-4FX pour numériser un signal analogique, la source est à 96k uniquement pour avoir la bande permettant de passer le 23k.
EDIT : j'arrive trop tard !
[ Dernière édition du message le 24/11/2010 à 09:50:06 ]
scare
C'est bon mon post 66 ?
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 09:58:21 ]
scare
Sur Logic, l'oscillateur s'arrête à 20 kHz .... il faut que j'en trouve un pour aller au delà
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Danguit
En ce qui concerne les filtres, j'ai observé à peu près les mêmes comportements avec les chips son de divers PCs.
Je serais donc intéressé par des résultats sur du matériel haut de gamme pour savoir si mon matériel est vraiment pourri ou si tout le monde est plus ou moins logé à la même enseigne.
Il ne faut quand même pas oublier que l'essai est sévère : le 44.1k est prévu pour 20k max et un niveau relativement faible, alors que j'injecte un niveau élevé à une fréquence supérieure.
Edit :
Sur Logic, l'oscillateur s'arrête à 20 kHz
Idem sur cubase, c'est pour cela que je passe par goldwave ou un scope USB (moins précis).
[ Dernière édition du message le 24/11/2010 à 10:10:01 ]
Dr Pouet
Et puis vous devriez aussi tester vos oreilles (est-ce que j'entends le 19kHz, le 18kHz, le 17kHz... ?), il y a moyen d'être surpris...
scare
Oui l'essai est sévère, mais si on synthétise,
1) On peut penser qu'avec une Fe à 44,1 kHz, tous les sons proches de 20 kHz, vont générer des répliques à entre 24,1 kHz et plus.
On va peut être pas les entendre, mais c'est pas hyper carré comme fonctionnement !!
2) De même lors d'une conversion Analo-Num à une Fe = 44,1 kHz, toutes fréquences au dessus de 24,1 vont être repliées dans le spectre audio !! car le filtre anti- repliement n'est pas assez sélectif. Là c'est moins sympa.
Reste à voir si un converto "Haut de gamme" à le même comportement. Je vais faire l'essai si je trouve un générateur.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 10:19:56 ]
Dr Pouet
Pour le repliement je suis d'accord, ça semble pas terrible.
Sur Logic, l'oscillateur s'arrête à 20 kHz .... il faut que j'en trouve un pour aller au delà
Peut-être en choisissant un signal carré pour avoir des harmoniques supérieures ?
Danguit
On va peut être pas les entendre, mais c'est pas hyper carré comme fonctionnement !!
Ma remarque sur les oreilles est plutôt en rapport avec le sujet à l'origine du thread.
C'est pour cette raison que j'ai créé une non-linéarité qui, elle, peut ramener des signaux inaudibles pour le commun des mortels (ici 21.5k et 22.6k) à des valeurs audibles par tous (ici 1.1k). Cela correspond bien au phénomène décrit par J. Dunn !
scare
Danguit, pourquoi celle ci se produit elle à 1,1 kHz ?
J'ai bien compris que c'est la différence des deux raies, mais pq ça ?
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
- < Liste des sujets
- Charte