SONDAGE : y a-t-il quelqu'un qui puisse distinguer 44.1 vs 48 khz en test "à l'aveugle" ?
- 115 réponses
- 19 participants
- 35 983 vues
- 16 followers
Anonyme
Je cherche à voir vraiment la différence de qualité entre les deux.
Je connais bien les arguments théoriques (-> théorème de shanon qui dit qu'en 44.1, la fréq maximale est 22050 hz , en 48khz, la fréq max est 24000 hz, etc.),
mais je voulais savoir si "en pratique", un auditeur à l'oreille très fine peut-il distinguer les 2 (sur un son monophonique enregistré avec du très bon matos micro, préamp, convertisseurs).
QUelqu'un ici saurait-il distinguer les 2 ?
A+ Jebb
[ Dernière édition du message le 22/11/2010 à 16:50:38 ]
scare
La ligne pointillée montre le niveau de la bande repliée.
A 48 kHz,
Dans cet exemple, l'effet direct de la mauvaise réjection des fréquences dans la zone de transition serait audible pour ceux qui peuvent entendre au dessus de 18kHz.
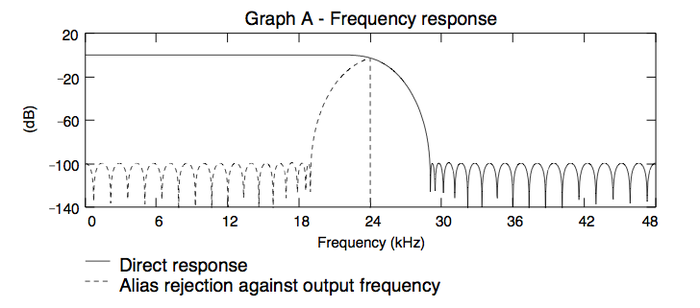
A 96 kHz, La zone repliée reste au dessus de la bande passante audio
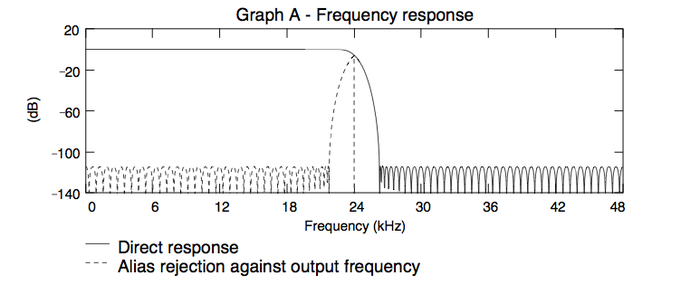
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 11:21:37 ]
Danguit
jeriqo
Juste a titre informatif, les convertisseur dont j'ai regarde les specifications filtraient a 20KHz pour une fe de 44.1KHz.
Pour les fe 88.2, 96 et plus, ils filtraient a fe/2.
Je serais etonne que ce phenomene se produise sur un convertisseur delta sigma.
scare
Citation :
Je serais etonne que ce phenomene se produise sur un convertisseur delta sigma.
Et moi aussi c'est ce qui m'étonne dans cette histoire. C'est pour ca que j'ai demandé à Danguit quelles puces sont dans ses convertos.
Pour moi le delta sigma s'affranchi de tout ça et c'est les converto Old school qui sont concernés.
Danguit : démonte ton converto ![]() et donne nous la ref de la puce !
et donne nous la ref de la puce !
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 11:51:03 ]
Anonyme
Dites, je voudrais pas faire mon rabat joie, mais le thread portait sur des tests réalisés en aveugle, et là vous partez quand même dans des explications ultra pointues. ![]()
scare
Citation :
Pour les fe 88.2, 96 et plus, ils filtraient a fe/2.
Si on jette un coup d'oeil au delta sigma AD1871 de chez analog dont le datasheet est bien détaillé :
- Apparemment pas de schéma de filtrage analogique en entrée proposé (il est possible d'en ajouter un généralement du premier ordre généralement)
Concernant le filtre passe bas de décimation en sortie, malheureusement il coupe toujours à partir Fe/2

![]()
Le voici :
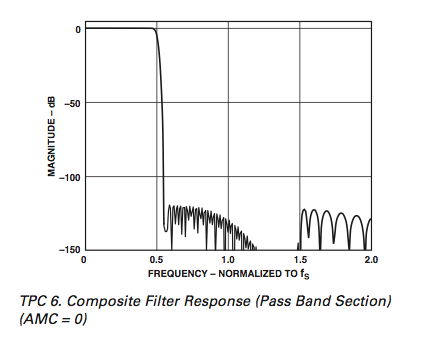
Les specs du filtre à 48 et 96 (pour 88,2 et 44,1 la doc indique d'utiliser la composite filter response) :
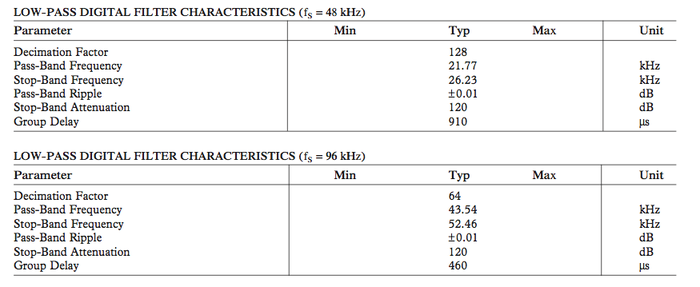
Ca sent pas bon DU TOUT !!!! pour 44,1 et 48.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 12:49:51 ]
jeriqo
Je parlais pour la marque AKM et pas Analog Devices mais c'est vrai qu'ils sont aussi utilises dans certaines machines haut de gamme, mais plutot en sortie.
scare
le meilleur de chez Texas instrument pcm4222 :
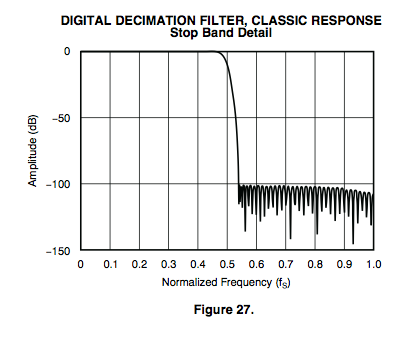
Aie aie aie
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 13:07:41 ]
scare
AKM 5394 :
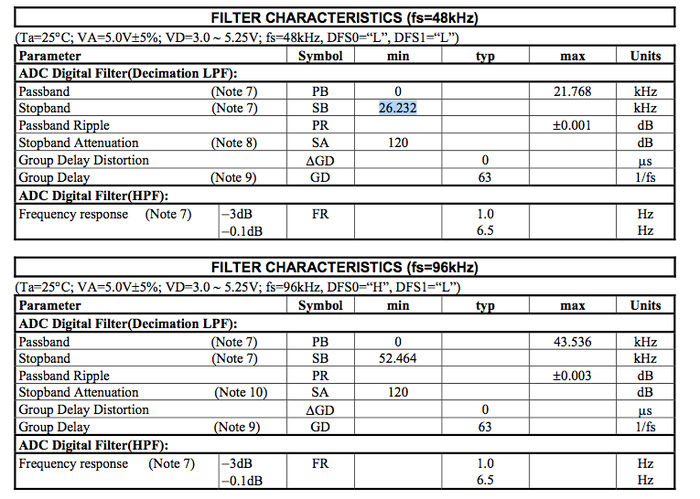
Pas mieux 
Ca sent les nems cramés
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 24/11/2010 à 13:13:47 ]
Danguit
Dr Pouet
Dites, je voudrais pas faire mon rabat joie, mais le thread portait sur des tests réalisés en aveugle
Oué, c'est pas faux.
Certes ça peut répondre à la question "a-t-on une chance de l'entendre ?" ; d'un autre côté on pourrait faire un autre thread plus spécifique...
scare
On peut donc en déduire que sur les delta sigma, tout ce qui sera entre Fe/2 et la "stop bande" sera replié.
C'est pour cela qu'à Fe = 44,1 Danguit voit sa raie de 22,6 repliée a 21,5.
A 96 kHz (ou 88,2), Fe/2 est tellement grand que le repliement est loin loin d'atteindre le spectre audio.
Exemple avec les specs du AKM :
à 48 kHz :
Fe/2 = 24 kHz et la stop bande indique -120 dB à 26,23 kHz => on peut donc s'attendre à un repliement jusqu'à 21,77 kHz (c'est short ...)
à 96 kHz :
Fe/2 = 48 kHz et la stop bande indique -120 dB à 52,464 kHz => on peut donc s'attendre à un repliement jusqu'à 43,536 kHz (on est large )
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Danguit
jeriqo
Citation de : scare
On peut donc en déduire que sur les delta sigma, tout ce qui sera entre Fe/2 et la "stop bande" sera replié.
C'est pour cela qu'à Fe = 44,1 Danguit voit sa raie de 22,6 repliée a 21,5.
Pourtant ce repliement serait du a l'aliasing genere lors de l'echantilllonage, qui est effectue a des frequences tres superieures sur un CAN delta sigma.
A mois qu'il ne vienne d'ailleurs.. ?
Danguit
Pourtant ce repliement serait du a l'aliasing genere lors de l'echantilllonage,
Je ne sais pas si c'est clair pour tout le monde, donc je re-précise : il y a deux phénomènes différents,
1. le fait qu'en sortie analogique, un signal proche de Fe/2 est distordu par l'ajout de son image (à 44.1k, le signal initial à 21.5k contient également du 22.6k). Cf. relevé précédent.
2. le fait qu'en entrée, les signaux supérieurs à Fe/2 sont repliés avec un niveau fonction du filtre anti-repliement (le 22.6k précédent se re-transforme en 21.5k).
scare
Citation :
Pourtant ce repliement serait du a l'aliasing genere lors de l'echantilllonage, qui est effectue a des frequences tres superieures sur un CAN delta sigma.
A mois qu'il ne vienne d'ailleurs.. ?
Il vient du filtre de décimation du CAN qui coupe juste après Fe/2 .... ce con ! que ce soit Analog, Texas ou AKM
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Anonyme
Hors sujet :
Citation :
Certes ça peut répondre à la question "a-t-on une chance de l'entendre ?"
Je me permets juste de revenir là dessus.
Si pour constater qu'un son est différent d'un autre on est obligé de faire des équations tirées de la physique quantique, c'est probablement que ces différences n'existent pas.
(bon, je force le trait, hein.)
Notez bien que je critique absolument pas cette démarche, il est effectivement intéressant de savoir comment et pourquoi les choses fonctionnent.
Anonyme
hmmm ... sans doute , mais ces types ont des oreilles bioniques .
Quoique , le dernier NIN on peut l'avoir en lossless FLAC et aussi en CD-quality , et là , y'a une différence audible . Un son plus "deep" et plus défini sur le FLAC que sur le Wav en 44100 ...
et l'album pèse dans les 2/3GO comme ça , mais c'est le son brut qui sort du studio de Trent Reznor ...
Anonyme
ouai, enfin si on commence à dire qu'il y a une différence audible entre le FLAC et le wav, on est pas sortie de l'auberge, parce qu'on peu aussi se lancer dans le wav contre l'aiff, ou l'usb contre le firewire! ![]()
jeriqo
C'est un flac 24/96 je crois alors que le wav est 16/44.1.
Peu improte wav ou flac en fait.
Dr Pouet
Message de modération :
Donc pour continuer les débats sur le repliement, les technologies de conversion et autres, faisons-le ici, et cessons le hors-sujet dans ce thread.
Merci de votre compréhension
scare
Hors sujet :
Dr Pouet, t'as pas moyen de copier tous nos posts techniques dans le nouveau sujet ? c'est chaud de redémarrer à blanc, on va plus rien capter
.
...Ou sinon tu copies tout le sujet et t'enlèves tous les posts "non HS"
ca sera plus rapide. Merci
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 25/11/2010 à 00:50:09 ]
Danguit
1. OK et d'accord avec scare.
2. Petite question : comment fait-on pour définir la limite du HS ?
Si l'on prend les items # 10 et # 41, il y est clairement indiqué (avec petit test à l'appui) qu'il peut y avoir des différences audibles par tous en fonction des fréquences d'échantillonnage. L'exemple était entre 44.1k et 96k car c'est plus parlant mais on pourrait le faire entre 44.1k et 48k avec des conclusions similaires.
Il me semble donc que cela répond à peu près à la question initiale.
Comme ces différences ne sont pas liées directement à la valeur de la fréquence d'échantillonnage mais sont dues à des imperfections des matériels, je ne vois pas trop comment présenter les choses sans entrer dans des détails techniques.
scare
Hors sujet :
et tous nos posts découlent de ces deux posts.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 25/11/2010 à 08:15:19 ]
mat from rieux
juste pour revenir au début des questions que posent ce thème, la fréquence d'échantillonnage à 44,kHz comme celle à 48 kHz découlent toutes deux de standard vidéos, ceci pour prendre en compte la possible compatibilité des enregistreurs de type vidéo lorsqu'ils sont utilisés comme moyen de stockage de l'information audio.
En effet, en NTSC la vidéo est en 59,94 Hz avec 525 lignes horizontales et 35 lignes blanches, soit 490 lignes actives par tranche, soit 245 lignes par champ. Si on stocke3 échantillons par ligne, alors la fréquence d'échantillonage devient:
59,94x245x3=44,09559 kHz
En PAL/SECAM la vidéo est en 50 Hz avec 625 lignes dont 37 blanches, soit 588 actives par tranche, soit 294 par champ:
50x294x3=44,1kHz
Bien que le CD n'ait pas de circuit vidéo, l'équipement utilisé pour faire les masters est basé sur la vidéo et fixe la fréquence d'échantillonnage à 44,1 kHz
pour le 48000 ce sont les mêmes considérations sauf que les standards pris en compte sont ceux de la vidéo numérique professionnelle et non plus les standards de la vidéos analogique du 44,1kHz
je pense qu'il n'y a pas de différences audibles entre les deux taux d'échantillonnages et si on augmente de beaucoup ce taux non plus toutefois un signal échantillonné en 96000 ou 192000 doit mieux supporter certains effets et en particulier le pitch (quand on le descend)ou le time stretch ...
j'espère que cette démonstration vous sera utile
bien a vous les AFposters
- < Liste des sujets
- Charte

