Audiofanzine a 25 ans !
Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
FR
EN
Notifications
  • Refonte graphique octobre 2025
    Refonte graphique octobre 2025
    Une refonte graphique vient d'être mise en ligne. Nous espérons qu'elle vous plaira. Merci de nous signaler tout bug ou perte de fonctionnalité ici →
  • Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Pour célébrer notre quart de siècle, UVI se joint à nous et vous offre le Digital Synsations Vol.1. Pour en profiter c'est par ici 👉
  • Nouveauté : Bookmark article, news ou tuto
    Nouveauté : Bookmark article, news ou tuto
    Bookmarkez un article, une news ou un tuto et retrouvez-le dans votre section "Mes signets" du menu membre.
  • 6 nouveaux annuaires
    6 nouveaux annuaires
    Luthiers, Réparateurs, Cours de musique, Studios d’enregistrement, de mastering et de répétition... Suggérez l’ajout d’une entreprise, inscrivez la vôtre ou déposez un avis.
  • Alertes disponibilité et baisse de prix
    Alertes disponibilité et baisse de prix
    Ces nouvelles fonctionnalités vous permettent d'être informé·e dès qu'un produit est disponible ou que son prix a baissé.
  • Tentatives d'arnaque dans les petites annonces
    Nous faisons face depuis quelques mois à une recrudescence de tentatives d'arnaques dans les petites annonces. Suivez nos recommandations >
Bidouille & Développement Informatique
News
Articles
Médias
Forums
Tutoriels

Le pub des programmeurs

  • 1 927 réponses
  • 117 participants
  • 131 707 vues
  • 130 followers
Sujet de la discussion Le pub des programmeurs
Salut :coucou: y a des programeurs sur AF si oui vous bossez sous quoi ?
Afficher le sujet de la discussion
976

Citation :
Tu regardes les annonces, dans 80-90% des cas c'est JAVA/J2EE ou C#, et le taff est dans le domaine des systèmes d'informations.



Franchement, c'est faux, ca depend des domaines. Il y a des pans entiers qui n'utilisent pas du tout ces langages. Je reconnais volontiers que ma vue soit biaisee "anglo saxonne", mais quand meme. En particulier, perl est encore vachement demande (plus que python + ruby reunis, je pense, et de loin), sans compter le C evidemment, ou javascript.

Le java et le C# sont tres demandes, c'est indiscutable, mais le sont dans certaines domaines plus que d'autres. Ca depend des domaines.

Citation :

Mais bon, moi, ce que j'en pense de l'auto-formation, c'est que c'est pas reconnu par les employeurs. A mon avis, il vaudrait mieux utiliser les congés de formation ou droit individuel à la formation.



Ou peut quitter le marche francais, aussi, mais c'est un choix qui n'est pas donne a tout le monde :)
977

Citation : ce que j'en pense de l'auto-formation, c'est que c'est pas reconnu par les employeurs.


Mouais, je sais pas: ya un tas de gens qui aprennent des langages tout seuls et qui s'en sortent. Mon ancien bassiste a une formation de microbiologie (un truc balèze en bac+5 au moins), il s'est formé seul au web (PHP et autres SQL ou flash) et aujourd'hui il est webmaster d'une grosse boite de softs 3D + il a monté sa boite à côté, question boulot il débande pas...

Mon studio

Allez viens mixer avec tes copains

978

Citation :
En fait je voulais juste dire qu'apprendre l'objet est utile, voire nécessaire. Après c'est bien de pouvoir le faire avec un langage qui en plus peut constituer une compétence recherchée.



Oui, bien sur, je me suis peut etre mal exprime: je pense que pour apprendre l'objet, il vaut mieux commencer par python/etc... et APRES, bien sur, apprendre java/C#, qui sont clairement les deux langages objets les plus demandes. Je sais que perso, je suis nettement meilleur en C++ et meme en C depuis que j'ai appris un langage plus expressif, par exemple (java/C# m'interessant absolument pas pour ce que je veux faire).

@ Bara, je pense que ce qu'il voulait dire, c'est qu'en France, on est plus regardant sur l'experience/les diplomes qu'ailleurs, ce qui est assez vrai selon mon experience et les retours que j'ai aussi.
979

Citation : Mouais, je sais pas: ya un tas de gens qui aprennent des langages tout seuls et qui s'en sortent. Mon ancien bassiste a une formation de microbiologie (un truc balèze en bac+5 au moins), il s'est formé seul au web (PHP et autres SQL ou flash) et aujourd'hui il est webmaster d'une grosse boite de softs 3D + il a monté sa boite à côté, question boulot il débande pas...



En fait, ce que je voulais dire, c'est que tu as tout intérêt à demander un congé de formation, ou utiliser ton droit à la formation pour effectuer une formation à ces langages dans une boite de formation qualifiée plutôt que d'apprendre par toi-même. Tu n'apprendras p-e pas autant de chose, mais du point de vue de tes futurs employeurs, ta qualification sera reconnue. Je ne doute pas qu'on puisse y arriver sans, mais c'est quand même plus difficile d'ouvrir des portes quand on s'est formé tout seul ;)
980

Citation : Mais bon, moi, ce que j'en pense de l'auto-formation, c'est que c'est pas reconnu par les employeurs. A mon avis, il vaudrait mieux utiliser les congés de formation ou droit individuel à la formation.


L'idéal, si possible : faire de l'auto-formation, parce-que ça fait de la pratique, et que c'est le seul moyen d'être vraiment compétent ; et suivre une formation pour avoir le bout de papier qui dit "compétent en XX"...

Citation : Meme le bouquin des design pattern, je ne le trouve pas tres bon en soi. C'est une reference, pas de doute, mais pour apprendre et comprendre les principes, je suis pas si convaincu.


Exact. Si on se démerde déjà en objet, ça ouvre des perspectives, ça ajoute des idées que l'on a pas déjà eues, ou ça permet de mieux le manipuler... Par contre c'est loin d'être le top pour découvrir l'objet. Mais je ne sais pas s'il y a un bon bouquin là-dessus. A mon avis la bonne piste est de trouver un bon tutoriel sur des widgets graphiques. Ca fournira une formation par la mise en pratique (en plus d'acquérir une compétence sur lesdits widgets).


Citation : Ben ce sont des exemples usuels que tout le monde est capable de comprendre. Ca peut être sur une voiture qui est un véhicule, un choux qui est un légume, ...
Le tout étant de savoir dans quel contexte on se trouve.
On avait eu un exercice en cours : faire une hiérarchie objet des objets de cuisine. On bosse 5 minutes puis le prof nous dit qu'il nous manquait une information essentielle que personne n'a demandée : selon quels critères on fait la hiérarchie.


Citation : C'est beaucoup plus puissant de penser en terme de protocole, d'API, de message passing


Ben il me semble que vous êtes d'accord : l'héritage se définit par des API communes. "Les critères" = "les services dont on va avoir besoin" = l'API.

Si on considère les éléments d'un dessin vectoriel, ils vont tous avoir une méthode "dessiner()". On va les ranger dans une liste, et les dessiner en partant du fond vers l'avant. Le point n'aura pas de méthode "redimensionner(..)" alors que la plupart des autres objets l'auront. Les surfaces auront "définir_couleur_remplissage(..)" alors que les traits et le texte non. etc...

Dès que tu as déjà un peu programmé, tout ça est très concret. Alors que le fait qu'un éléphant soit un mammifère, en C++ on voit pas très bien ce que ça donne !

Citation : > Tu regardes les annonces, dans 80-90% des cas c'est JAVA/J2EE ou C#, et le taff est dans le domaine des systèmes d'informations.

Franchement, c'est faux, ca depend des domaines. Il y a des pans entiers qui n'utilisent pas du tout ces langages.


Probablement 80% des offres d'emploi sont sur des SI. Mais si tu fais du calcul scientifique (2% du marché ?) c'est C / Fortran. Si tu fais de l'embarqué (encore 2% du marche ?) c'est C, Ada, SDL... Si tu fais du bancaire / gestion, va y avoir du Cobol, si c'est du web : php, SQL, javascript, flash... etc
Là aussi vous avez probablement pas mal raison tous les deux !

C'est bien l'homme qui cause le dérèglement climatique - AudioFanzine sans PUBlicité

981

Citation :
Probablement 80% des offres d'emploi sont sur des SI.



T'as des chiffres concrets ? En fait, je me demande vraiment quels sont les chiffres, en admettant que ce soit possible d'en avoir. En tout cas, aux US, C#+java, ca fait pas 80 % des offres d'emploi, aucun chiffre que j'ai pu voir ne donne cet ordre de grandeur.

Tout chiffre est discutable, c'est clair, mais par exemple, je me souviens de ca:

http://radar.oreilly.com/archives/2006/08/programming_language_trends.html



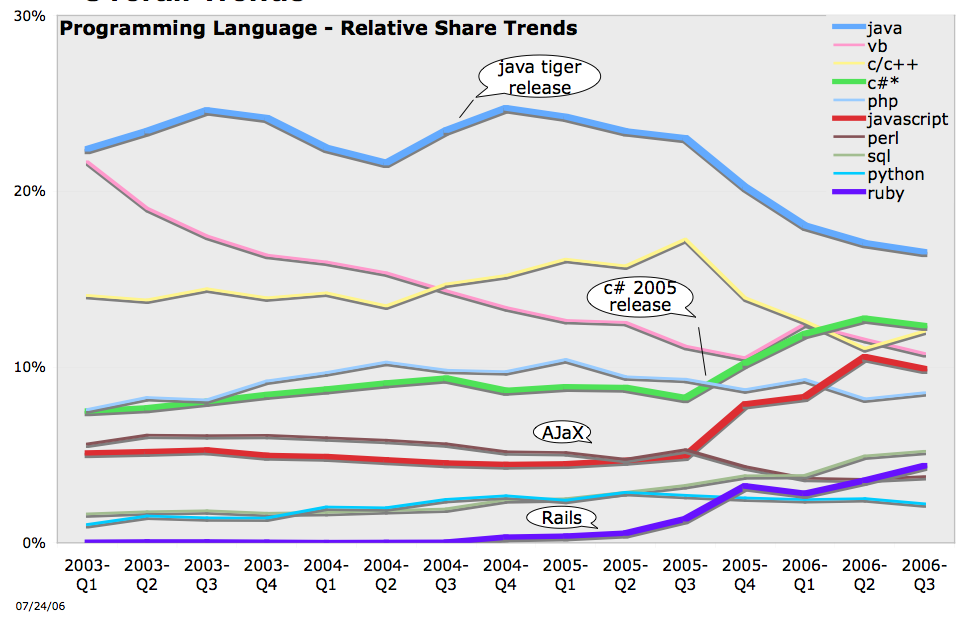
Ou tu vois que le javascript est eu meme niveau que le C#, que le java baisse (mais c'est surement a cause de C# et de la montee des serveurs windows au detriment des unix proprietaires, enfin c'est l'hypothese la plus evidente qui vient), que le VB aussi baisse pas mal (par exemple, etant pas mal implique dans les calculs numeriques et python, je sais que python et les autres langages dynamiques montent pas mal pour la finance, qui est un domaine qui est trs utilisateur de VB. Tu ajoutes le fait que python est officiellement supporte par la CLI et que VB .net est incompatible avec VB 6, et tu as surement l'essentiel de cette progression, je pense).

Donc que le java et le C# soient des langages tres courants, voire les plus courant, c'est indeniable. Que ce soit 80 % du marche, je suis beaucoup plus circonspect.
982
Un peu de documentation sur la programmation bas niveau.

C'est bien l'homme qui cause le dérèglement climatique - AudioFanzine sans PUBlicité

983
Argl !! J'ai loupé le début de la discussion !!

bara > tu veux changer de boulot ?

Effectivement, Java et .Net dominent le marché, mais pour bara, je pense qu'il y a bien plus à valoriser dans l'informatique scientifique. Dans ce domaine, on fait du C/C++/Fortran, et par-dessus du Matlab ou du Python pour le prototypage (de plus en plus c'est le cas, par exemple chez Shell).
Tu es bon en bas niveau, ce qu'il te manque, c'est une couche par-dessus pour le prototypage, les maquettes, car ton passé de chef de projet t'ouvrira des portes. Donc je ne peux que te conseiller de te mettre à Python.

Si tu fais de la formation auto-didacte, il ya un moyen simple de la valoriser : un blog. Régulièrement, tu montres dedans ce que tu sais faire (ex : http://matt.eifelle.com ou cournape.wordpress.com) et ça te fera une carte de visite supplémentaire que les techniciens pourront regarder pour voir si oui ou non tu maîtrises ton sujet. C'est un point qui est apprécié (dixit une journaliste spécialisée dans le recrutement moderne).

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

984
Gabou > ce sont les ventes de livres, ça ne reflètent malheureusement pas la réalité des faits. D'autres chiffres de vente de livres, montrent une autre tendance, ça dépend :
- si la bibliothèque personnelle/professionnelle est bien fournie (comme pour le C ou le C++)
- si la librairie est touffue en terme d'ouvrages
- ...

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

985
Une autre façon de montrer que tu es compétent est de t'investir dans le logiciel libre. De cette manière, tu as des morceaux de ta création en circulation un peu partout et n'importe qui peut attester que tu as des compétances dans tel ou tel domaine.
Perso le fait d'avoir fait un projet opensource assez utilisé m'a ouvert des portes et ce n'est pas fini :)
986

Citation :
Gabou > ce sont les ventes de livres, ça ne reflètent malheureusement pas la réalité des faits. D'autres chiffres de vente de livres, montrent une autre tendance, ça dépend :



Oui, je suis bien conscient que ce n'est qu'un point, et que c'est tres discutable. Mais est-ce que c'est moins valable que de dire "80-90% des offres sont java et .net ?" C'est tres facile quand on est dans un domaine de generaliser a un autre, ce qui fait qu'avoir des chiffres "exterieurs" peut donner un autre point de vue (si je me fiais a mon propre environnement, java et .net feraient genre 10 %, fortran + C + C++ 50 %, et python/ocaml/lisp/haskell le reste. Mais bon, c'est clairement pas la tendence generale tout domaine confondu).

Citation :
Une autre façon de montrer que tu es compétent est de t'investir dans le logiciel libre. De cette manière, tu as des morceaux de ta création en circulation un peu partout et n'importe qui peut attester que tu as des compétances dans tel ou tel domaine.



C'est clair. Perso, j'ai eu des offres spontanees assez interessantes aussi bien sur le plan technique que financier par ce biais.

Hors sujet : > miles1981: tu peux de nouveau compiler numpy avec numscons et ma plateforme/compilo preferes... J'en ai chie, mais ca marche enfin, du moment que t'as pas besoin d'incorporer du fortran. Entre autre, avec mon installer, tu peux avoir ATLAS optimise + VS 2003, yeah !

987

Hors sujet : Faudra que je réesaie sous Widnows, sous Linux, je ne passe pas par setupscons, faudra que j'essaie pour voir ;)
J'ai peu de temps pour ça actuellement (rédaction de thèse) mais dès que j'en ai, j'essaie, promis ;)

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

988
Pour ceux que ça intéressait : http://www.pdp2008.org/nvidia.html

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

989
Oh my God!!
Vous avez vu ça??? :oo:
http://www.sonicstate.com/video/index.cfm?vid=1
990
Tu parles de quelle vidéo exactement ? Il y en a une pétée ... La pédale de Line6, les VST sans ordis, ... ??

cptn.io

991
Vu l'excitation sur les forums anglo-saxons et le fait que nous sommes dans un fil dédié à la programmation, Guitoo faisait sûrement allusion au Direct Note Access de Melodyne.

http://www.sonicstate.com/news/shownews.cfm?newsid=6281
https://www.celemony.com/dna_standalone/eu/dna.html

:mrg:

« What is full of redundancy or formula is predictably boring. What is free of all structure or discipline is randomly boring. In between lies art. » (Wendy Carlos)

992
Oups je pensais que ma page pointais sur la bonne video.
J'en ai parlé brièvement avec un de mes encadrant de thèse tout a l'heure. Les chercheur qui font du MIR (Music information retrieval) S'interroge pas mal sur la méthode employée et il semblerait que DNA utilise une méthode qui lui est propre.
993
Une petite ICA couplée avec une reconnaissance monophonique ?

http://blog.audio-tk.com/

Audio Toolkit: http://www.audio-tk.com/

994
Globalement c'est surement ça. A la fin de la vidéo il avoue que ça ne marche pas quand il ya des modulation ou des glides.
Mais a un moment on voit qu'il arrive a séparer 2 notes a l'octave simultanée. Donc c'est pas une ACI classique.

Sinon je trouve ça sympa que ce soit le chercheur lui même qui vient parler de sa technologie et que les gens soit intéressés. J'adore le style bien geek du chercheur des années 70.
995
Mmhh juste en passant, dsl de détourner le sujet, est-ce que qqun ici maitrise les fpga, et les adc ? mici ^^

cptn.io

996
Maitriser serait un bien grand mot pour moi, mais disons que je planche actuellement sur ce sujet (FPGA + codec audio).

Et si je peut t'aider et si tu pouvais m'aider...
997
Salut tout le monde

une question qui arrive comme un cheveu sur la soupe :mrg:

Dans quel format je dois exporter mon animation flash si c'est pour l'importer par la suite dans une page HTML ?
998
Ba tu la prends en swf, et tu mets un lecteur de swf dans ta page...

cptn.io

999

Citation : tu mets un lecteur de swf dans ta page



aie...je ne sais pas faire ça...je vais essayer de trouver un tuto sur ce sujet
1000
Tu te sers de quelle interface pour faire ton anim flash ?
Flash ou Flex builder ?
Les deux peuvent te créer une template html( un bout de code que tu copies colle dans ta page html).
Mais demandes plutot sur des forums spécialisé ou crée un thread.

http://soundcloud.com/bat-manson