Dans les précédents articles, nous avons exploré le cœur des sons et y avons découvert les ondes et ce qui les définit.
À présent, il est temps de nous pencher sur les principales formes que celles-ci peuvent adopter en tant qu’ingrédients de base de toute « cuisine » sonore. J’indiquerai autant que possible les termes anglais correspondants entre parenthèses, car ne nous leurrons pas, la quasi-totalité des appareils de synthèse sont labellisés dans la langue de Shakespeare.
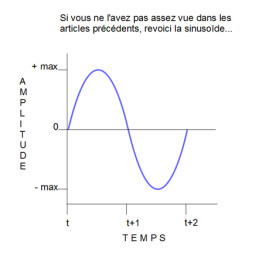
Sinusoïde (anglais : sinus)
Comme nous le verrons, la sinusoïde est à l’origine de toutes les formes d’ondes que nous allons lister dans ce chapitre, à l’exception des grains dont nous parlerons en fin d’article.
Nous avons déjà amplement fait connaissance avec elle au cours des précédents articles. Nous avons appris, notamment, que cette forme d’onde est la plus simple qui soit — un son fondamental, accompagné d’aucun autre son, ni harmonique ni inharmonique – et également que sa fréquence définit la hauteur du son concerné.
De par sa « simplicité », le son produit par une sinusoïde est également le plus pauvre harmoniquement des sons produits par les formes d’ondes présentées ici.

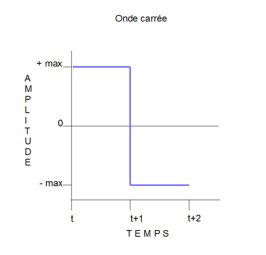
Onde carrée (anglais : square)
L’onde carrée diffère de l’onde sinusoïdale en ce qu’elle contient, en plus du son fondamental, des harmoniques impairs. C’est la somme de celles-ci s’ajoutant au son fondamental qui permet d’obtenir la forme carrée de cette onde. La puissance des harmoniques d’une onde carrée décroît selon la formule 1/f, où f est égal à la valeur de la fréquence concernée.
Comme nous le voyons, l’onde carrée passe la moitié du cycle à amplitude constante au-dessus du point d’équilibre et l’autre moitié du cycle au-dessous. On dit alors de l’onde qu’elle est symétrique et on parle d’onde carrée véritable. Si ce n’est plus le cas, c’est-à-dire si le temps passé au-dessus du point d’équilibre diffère de celui passé au-dessous, l’onde n’est plus symétrique, et l’on parle alors d’onde « rectangulaire ».
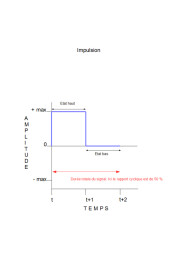
Impulsion (anglais : pulse wave)
L’onde impulsionnelle est un exemple d’onde asymétrique issue de l’onde carrée. Dans son cas, on dit que l’onde alterne entre un « état haut » et un « état bas ». Ce dernier peut correspondre à la valeur « 0 » d’amplitude, mais pas obligatoirement. La fraction de temps que l’onde passe en « état haut » par rapport au cycle complet s’appelle le « rapport cyclique » (« duty cycle » en anglais).
Nous étudierons d’ailleurs dans un prochain article ce qu’il advient lorsque l’on modifie le rapport cyclique en temps réel au travers de la MLI – Modulation de Largeur d’Impulsion, terme barbare sous lequel se cachent des possibilités de manipulation sonore tout à fait intéressantes !
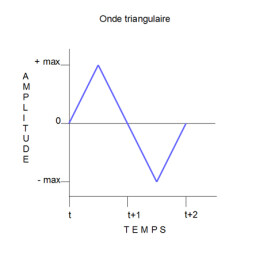
Onde triangulaire (anglais : triangle)
L’onde triangulaire est comparable à l’onde carrée en ce qu’elle contient également des harmoniques impairs en plus du son fondamental. Mais elle se différencie toutefois de l’onde carrée principalement en ce que la puissance desdites harmoniques décroît selon la formule 1/f² où f est égal à la valeur de la fréquence concernée.
Une onde triangulaire peut être plus ou moins symétrique.
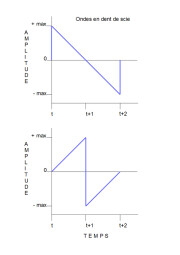
Onde en dents de scie (anglais : sawtooth)
C’est la forme la plus extrême d’onde triangulaire asymétrique. Elle peut avoir deux formes : une rampe montante progressive suivie d’une chute abrupte, ou bien une montée instantanée suivie d’une descente progressive.
Au niveau fréquentiel, l’onde en dents de scie est la plus riche en harmoniques. C’est bien simple : elle les contient tous ! Cette richesse la rend particulièrement intéressante pour la synthèse soustractive, comme nous le verrons dans un prochain article.
- Saw montante 00:01
- Saw descendante 00:01
Grains
Il s’agit de la source sonore de base de la synthèse granulaire sur laquelle – devinez quoi ? — nous reviendrons dans un prochain article. Nous touchons là à une forme complexe de source sonore qui dépasse la simple forme d’onde. Cette sorte d’élément – et le type de synthèse qui en résulte – n’existe que dans le domaine numérique, aucun appareil analogique ne pouvant les produire.
En effet, un grain regroupe non seulement une forme d’onde donnée, mais également un point de départ, une durée et une enveloppe (nous verrons de quoi il s’agit… dans un prochain article). Les grains contiennent également, stockés sous forme numérique et donc immédiatement accessibles et modifiables via l’outil informatique, des informations fréquentielles telles que la période de la forme d’onde concernée ou bien encore son spectre.
La forme d’onde contenue dans le grain peut être « synthétique » ou « échantillonnée ». Dans le premier cas, il s’agit de formes d’ondes classiques, « synthétisées » traditionnellement selon une somme de sinusoïdes de base. Dans le second cas, il s’agit de sons numériquement enregistrés – échantillonnés — au préalable, et classés de manière ordonnée dans ce que nous appelons une table d’ondes – un tableau dont chaque case, contenant un son, serait identifiée par des coordonnées de type X, Y pour en autoriser l’accès et la lecture. La synthèse par tables d’ondes sera, elle aussi, étudiée de manière plus approfondie dans un prochain article. À noter que synthèse granulaire et par table d’ondes ne se recoupent pas nécessairement.
L’exemple sonore suivant montre un son avant et après « granularisation » extrême.