Comme nous l'avons vu dans l'article précédent, si la forme d’onde est répétitive, on dira qu’elle est périodique.
Répétition
D’un point de vue théorique et à titre d’exemple, les notes de musique sont toutes basées sur une forme d’onde périodique. À l’inverse, le bruit ne repose pas sur une forme d’onde périodique : on ne peut pas établir de schéma de répétition pour une forme d’onde représentant du bruit. Entre les sons basés sur les formes d’onde périodiques et les bruits se situent tous les autres sons.
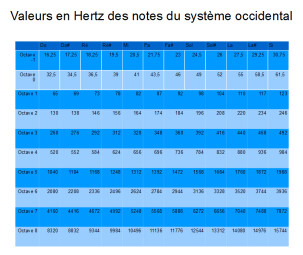
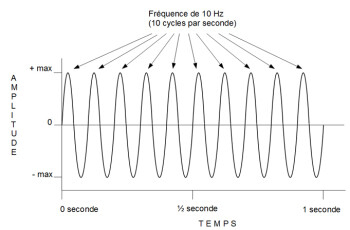
Toujours d’après le précédent article, les ondes périodiques sont composées de cycles. Le nombre de cycles que l’onde effectue en une seconde détermine sa vitesse d’oscillation, mais pas sa vitesse de propagation, qui restera la même tant que le milieu – « élastique », rappelez-vous le premier article ! – ne change pas. La vitesse d’oscillation d’une onde est exprimée en Hertz (Hz), du nom de l’acousticien allemand Heinrich Hertz, et porte le nom de « fréquence ». Par exemple, la note La émise par un diapason ou un instrument de synthèse sonore est constituée théoriquement d’une seule sinusoïde simple d’une fréquence de 440 Hz.
D’une octave à l’autre, le nombre de Hz est multiplié par 2 pour une même valeur de note.
Le géant et le nain
Pour bien comprendre la différence entre la fréquence (vitesse d’oscillation) d’une onde et sa vitesse de propagation, considérons un géant et un nain qui parcourraient la même distance — disons 340 mètres au hasard — dans le même laps de temps – disons 1 seconde. Tous les deux feraient donc du 340m/s. Mais là où le géant n’aurait par exemple que vingt pas à faire pour franchir les 340 mètres en 1 seconde, le nain en aurait, allez, disons 20000 (ce serait plutôt un schtroumpf, et vraiment petit…).
Bien que la vitesse de déplacement ou « propagation » – 340m/sec – soit la même pour le géant et pour le micro-schtroumpf, leur nombre de pas diffère : 20 pas pour le géant et 20000 pour le micro-schtroumpf. Ramené au domaine audio, on pourrait donc dire que le géant est une onde à 20 Hz (20 « pas » ou cycles par seconde) et le schtroumpf une onde à 20000 Hz (20000 « pas » ou cycles par seconde).
Bon allez, je vous révèle un secret, je n’ai pas pris ces chiffres au hasard en fait… En effet, 340 m/s est la vitesse moyenne de déplacement du son dans l’air – variable selon la température ! – et 20 et 20000 Hz (20 kHz) sont les limites basse et haute des fréquences que notre ouïe peut théoriquement percevoir.
Ach, Monike…
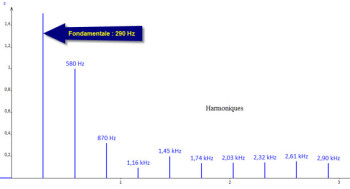
Nous avons vu qu’une note de musique est basée sur une fréquence donnée – 440 Hz pour reprendre l’exemple du La émis par un diapason. Toutefois, comme je l’ai déjà dit précédemment, une note pure ne se rencontre quasiment jamais dans la nature. Elle est la plupart du temps jouée par des instruments, que notre ouïe est tout à fait capable d’identifier. Or si notre ouïe est en mesure de différencier une voix humaine, un steel-drum ou un hautbois, c’est donc que l’onde sonore émise par chacune de ces sources, même si elle véhicule toujours l’information « La 440 Hz » dans notre exemple, contient également d’autres informations sonores qui rendent possible son identification.
On parle alors de son fondamental pour la fréquence de 440Hz de notre exemple, et de sons « harmoniques » et partiels pour toutes les informations sonores supplémentaires qui vont caractériser le son. Le son fondamental est celui qui définit la hauteur générale du son. Les sons harmoniques qui l’accompagnent sont les multiples entiers de la valeur du son fondamental. À noter que les harmoniques pairs sonnent en général mieux à notre oreille que les harmoniques impairs.
Les partiels sont les éléments du son global qui ne sont pas des harmoniques du son fondamental. On dit donc qu’ils sont « inharmoniques ». On peut observer que plus la valeur en Hz des harmoniques et partiels s’éloigne de celle du son fondamental, plus le volume sonore des compagnons du son fondamental décroît globalement. L’ensemble de tous les éléments qui constituent un son – son fondamental, sons harmoniques et inharmoniques – s’appelle le spectre sonore.
Comme dit plus haut, ce sont ces sons accompagnants qui définissent la nature du son produit. Comprendre leur rôle est indispensable principalement dans le cadre de la synthèse additive et de celle par modélisation, cette dernière s’attachant particulièrement à recréer artificiellement des sonorités réelles. Mais nous nous intéresserons aux différents types de synthèse plus tard. Le prochain article, quant à lui, sera dédié aux formes d’ondes de base que nous pouvons trouver sur un synthétiseur !