Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
Notifications
< Retour vers Synthèse Sonore
Agrandir
Synthèse Sonore
Techniques du Son
Synthèse Sonore
Actu 32 32
Articles 37 37
Médias 306 306
Tutoriels Tutos 6 6
Forums 475 475

TIPE synthese sonore: analyse/resynthese additive par temps fréquence

  • 181 réponses
  • 10 participants
  • 20 500 vues
  • 12 followers
Sujet de la discussion TIPE synthese sonore: analyse/resynthese additive par temps fréquence
Bonjour à tous,
Voilà, je dois présenter un TIPE sur la synthèse sonore analogique en vue de passer des concours des grandes écoles.
Je voudrais savoir si certains pouvaient m'indiquer des livres (ou site si ça existe) qui approfondissent ce thème (au moins des auteurs).
Ma difficulté est de comprendre le principe de la synthese FM (pas du pt de vue mathematique mais du pt de vue réalisation). En fait j'aimerais savoir si on pouvait me donner de quoi elaborer une simulation de montage qui utiliserait le principe de la FM.
De même je cherche une idée ou quelques conseils pour realiser un montage qui simule une synthèse AM (multiplieur etc...) car je connais bien le principe mais je vois pas quel algorithme appliquer pr avoir des sons semblables à ceux d'instruments de musique par exemple.
Le but final est de faire une experience au labo de physique et de faire une analyse spectrale du signal emis (par exemple le son d'une guitare) et de le comparer au signal qu'on a voulu imiter.
Aussi, je voudrais savoir si qqun pouvait m'indiquer un site où l'on peut trouver l'analyse spectrale de différents instruments de musique (peu importe lesquels)
Merci à vous.
Afficher le sujet de la discussion
101
Ben c'est un graphique avec en abcisse la fréquences , en ordonnée l'amplitude , et avec pour troisième axe le temps, moi j'ai ce graphique et j'aimerais faire le chemin inverse , en obtenir un son. :D:
102
Salut,
Si tu connais les partiels et leur evolution au cours du tps, il est clair que tu peux créer le son : Moi j'ai fait comme ceci pour mon tipe :
- créer une liste contenant les liste relatives a chaque partiel ([frequence,temps,amplitude] où temps est l'instant correspondant a une fenetre) puis il reste a interpoler ceci par regression lineaire (enfin passer au log d'abord) ce qui donne des enveloppes exponentielles (d'ailleurs ca n'a rien donné de concluant sur mon exemple car mes points étaient "mal placés" a cause je pense du fenetrage rectangulaire qui fait perdre pas mal d'information).
Sur ces bonnes paroles, je pars à paris passer mon tipe dans quelques heures, je vs direz comment ça s'est passé.
103
De stress, finger in the noise

crois me, avec le taf que t'as fait, si les gars te demeontent c'est uniquement pour voir comment tu reagis quand on te destabilise.

Sois confiant, sur de toi (y a de quoi), et montre leur comment le sujet est difficile mais passionnant. Bon courage :coucou:

Site personnel: https://www.enib.fr/~choqueuse/

104
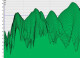
Je vais vous montrer mon graphique vous me dites ce que vous en pensez....voila:

Ca c'est l'enveloppe , normalement il n'y a que les partiels , n=1 ..15 , qui corespondent a la fondamentales et aux harmoniques
105
Y a beaucoup de variation dans l'amplitude, faut que t'arrive a obtenir une enveloppe qui ressemble plus a une eponentielle decroissante :boire:

Site personnel: https://www.enib.fr/~choqueuse/

106
T'aurais pas un graphique pour me faire une idée :lol:
107
Le graph represente une enveloppe spectrale, si je comprends bien ? Il est un peu bizarre, ce schema, tu l'as obtenu comment (quelle longeur de fenetre, quelle fenetre, taille FFT, overlap...) ? Si tu n'as pas tous les parametres de la representation temps frequence, il y a peu de change d'avoir un resultat satisfaisant pour la resynthese.
108
Euh bon alors en fait j'ai créer une fonction y qui représente la vibration de la corde de guitare, il se trouve que c'est une somme infini de partiel yn ;
y(x,t) = somme ( yn(t)* sin ( n pi x/ L)
j'ai pris les Yn qui correspondent aux partiel et j'en ai fait un graphique. Peut etre qu'il faut que je passe en log non?

J'obtient à l'instant initiale:
109
:((( Help
110
Yo

y(t)=sum_{n=1}^{N} A_{n}(t)sin(2*pi*f_{n}t)

la c'est bien A_{n}(t) que tu nous montres (pour un certain n) ?

C'est quoi ton probleme exactement

Ps: j'ai mis un programme d'analyse roots en matlab sur mon site dans la rubrique synthese)

Site personnel: https://www.enib.fr/~choqueuse/