Audiofanzine a 25 ans !
Se connecter
Se connecter
Mot de passe oublié ?
ou
Créer un compte
ou
Se connecter avec Facebook
FR
EN
Notifications
  • Refonte graphique octobre 2025
    Refonte graphique octobre 2025
    Une refonte graphique vient d'être mise en ligne. Nous espérons qu'elle vous plaira. Merci de nous signaler tout bug ou perte de fonctionnalité ici →
  • Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Un cadeau d'UVI pour les 25 ans d'Audiofanzine
    Pour célébrer notre quart de siècle, UVI se joint à nous et vous offre le Digital Synsations Vol.1. Pour en profiter c'est par ici 👉
  • Nouveauté : Bookmark article, news ou tuto
    Nouveauté : Bookmark article, news ou tuto
    Bookmarkez un article, une news ou un tuto et retrouvez-le dans votre section "Mes signets" du menu membre.
  • 6 nouveaux annuaires
    6 nouveaux annuaires
    Luthiers, Réparateurs, Cours de musique, Studios d’enregistrement, de mastering et de répétition... Suggérez l’ajout d’une entreprise, inscrivez la vôtre ou déposez un avis.
  • Alertes disponibilité et baisse de prix
    Alertes disponibilité et baisse de prix
    Ces nouvelles fonctionnalités vous permettent d'être informé·e dès qu'un produit est disponible ou que son prix a baissé.
  • Tentatives d'arnaque dans les petites annonces
    Nous faisons face depuis quelques mois à une recrudescence de tentatives d'arnaques dans les petites annonces. Suivez nos recommandations >
Techniques du Son
News
Articles
Médias
Forums
Tutoriels Tutos

Théorème de Shannon.

  • 103 réponses
  • 12 participants
  • 4 809 vues
  • 20 followers
Sujet de la discussion Théorème de Shannon.
Bonjour,
Je viens vous poster une question de mathématiques.

Le théorème d’échantillonnage de Shannon, qui prévoit une fréquence égale au moins au double de la fréquence maximale du signal est il résolu pour des valeurs d'échantillons appartenant à R (ensemble des nombres Réels) ou pour un ensemble fini comme 3 bits, ou 24 Bits par exemple?

je parle d’échantillonner un signal évidemment continu (audio).

Merci par avance,
2
Le pourquoi du comment est expliqué là :
https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d%27%C3%A9chantillonnage

Le nombre de bits n'affecte que la résolution du convertisseur A/D utilisé: 8 bits = 2^8 niveaux possibles soit 256, 16 bits = 2^16 = 65536 etc... Tant qu'il est capable de suivre la fréquence d'échantillonnage, qui elle doit respecter les principes de MM. Shannon et Nyquist, peu importe. Par contre pour la qualité de la restitution sous forme analogique (via un convertisseur D/A) il vaut mieux "trop" que "pas assez", les signaux de faible amplitude risquant de n'être codés que sur 2 ou 3 bits, voire pas du tout.
Hope that it helps...;)

[ Dernière édition du message le 11/05/2018 à 21:11:40 ]

3
Ok, merci,
Car moi je croyais que ce Théorème était résolu dans R seulement, et qu'en fait ce signal échantillonné dans R, composé de n valeurs d'échantillons, après on le quantifiait au plus près, disons 16 ou 24 bit, mais que cela ne pouvait plus être considéré comme "Parfaitement Fidèle" au signal continu, mais avec un taux d'erreur qu'on essaye de garder au plus bas.

J'ai du me tromper alors,

Merci pour tout.
4
Je ne comprends pas trop. Si tu penses que ce théorème est valable pour des valeurs choisies dans R, il l'est donc également si ces valeurs sont choisies dans une partie de R. Les nombres codables en 16 bits, par exemple, sont dans R. Non ?
5
Oui mais le signal à coder est continu (signal physique audio)
6
La quantification en amplitude et l'échantillonnage temporel sont des choses essentiellement indépendantes.

Par exemple, le théorème de Shannon s'applique aussi pour les BBD (lignes à retard), qui sont échantillonnées temporellement mais qui restent analogiques en amplitude.

Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts

7
Par contre si tu veux me démontrer que l’échantillonnage à la fréquence de Nyquist de ta courbe approximative à 16 bits est parfaitement fidèle à ta courbe approximative à 16 bits du signal, pourquoi pas, ça reste des approximations.
8
Moi j'ai juste l'impression qu'un signal échantillonné en valeur fini ne peut jamais être parfaitement fidèle à un signal continu. Çà reste des approximations, plutôt très bonnes par ailleurs, mais des approximations, comme tout en numérisation.
9
Oui, la numérisation dégrade le signal.

Le signal est continu jusqu'au micro (vibration de l'air).
Il est converti par le micro en signal électrique, toujours continu, jusqu'à l'entrée de la carte son.

A l'entrée de la carte son, il est converti en signal numérique.
C'est à dire qu'il est codé, transformé en un ensemble discret de points.

Il n'est donc plus continu, si du moins on parle de la manière dont il est enregistré.
Mais lorsqu'il sera écouté, le haut parleur opérera la transformation inverse, et émettra de nouveau un signal physique continu.


Même si le micro et le haut parleur étaient parfaits (ce qui est loin d'être le cas), cette quantification numérique, c'est à dire ce saucissonnage du son, produisent une légère déformation du signal. Plus la quantification est précise, et plus cette déformation est réduite.

Shannon parle de la fréquence d'échantillonnage. Il dit qu'il ne faut pas espérer enregistrer un son de 2000 Hz avec un fréquence d'échantillonnage inférieure à 4000 Hz, ce sera mathématiquement impossible.

Attention de ne pas en déduire qu'une fréquence de 4000 Hz permet d'enregistrer correctement tout ce qui est en dessous de 2000 Hz. Un signal de 1900 Hz, par exemple, va être sensiblement dégradé par un échantillonnage à 4000 Hz.

[ Dernière édition du message le 11/05/2018 à 23:23:12 ]

10
OK trazom, je crois que je vois les choses à peu près comme toi.
11
Cool, alors bonne nuit.
12
je suis pas sur de comprendre la question... mais l'échantillonnage ne fait que "ponctionner" des valeurs à une fréquence donnée.
C'est la résolution ensuite qui détermine l'ensemble des valeurs possibles.
Plus la fréquence d'échantillonnage est élevée, plus le nombre de valeurs comprises dans l'échelle des possibles sera grand, mais pour autant le nombre de valeurs dans cette échelle ne dépend que de la résolution.
Plus la résolution sera importante en revanche, plus la finesse d'approximation sera précise. C'est la combinaison des deux (fréquence d'échantillonnage et résolution) qui permet d'approcher au mieux la réalité analogique.
La qualité des convertisseurs (et de l'horloge) permettra quant à elle d'une part de retranscrire au mieux la représentation du réel par des valeurs échantillonnées, et également de le faire au mieux dans l'ensemble de la plage de ses capacités (effets de bords liés au dépassement de certaines limites comme la saturation, jitter, sensibilité au bruit électromagnétique, etc.)
Je sors ça du fin fond de mes souvenirs, c'est peut-être pas très exact :bravo:

[ Dernière édition du message le 11/05/2018 à 23:25:08 ]

13
Citation de ChatNon :
Moi j'ai juste l'impression qu'un signal échantillonné en valeur fini ne peut jamais être parfaitement fidèle à un signal continu. Çà reste des approximations, plutôt très bonnes par ailleurs, mais des approximations, comme tout en numérisation.

Si tu vas par là, le simple fait d'amplifier un signal est une approximation car tu n'auras pas une fonction de transfert parfaitement linéaire dans un circuit électronique.
Par contre, tu prends un signal analogique, normalisé pour que la valeur de créte soit idéale pour un convertisseur donné.
Un convertisseur moderne ne quantifiera pas de la méme manière les modulations de faible amplitude que les modulations à plein échelle, justement afin réduire le bruit de quantification pour les signaux faibles.
Quand bien même ce convertisseur ne ferait "que" 16 bits, l'erreur sera tout à fait inaudible.

Un petit truc de formulation qui m'a beaucoup aidé lorsque j'ai été confronté à Shannon-Nyquist dans mes études.
Dire que le théorème prévoit une fréquence égale au moins au double de la fréquence maximale du signal n'est pas la formulation la plus correcte.
Une meilleure formulation, à mon point de vue, serait de dire que le théorème démontre qu'il n'y a aucune perte d'information si l'échantillonnage se fait à une fréquence au moins deux fois supérieure à la fréquence maximale contenant l'information qu'on veut discrétiser et que la reconstruction de ce signal (passage du domaine discret au domaine continu) se fera sans erreur.
En gros, si la discrétisation a été faite en respectant les critères de Shannon-Nyquist, on peut affirmer qu'il n'y a qu'une et une seule fonction passant par tous les points discrets et que cette fonction contient l'intégralité de l'information qui existait avant discrétisation.

Resistance is not futile... it's voltage divided by current

14
Tiens, je t'ai fait un petit exemple un peu pourrave.
Un son de 9 Hz (ligne rouge) et ce qu'il devient après numérisation à 20 Hz.
techniques-du-son-2241950.jpg
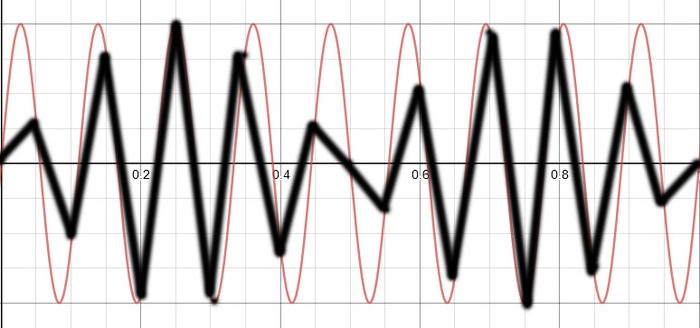
On peut pas dire que c'est fidèle. Le nombre de bit n'y changera rien. Le problème ne vient pas de la position verticale de chaque sommet de la ligne noire, mais du fait que ma grille verticale est grossière.

Néanmoins, les informations enregistrées doivent permettre (en théorie) de retrouver le signal initial.

[ Dernière édition du message le 11/05/2018 à 23:35:04 ]

15
AAb, tu dis: "Une meilleure formulation, à mon point de vue, serait de dire que le théorème démontre qu'il n'y a aucune perte d'information si l'échantillonnage se fait à une fréquence au moins deux fois supérieure à la fréquence maximale contenant l'information qu'on veut discrétiser et que la reconstruction de ce signal (passage du domaine discret au domaine continu) se fera sans erreur."

c'est là que je ne suis pas d'accord. Discrétiser, c'est perdre de l'information, qu'elle que soit la fréquence d’échantillonnage, si le signal d'origine est continu.
16
Le théorème de Shannon prétend seulement que tu peut prendre un nombre fini d'échantillons, fixés en fonction de la fréquence de Nyquist. mais les échantillons doivent être à valeurs réelles, pour une fidélité parfaite. Et si tu les discrétise, tu commences à perdre de l'information.
17
Citation de trazom :
Attention de ne pas en déduire qu'une fréquence de 4000 Hz permet d'enregistrer correctement tout ce qui est en dessous de 2000 Hz. Un signal de 1900 Hz, par exemple, va être sensiblement dégradé par un échantillonnage à 4000 Hz.


Si, c'est précisément ce que dit le théorème. On peut obtenir une reproduction parfaite d'un signal de fréquence strictement inférieure à la moitié de la fréquence d'échantillonnage.
En pratique, la raideur des filtres anti-repliement n'étant pas infinie, il faut garder un peu de marge entre la fréquence la plus haute du signal et Fe/2.
Mais pour reprendre ton exemple, une fréquence pure à 1.9kHz, qui ne bave absolument pas au-delà de 2kHz, peut être échantillonnée et parfaitement reproduite avec un échantillonnage à 4kHz.

Citation de trazom :
Un son de 9 Hz (ligne rouge) et ce qu'il devient après numérisation à 20 Hz.


Sauf que ton signal "résultat" contient plein de fréquences supérieures à la moitié de la fréquence d'échantillonnage. Filtre-les, et tu obtiendras une magnifique sinusoïde telle que tu avais mis au départ.

Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts

18
Citation de ChatNon :

c'est là que je ne suis pas d'accord. Discrétiser, c'est perdre de l'information, qu'elle que soit la fréquence d’échantillonnage, si le signal d'origine est continu.

Non, et c'est d'ailleurs le sujet de la démonstration de Shannon.

L'image que tu as postée est fausse.
Lorsqu'on reconstruit un signal discret, on relie pas les points entre eux par des segments de droite.
Renseigne-toi sur les bloqueurs d'ordre zéro et la transformée en Z.
Un petit rappel sur l'impulsion de Dirac et la fonction porte ne te ferait pas de mal non plus.

Resistance is not futile... it's voltage divided by current

19
Oui, c'est ce que je veux dire quand j'ajoute :
Citation :
Néanmoins, les informations enregistrées doivent permettre (en théorie) de retrouver le signal initial.
20
Je n'ai pas posté d'image
21
Citation :
Lorsqu'on reconstruit un signal discret, on relie pas les points entre eux par des segments de droite.

C'est pour ça que je disais que mon exemple est un peu pourrave.
Citation :
Renseigne-toi sur [...]
Un petit rappel sur l'impulsion [...] ne te ferait pas de mal non plus.

C'est obligatoire, ce ton ?
22
aab: tu dis
"Non, et c'est d'ailleurs le sujet de la démonstration de Shannon.

L'image que tu as postée est fausse.
Lorsqu'on reconstruit un signal discret, on relie pas les points entre eux par des segments de droite.
Renseigne-toi sur les bloqueurs d'ordre zéro et la transformée en Z.
Un petit rappel sur l'impulsion de Dirac et la fonction porte ne te ferait pas de mal non plus."

MOi je n'ai pas posté cette image, et je ne la valide pas.

23
@ChatNon: désolé, je n'ai pas fait attention que ce n'était pas toi qui avait posté cette image.

Resistance is not futile... it's voltage divided by current

24
Je dis "'est là que je ne suis pas d'accord. Discrétiser, c'est perdre de l'information, qu'elle que soit la fréquence d’échantillonnage, si le signal d'origine est continu.
aab : tu dis "Non, et c'est d'ailleurs le sujet de la démonstration de Shannon."

J'ai lu la démonstration de Shannon, il démontre l'équivalence d'un signal continu x(t) à valeur dans R avec un signal échantillonné à valeurs dans R.
25
Il faut faire attention. Il y a une grande différence entre la théorie mathématique et la réalité de l'enregistrement numérique. Dans la pratique, le signal se dégrade beaucoup lorsqu'on approche de la fréquence limite théorique (la moitié de la fréquence d'échantillonage). Mais mathématiquement, Shannon démontre bien que la donnée de cette échantillonnage permet de reconstituer exactement le signal original.