Théorème de Shannon.
- 103 réponses
- 12 participants
- 5 032 vues
- 20 followers
ChatNon
Je viens vous poster une question de mathématiques.
Le théorème d’échantillonnage de Shannon, qui prévoit une fréquence égale au moins au double de la fréquence maximale du signal est il résolu pour des valeurs d'échantillons appartenant à R (ensemble des nombres Réels) ou pour un ensemble fini comme 3 bits, ou 24 Bits par exemple?
je parle d’échantillonner un signal évidemment continu (audio).
Merci par avance,
Jimbass
c'est là que je ne suis pas d'accord. Discrétiser, c'est perdre de l'information, qu'elle que soit la fréquence d’échantillonnage, si le signal d'origine est continu.
Ce qu'il faut bien voir c'est que la "grille" amplitude-temps avec laquelle on quantifie le signal n'est absolument pas homogène. En prenant l'exemple du 16 bits/44.1 kHz, une période de signal audio sera décrite par 2 à 2205 échantillons. Mais chaque échantillon a 65536 valeurs possibles (et même 16 millions en 24 bits).
L'incertitude sur l'amplitude liée à la quantification est minuscule, comparée à l'erreur qui serait introduite par une fréquence d'échantillonnage imprécise (jitter).
Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts
ChatNon
Shannon, il démontre l'équivalence d'un signal continu x(t) à valeur dans R (ensemble des réels) avec un signal échantillonné à valeurs dans R. ( échantillonné suivant fréquence de Nyquist)
Il démontre également l’équivalence d'un signal discrétisé à valeur dans D (ensemble discret) avec un signal échantillonné à valeurs dans D. ( échantillonné suivant fréquence de Nyquist)
Mais Shannon ne démontre jamais l'équivalence d'un signal continu x(t) à valeur dans R avec un signal échantillonné à valeurs dans D. ( échantillonné suivant fréquence de Nyquist).
trazom
J'aurais dû préciser :
"Attention de ne pas en déduire qu'une fréquence de 4000 Hz permet d'enregistrer correctement tout ce qui est en dessous de 2000 Hz DANS LA PRATIQUE. Un signal de 1900 Hz, par exemple, va être EN REALITE sensiblement dégradé par un échantillonnage à 4000 Hz."
trazom
Mais Shannon ne démontre jamais l'équivalence d'un signal continu x(t) à valeur dans R avec un signal échantillonné à valeurs dans D. ( échantillonné suivant fréquence de Nyquist).
Absolument.
Sans m'avancer trop vite, je ne vois d'ailleurs pas trop comment ça pourrait être vrai.
Même si ton ensemble D est infini mais dénombrable, ça me parait difficilement possible.
[ Dernière édition du message le 12/05/2018 à 00:02:52 ]
Jimbass
Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts
trazom
trazom
Shannon ne nie pas l'existence d'un bruit de quantification, ce n'est tout simplement pas le sujet de ce théorème.
Oui, Shannon s'intéresse à la résolution temporelle. Tu sembles te questionner plutôt sur la profondeur de bit. Ce n'est pas vraiment l'objet de Shannon.
ChatNon
il y a combien de possibilités de sinusoïdes parfaites de fréquence comprises entre 50 hz et 20000 hz ? Une infinité non dénombrable.
En effet, il y a la fréquence 225. Mais également la 225,5, et la 225,57, puis 225,578...225,5789.....225,57893....
etc....225,578936785421359786123658... etc... une infinité de fréquences de sinusoïdes possibles.
Donc un signal x(t) continu ne peut être équivalent à un signal discret échantillonné.
trazom
Essaie d'enregistrer un signal avec une résolution de 44000 Hz mais avec seulement deux bits par échantillon. (donc 4 valeurs possibles).
Il est bien certain que, quelque soit la fréquence, il ne faut pas espérer une restitution fidèle d'un signal un peu complexe.
trazom
trazom
Ton exemple est bon, et rejoint mon histoire de cardinalité qui empêche la bijection.
Par contre, si tu retires de ta phrase "codé en 16 bits", l'argument ne fonctionne plus.
Donc Shannon a raison, et toi aussi.
[ Dernière édition du message le 12/05/2018 à 00:15:36 ]
ChatNon
Son théorème est parfaitement vrai...Dans son domaine de validité, comme tout théorème de mathématiques.
Desmodue
Après tout ces tripatouillages électroniques divers et variés, ce qui importe puisqu'on parle de sons à écouter, c'est justement l'écoute : si tu n'entends aucune différence entre le son brut et ce qui sort du convertisseur D/A inutile de se faire des noeuds au cerveau. Surtout si c'est pour en faire après des fichiers compressés.mp3 ou flac ou ogg ou... qui pour ce faire écrasent la dynamique et la bande passante, de façon assez astucieuse pour que ce soit plus ou moins inaudible.
trazom
[ Dernière édition du message le 12/05/2018 à 09:04:33 ]
EraTom
L'une des conséquences c'est que si la BANDE de fréquences du signal échantillonné fait la moitié de Fe, alors on peut le reconstruire sans erreur.
Pour un signal de bande plus large, il y a repliement et on ne peut plus reconstruire le signal.
Par exemple, si un signal est contenu dans une bande de 400Hz à 500Hz, de largeur 500-400=100Hz, alors il "suffit" d'échantillonner à 200Hz... Et c'est largement exploité dans les telecom.
Dans nos applications audio, la bande qui nous intéresse commence généralement à 0Hz, donc la largeur de bande correspond à la fréquence max du signal.
Le filtre d'antirepliement a un rôle de garde-fou pour se prémunir du problème de repliement ou de limiter le spectre à ce qui nous intéresse (en audio, ce que l'on entend).
Suffit entre guillemets parce que dans la vraie vie l'échantillonnage n'est pas réalisé de manière idéale :
- Le filtre n'est pas parfaitement raide, donc il faut mettre une marge ;
- Les Dirac ne sont pas parfaitement ponctuel ; on peut prédire l'effet en convoluant le signal échantillonné "parfait" avec la forme de l'impulsion "approximative", et on se rassure en s'apercevant que ça ne représente pas grand chose devant le reste.
ChatNon
Entre les fréquences 400hz et 500 hz, il n'y a pas 100 possibilités de fréquence, ni même 100 000 000, mais une infinité.
La théorie de l’échantillonnage peut prévoir de reconstituer une infinité de possibilité à la seule condition de stocker les valeurs réelles des échantillons, et non les valeurs approximatives sur 16 ou 24 bit.
Personne ne sait, ni ne saura JAMAIS stocker les valeurs réelles des échantillons d'un signal, car la majorité d'entre elles sont des valeurs irrationnelles.
Donc tout échantillon effectué en MAO est approximatif, et ne peut restituer qu'un nombre fini de possibilité de fréquence.
Si l'on considère l'ensemble infini des sinusoïdes parfaites d'amplitude µ, de fréquence comprise entre 20 hz et 20000 hz,
le format PCM 44.100*24 bit ne pourra en restituer qu'un nombre fini, que l'on doit pouvoir dénombrer qui plus est.
Ceci est valable également pour 96kzh*24 bit. Mais la question étant de savoir si on obtient le même nombre.
[ Dernière édition du message le 16/05/2018 à 01:53:28 ]
ChatNon
Donc à la question de savoir si le Théorème de Shannon, qui est un pur théorème de mathématiques, doit être suivi aveuglément lors de son application à des mesures physiques stockées dans des formats fini, je pense qu'il faut rester prudent.
Je ne conçois pas de convertisseurs audio, ni ne conçois de plugins pour Ozone ou l'Ircam. Eux mêmes sont en mesure de savoir les limitations pratiques de l'application de ce théorème de mathématiques.
Mais mon avis, qui n'engage que moi, est qu'il ne me semble pas aberrant qu'on puisse obtenir de meilleurs résultats en améliorant les résolutions d’échantillonnage, car on dispose dans tous les cas de plus d'informations sur le signal mesuré.
Jimbass
Tiens, je croyais que tu étais parti ...
Donc tout échantillon effectué en MAO est approximatif, et ne peut restituer qu'un nombre fini de possibilité de fréquence.
Oui, c'est vrai. Et alors ?
C'est une résolution très largement supérieure à celle que l'oreille est capable de percevoir.
il ne me semble pas aberrant qu'on puisse obtenir de meilleurs résultats en améliorant les résolutions d’échantillonnage
Mathématiquement oui, perceptuellement non.
Augmenter la résolution en amplitude réduirait le bruit de quantification. En 24 bits on est déjà à 144dB de dynamique ... et une oreille normalement constituée couvre 120dB entre le seuil d'audibilité et le seuil de douleur, à la fréquence la plus favorable qui plus est.
Augmenter la fréquence d'échantillonnage, ca se fait déjà, et avec des résultats très discutables : ca ne s'entend pas, mais ca permet de faire des filtres anti-repliement moins chers. Même en 44.1kHz on couvre correctement la bande audible par une oreille jeune et en bon état. (ce qu'on on ne doit pas être nombreux à avoir par ici ...)
Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts
ChatNon
Exemple: on peut stocker le nombre e (exponentielle) dans un manuel de mathématiques avec la fameuse formule:
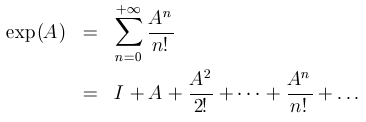
Jimbass
Ca y est, tu diverges.
Musikmesser 2013 - Bullshit Gourous - Tocxic Instruments - festivals Foud'Rock, Metal Sphère et la Tour met les Watts
[ Dernière édition du message le 16/05/2018 à 02:31:38 ]
ChatNon
Je vais pas rester longtemps, je fini ce que j'ai commencé.
Après pour le reste, moi je suis pas certain de qui a raison pour dire vrai, mais je sais que ceux qui brandissent des théorèmes de mathématiques en disant: "Ce sont les lois de l'audionumérique" comme si ils brandissaient l'évangile ont du sécher soit les cours de mathématiques, soit les cours de physiques.
[ Dernière édition du message le 16/05/2018 à 02:34:50 ]
ChatNon
Mais pour ce qui est du traitement audio-pro des fichiers, je ne trouverait pas aberrant qu'un mix traité tout du long en 96*24 puisse donner des meilleurs résultat qu'en 44.1*24.
Et encore, la différence peut être infime, je n'en sais rien. Cette question n'est pas si simple et ne peut être balayé d'un revers de la main: "Théorème de Shannon"
L'essentiel dépend du mixer et de ses sources.
Dr Pouet
Si on fait une analogie avec le cinéma, la fréquence d’échantillonnage est le nombre d’image par seconde, et le pas de quantification est le nombre de pixels par image. Les deux sont totalement indépendants. Le théorème de Shannon porte sur la fréquence d’échantillonnage, pas sur le pas de quantification.
Cf post 6 :
https://fr.audiofanzine.com/techniques-du-son/forums/t.665377,theoreme-de-shannon,post.9625771.html
[ Dernière édition du message le 16/05/2018 à 02:47:16 ]
ChatNon
Vous mélangez tout.
[ Dernière édition du message le 16/05/2018 à 02:46:50 ]
ChatNon
je ne saurai comment vous faire désapprendre.
Donc restons en là.
Ce débat sera stérile.
- < Liste des sujets
- Charte
