réactions au dossier [Bien débuter] À haute fréquence (ou pas...)
- 79 réponses
- 17 participants
- 11 557 vues
- 20 followers
Anonyme
trazom
Citation :
Et oui, trigo de 4ème :p
miles1981
Ben oui, je sais, mais j'avais jamais vu la représentation des harmoniques...
Oui, c'est vrai que c'est sympa
Audio Toolkit: http://www.audio-tk.com/
Choc
newjazz
*Seed*
Le sinus a toujours été le rapport côté opposé sur hypothénus. Avec un hypothénus à 1 (rayon du cercle), on a directement la fonction sinus (et cosinus) lorsque tu fais faire un cercle à ton point.
je suis pas vraiment une flêche en maths (j'ai un bac L) par contre ta phrase là c'est pas du français....tout simplement incompréhensible....
Sysex and sun
trazom
C'est de la géométrie... pas facile à expliquer par écrit, quoi...
Avec un petit dessin, c'est beaucoup plus clair :
*Seed*
Sysex and sun
trazom
Je relève le défi :
PARTIE 1 : le sinus d'un angle (programme de 3ème)
Observons un triangle rectangle :
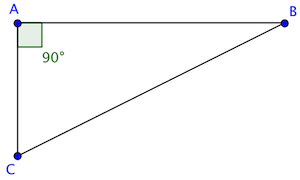
Si je regarde l'angle B, on peut dire que le côté AC lui est opposé.
BC s'appelle l'hypoténuse, car il est opposé à l'angle droit.
Si je multiplie l'hypoténuse par un coefficient, je trouve le côté opposé.
Par exemple, si l'hypoténuse mesure 10 cm et le côté opposé 6 cm, j'ai :
hypoténuse*0,6=opposé.
Ce qui est remarquable, c'est que ce coefficient ne dépend que de la mesure de l'angle B, et pas des dimensions choisies pour le triangle.
En ce sens, il est caractéristique de l'angle B. C'est pourquoi on lui donne un nom : SINUS de l'angle B.
Le 0,6 de mon exemple correspond par exemple forcément à un angle de 37°.
Le SINUS, c'est "par combien je dois multiplier l'hypoténuse pour trouver le côté opposé".
Si tu le connais, la calculette te diras combien mesure l'angle.
Je peux continuer si ça intéresse quelqu'un.
Non ?
Et la musique la dedans ? euh...
EraTom
1) Trace un repère (O,x,y) : Deux axes perpendiculaires avec x horizontal et y vertical qui se coupe au point O (l'origine du repère).
2) Trace un cercle de rayon 1 dont le centre est O.
3) Place un point M sur le cercle. On note "a" l'angle entre l'axe des x et le segment [om]. Prend M tel que "a" soit entre 0° et 90° (les coordonnées de M(xm;ym) sont positives ou nulles).
Trace le segment [om] qui est un rayon du cercle (sa longueur est donc de 1).
4) Tire un trait vertical (parallèle à l'axe y) qui va de M jusqu'à l'axe des x ; on va noter P le point d'intersection entre ce trait vertical et l'axe des x.
Maintenant on regarde ce que l'on a sur ce schéma :
- Le segment [op] a un longueur qui représente la coordonnée xm de M suivant les abscisses x ;
- Le segment [pm] a un longueur qui représente la coordonnée ym de M suivant les ordonnées y ;
- Le triangle OPM est un triangle rectangle en P, son hypoténuse est [om] (de longueur 1).
Dans ce triangle rectangle tu peux calculer (en n'oubliant pas que [om] = 1) :
- Le cosinus de a : cos(a) = [op] / [om] = [op]/1 = [op] = xm
- Le sinus de a : sin(a) = [pm] / [om] = [mp]/1 = [mp] = ym
Donc en prenant un point M sur un cercle de rayon 1 centré en O on obtient un point dont les coordonnées sont les cosinus et sinus de l'angle "a" entre l'axe des x est [om] : M(xm;ym) = M(cos(a);sin(a))
C'est ce que l'on appelle le cercle trigonométrique.
C'est ce qui est illustré sur ce schéma :
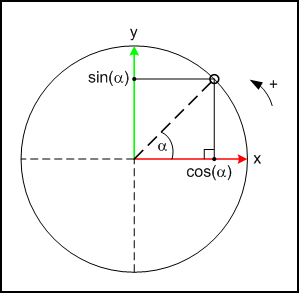
Pour les autres quarts du cercle ("a" plus grand que 90°) ça marche aussi, exactement suivant le même raisonnement, mais il faut mettre des signes sur les distances des segments [pm] et [op] pour que ça correspondent aux coordonnées de M..
[ Dernière édition du message le 07/03/2015 à 16:43:40 ]
- < Liste des sujets
- Charte