réactions au dossier [Bien débuter] Quel format d’enregistrement ?
- 249 réponses
- 55 participants
- 35 898 vues
- 63 followers
Nantho Valentine
Lire l'article
Ce thread a été créé automatiquement suite à la publication d'un article. N'hésitez pas à poster vos commentaires ici !
miles1981
Cela dit, il semblerait que techniquement ça ne soit pas possible d'avoir 32 bits significatif, même pour 24 bit significatif c'est pas clair (à ma connaissance). C'est à dire que les bits supplémentaires ne code pas du son, mais du bruit.
Par contre en N/A pour l'audio je vois pas ce que ça apporterai.
Yep, on n'est pas encore a 144dB (en fait, c'est un poil moins) pour le bruit d'un convertisseur haut de gamme.
Audio Toolkit: http://www.audio-tk.com/
miles1981
Non, les fréquences négatives n'ont aucun sens. C'est le théorème de Nyquist qui dit que si tu veux encoder un signal jusque 20kHz, il faut échantillonner au moins à 40kHz (fréquence x 2).
Ensuite, la marge (de 40kHz à 44.1kHz ou 48kHz) te donne la pente du filtre anti-repliement.
Et pourtant si, ca a du sens. C'est la realite qui est justement due au theoreme de Shannon-Nyquist. C'est d'ailleurs pour ca que le theoreme n'est pas limite aux frequences "graves", mais bien a une bande passnate et qu'on pourrait aussi filtrer et selectionner un signal qui serait autour de 1MHz.
Quand on echantillonne, on replie le spectre. Ce qui est replie, dans le domaine spectral, c'est bien 44.kHz de frequences. Un signal real a des frequences positives et negatives qui sont symetriques. Et c'est ce sont ces frequences negatives qui se retrouvent repliees au-dela de Nyquist et qui posent probleme si la pente des filtres anti-repliement n'est pas assez forte par rapport a la largeur de la bande inaudible qui reste.
Audio Toolkit: http://www.audio-tk.com/
[ Dernière édition du message le 02/05/2019 à 18:27:24 ]
trazom
Et pourtant si, ca a du sens.
Disons que ça n'a pas de sens physique. Les fréquences négatives, c'est plutôt une abstraction mathématique.
Et j'ai l'impression que le terme est beaucoup plus utilisé dans le monde de l'électronique.
Danbei
Non, les fréquences négatives n'ont aucun sens. C'est le théorème de Nyquist qui dit que si tu veux encoder un signal jusque 20kHz, il faut échantillonner au moins à 40kHz (fréquence x 2).
On peut même interpréter l'idée des fréquences négatives : What is the physical significance of negative frequencies?.
Par contre, dans le cas de l'audio numérique, effectivement ça n'a pas l'air d'avoir du sens.
trazom
Prenons un signal de 1 Hz.
Il se répète identiquement une fois par seconde :
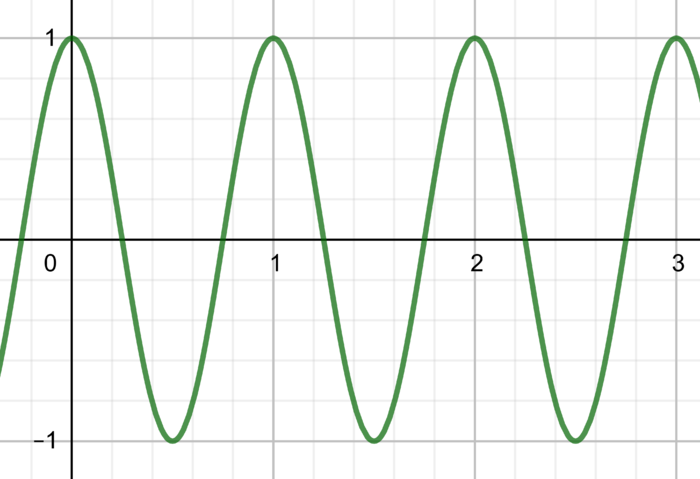
Je veux l'enregistrer. Je vais donc l'échantillonner, c'est à dire regarder la position des points de la ligne verte. Comme il y en a une infinité, je ne vais en prendre qu'un seul par seconde : J'enregistre à 1 Hz.
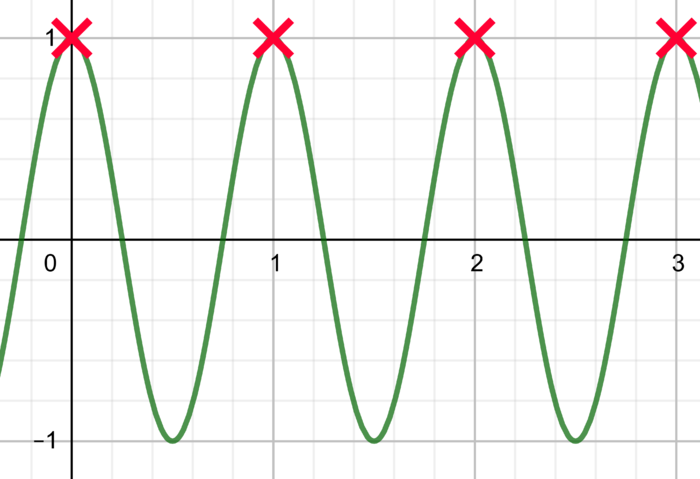
Voici ce qu'il reste après enregistrement : le signal numérisé :

Bon, on est d'accord pour dire que je vais avoir du mal à retrouver le signal de départ avec ça.
Il me faut plus de points.
Je vais donc maintenant échantillonner à 2 Hz, c'est à dire que je vais prendre deux points du signal chaque seconde :
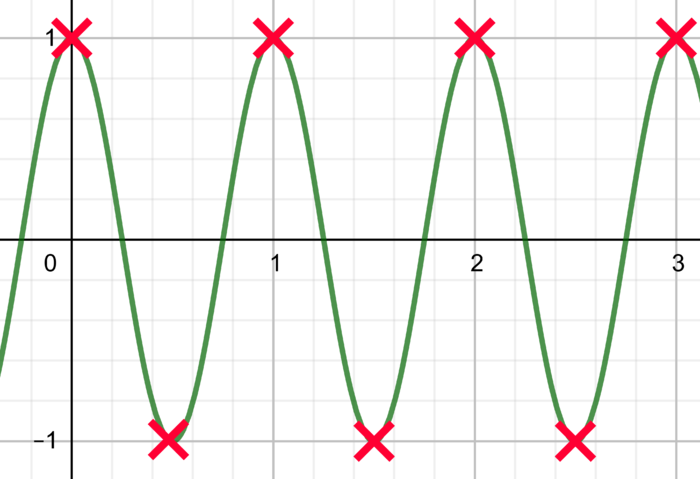
Voici le signal numérisé :

Et je peux jouer à relier les points pour commencer à retrouver le signal d'origine :
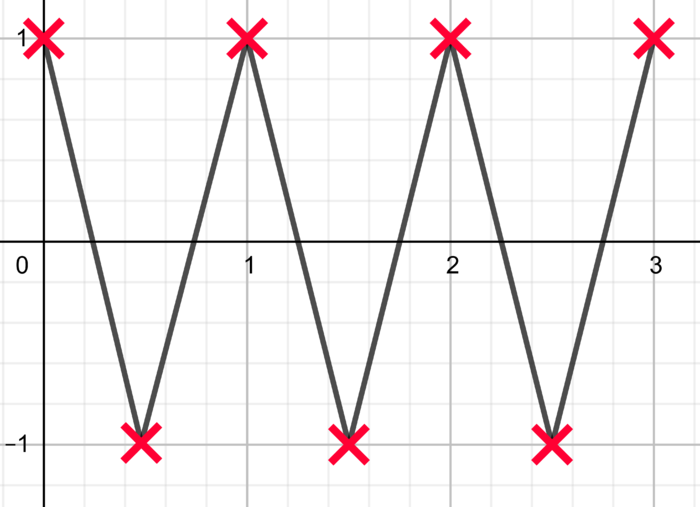
Ca commence à ressembler beaucoup plus à mon signal de départ.
Maintenant, un peu de théorie :
Ce que dit le théorème de Shannon, et qui est assez extraordinaire, c'est en fait que les points rouges que je viens d'enregistrer permettent de reconstituer exactement le signal de départ, à condition d'avoir enregistré avec une fréquence au moins deux fois supérieure à la fréquence du signal.
Mon signal étant de 1 Hz, et mon échantillonnage de 2 Hz, j'ai l'assurance de retrouver exactement mon signal de départ.
Le théorème s'étend à un signal beaucoup plus complexe qu'une sinusoïde, bien sûr.
trazom
[ Dernière édition du message le 02/05/2019 à 23:04:16 ]
Will Zégal
Après, les STAN font souvent des calculs en 32 bits flottants (c'est à dire un format de nombre permettant des virgules ou des exposants, donc avec une grande marge de grandeur), voire en 64 bits, ce qui permet notamment d'éviter l'écrêtage si on dépasse le 0 dBFS temporairement, par exemple à l'intérieur d'une disto dont on aurait baissé le niveau de sortie, mais qui reçoit un signal qui monte à plus de 0 dB pendant le traitement.
C'est ça qui permet, même si ce n'est pas recommandé, d'avoir des pistes individuelles qui "tapent dans le rouge" sans forcément avoir de saturation numérique sur la sortie générale.
Par contre en N/A pour l'audio je vois pas ce que ça apporterait
du marketing. On en a parlé dans "les gri-gris en hifi", mais Sony vient d'annoncer ou de sortir un baladeur idiophile proposant de gérer du DSD ou des FE et bits de quantification de dingue. Les gogos qui achèteront ça ne trouveront probablement aucun fichier à ces standards pour nourrir leur bestiau, mais il y en aura certainement plein à penser que "qui peut le plus fait mieux le moins" et ce n'est pas impossible que Sony, major du disque, ait trouvé là le moyen à terme de revendre encore une fois à prix d'or les catalogues amortis déjà vendus en vinyl, puis en CD, puis en mp3, puis en HD chez Qubuz...
Louis Armstrong en 384 kHz, ça change tout
[ Dernière édition du message le 02/05/2019 à 23:18:52 ]
Gooliver7
ce n'est pas impossible que Sony, major du disque, ait trouvé là le moyen à terme de revendre encore une fois à prix d'or les catalogues amortis déjà vendus en vinyl, puis en CD, puis en mp3, puis en HD chez Qubuz...
ce qui est drôle c'est que ces derniers temps on a assisté parfois à une compression de la qualité audio avec la culture du mp3, spotify.. etc...
maintenant si on nous parle de audio HD des bits et des fréquences d échantillons élevés...ça va un peu dans l'autre sens!
bonjour nos disque durs!
https://www.youtube.com/user/gooliver7
Anonyme
Ce que dit le théorème de Shannon, et qui est assez extraordinaire, c'est en fait que les points rouges que je viens d'enregistrer permettent de reconstituer exactement le signal de départ, à condition d'avoir enregistré avec une fréquence au moins deux fois supérieure à la fréquence du signal.
Mon signal étant de 1 Hz, et mon échantillonnage de 2 Hz, j'ai l'assurance de retrouver exactement mon signal de départ.
Le théorème s'étend à un signal beaucoup plus complexe qu'une sinusoïde, bien sûr.
Oui, et du coup il faut OUBLIER toutes les représentations en lignes brisées ou marches d'escalier, qui n'ont AUCUN sens et qui ne représentent pas du tout ce qu'il se passe en réalité.
trazom
je peux jouer à relier les points pour commencer à retrouver le signal d'origine
Ce que dit le théorème de Shannon, et qui est assez extraordinaire, c'est en fait que les points rouges
miles1981
On peut ajouter qu'en 32 bits, la quantité de données à traiter, stocker, lire, mettre en mémoire, calculer, etc augmente considérablement, donc consomme beaucoup de ressource sans que ça ait un intérêt certain pour l'audio.
Faut préciser quand tu parles de virgule fixe et flottante !
Audio Toolkit: http://www.audio-tk.com/
Danbei
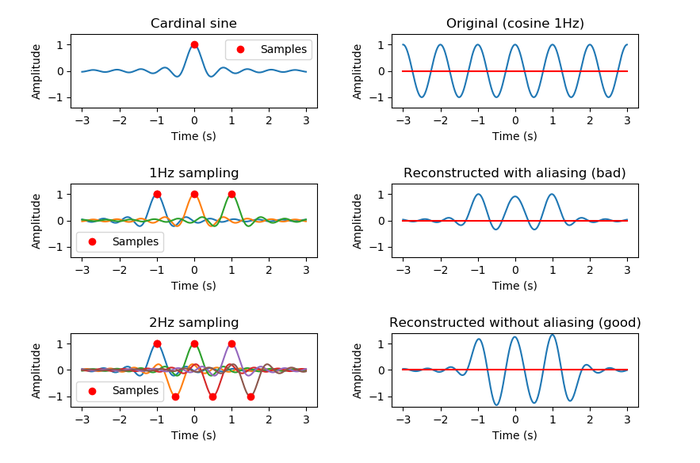
Oui, et du coup il faut OUBLIER toutes les représentations en lignes brisées ou marches d'escalier, qui n'ont AUCUN sens et qui ne représentent pas du tout ce qu'il se passe en réalité.
Une illustration sans lignes brisées, avec des jolie courbes :
- Première ligne :
- Deuxième ligne : Echantillonnage à 1 Hz.
- Troisième ligne : Echantillonnage à 2 Hz.
EraTom
En principe il faut échantillonner pendant un temps infini, en pratique il faut échantillonner pendant un temps "suffisant".
Si l'on applique ses deux transformations au signal continu (multiplication par une fonction porte pour le prélèvement puis produit de convolution par un sinc pour le filtrage) pour modéliser ce qu'il se passe en "vrai" pour le signal analogique avant échantillonnage, on retrouve bien la même chose que la reconstruction numérique.
[ Dernière édition du message le 09/05/2019 à 08:22:55 ]
CuriousSam
J'ai lu l'article et je me pose encore des questions. Premièrement, comment pourrait-on définir une plage dynamique ? Parce que je suis venu avec cette recherche. J'ai un micro avec une plage dynamique de 120 dB (micro cravate sans fil) et je n'arrive pas à savoir à quoi ça correspond, si c'est bon ou pas etc.
Dans l'article il est écrit :
Cela peut paraître amplement suffisant pour une production moderne puisque les plus dynamiques d’entre elles présentent un écart de volume entre le passage le plus fort et le passage le plus faible de seulement 18 dB tout au plus.
Donc ça laisse à penser que le signal utile doit au moins être de 18 dB pour comprendre le son le plus fort et le plus faible. Une démonstration nous amène à 76 dB avec le bruit de fond et le pic à 0 dB ( que je n'ai pas compris, sur le dessin il est au-dessus, mais il est à 0 dB c'est surprenant ). Donc 76 dB ça comprend largement 18 dB alors pourquoi passer à 24 bits ? La démonstration ne m'a pas convaincu, mais c'est surtout que je n'ai pas compris en fait.
Peut-être une piste ici :
il est toutefois primordial d’avoir une captation la plus proche possible de la source afin de conserver une belle marge de manœuvre lors des étapes ultérieures.
Mais je ne sais pas de quelles étapes on parle donc de quelle marge parle-ton.
Merci pour votre aide qui me sera précieuse ici.
Danbei
J'ai lu l'article et je me pose encore des questions. Premièrement, comment pourrait-on définir une plage dynamique ?
Dans l'article il est écrit :Citation :Cela peut paraître amplement suffisant pour une production moderne puisque les plus dynamiques d’entre elles présentent un écart de volume entre le passage le plus fort et le passage le plus faible de seulement 18 dB tout au plus.
Donc ça laisse à penser que le signal utile doit au moins être de 18 dB pour comprendre le son le plus fort et le plus faible. Une démonstration nous amène à 76 dB avec le bruit de fond et le pic à 0 dB ( que je n'ai pas compris, sur le dessin il est au-dessus, mais il est à 0 dB c'est surprenant ). Donc 76 dB ça comprend largement 18 dB alors pourquoi passer à 24 bits ? La démonstration ne m'a pas convaincu, mais c'est surtout que je n'ai pas compris en fait.
- S'il y a 18 dB entre la partie la plus forte et la moins forte d'un morceau, on veut pouvoir reproduire la partie faible sans entendre le bruit de fond du convertisseur. Donc le bruit de fond du convertisseur doit être significativement en dessous du niveau le plus faible. Le convertisseur doit donc avoir une dynamique significativement plus grande que 18 dB.
- 18 dB c'est la dynamique à la fin de la production. A l'enregistrement la dynamique peut être plus grande, 40 dB par exemple. Donc il faut que le convertisseur ait une dynamique significativement plus grande que 40 dB. L'article fait référence à cela.
- Enfin, on ne sait pas à l'avance quel sera le niveau le plus haut de ce qu'on enregistre, il faut donc se donner une marge au cas ou le niveau est plus haut que ce que l'on avait anticipé, par exemple 15 dB. Il faut donc que le convertisseur ait une dynamique significativement plus grande que 40 dB + 15 dB = 55 dB.
Dans certains cas 16 bits ne sont pas suffisant parce que la dynamique de ce qu'on enregistre est plutôt grande (deuxième point) ou parce que il y a une grande incertitude sur le niveau maximal (troisième point).
C'est toujours plus confortable avec 24 bits, ça permet notamment de se donner une marge (le troisième point) encore plus grande et de ne pas avoir a trop réfléchir aux niveaux.
laurend
Comme on parle ici musique, je préfère réserver l'usage du mot dynamique à la description de la différence entre le niveau moyen et le niveau maximal des crêtes.
MaximalSound.com
Le mastering algorithmique en ligne depuis 2010
Démo SoundCloud
Sound On Sound Shootout
Crédits YouTube
VE
Nantho Valentine
VE
Nantho Valentine
rroland
Will Zégal
rroland
En fait, "les oreilles non averties " ça couvre un spectre assez large
Oui, cela couvre le monde entier, sauf les ingés-son et les bons musiciens
J'utilise mon épouse ou mon fils. Ils n'entendent rien
[ Dernière édition du message le 10/04/2021 à 17:08:07 ]
Danbei
laurend
ils disent "j'aime pas", quand un habitué pourra analyser et préciser ce qui cloche
+1
MaximalSound.com
Le mastering algorithmique en ligne depuis 2010
Démo SoundCloud
Sound On Sound Shootout
Crédits YouTube
- < Liste des sujets
- Charte

