réactions au dossier [Bien débuter] Quel format d’enregistrement ?
- 249 réponses
- 55 participants
- 34 230 vues
- 63 followers
Afficher le sujet de la discussion
Will Zégal
75428
Will Zégal
Membre depuis 22 ans
Je crois qu'il existe des convertisseurs 32 bits. Mais surtout en DA.
Je ne suis pas convaincu de l'intérêt de 32 bits en AD, en tous cas pour la musique. En 16 bits, tu disposes déjà de 96 dB de dynamique.
Sachant que la plupart des conditions d'écoute sont dans des environnements ayant au moins 20-25 dB de bruit de fond (standard d'un studio d'enregistrement, c'est à dire plus calme qu'une maison à la campagne tant qu'il reste quelques oiseaux), ça veut dire que si tu utilises toute cette dynamique avec les sons les plus faibles à 25 dB, les sons les plus forts seront à 121 dB. C'est un peu fort
Sachant que les conditions d'écoute classiques sont plutôt dans 40 dB de bruit de fond (une chambre la nuit en ville), tu aurais en 16 bits des crêtes à 136 dB, soit le volume d'un réacteur d'avion.
Sachant que la plupart des disques du commerce ont une dynamique réelle autour d'une quinzaine de décibels, une vingtaine au mieux.
en 24 bits, tu as une dynamique de 144 dB. Autant te dire que t'es pas prêt de l'exploiter sur un titre de musique, pour peu que tu aies un système de diffusion capable de rendre une telle dynamique (différence entre bruit de fond et volume max). Sachant aussi que je ne vois pas beaucoup de micros qui disposent d'une telle dynamique.
Donc, ça ne sert à rien, en tous cas pour de l'audio musical (ça peut être autre chose dans le domaine scientifique, j'imagine), d'avoir des convertisseurs 32 bits. Avec 24 bits, tu es déjà au delà de la dynamique offerte par les systèmes analogiques tant en enregistrement qu'en restitution et très très au delà de l'usage pratique.
Je ne suis pas convaincu de l'intérêt de 32 bits en AD, en tous cas pour la musique. En 16 bits, tu disposes déjà de 96 dB de dynamique.
Sachant que la plupart des conditions d'écoute sont dans des environnements ayant au moins 20-25 dB de bruit de fond (standard d'un studio d'enregistrement, c'est à dire plus calme qu'une maison à la campagne tant qu'il reste quelques oiseaux), ça veut dire que si tu utilises toute cette dynamique avec les sons les plus faibles à 25 dB, les sons les plus forts seront à 121 dB. C'est un peu fort
Sachant que les conditions d'écoute classiques sont plutôt dans 40 dB de bruit de fond (une chambre la nuit en ville), tu aurais en 16 bits des crêtes à 136 dB, soit le volume d'un réacteur d'avion.
Sachant que la plupart des disques du commerce ont une dynamique réelle autour d'une quinzaine de décibels, une vingtaine au mieux.
en 24 bits, tu as une dynamique de 144 dB. Autant te dire que t'es pas prêt de l'exploiter sur un titre de musique, pour peu que tu aies un système de diffusion capable de rendre une telle dynamique (différence entre bruit de fond et volume max). Sachant aussi que je ne vois pas beaucoup de micros qui disposent d'une telle dynamique.
Donc, ça ne sert à rien, en tous cas pour de l'audio musical (ça peut être autre chose dans le domaine scientifique, j'imagine), d'avoir des convertisseurs 32 bits. Avec 24 bits, tu es déjà au delà de la dynamique offerte par les systèmes analogiques tant en enregistrement qu'en restitution et très très au delà de l'usage pratique.
Will Zégal
75428
Will Zégal
Membre depuis 22 ans
Gooliver7
1120
AFicionado·a
Membre depuis 22 ans
Danbei
1892
AFicionado·a
Membre depuis 13 ans
alex.d.
5571
Je poste, donc je suis
Membre depuis 9 ans
miles1981
8360
Je poste, donc je suis
Membre depuis 20 ans
miles1981
8360
Je poste, donc je suis
Membre depuis 20 ans
trazom
1819
AFicionado·a
Membre depuis 20 ans
Danbei
1892
AFicionado·a
Membre depuis 13 ans
trazom
1819
AFicionado·a
Membre depuis 20 ans
Je tente une explication sans parler de Fourier/Shannon/Nyquist...
Prenons un signal de 1 Hz.
Il se répète identiquement une fois par seconde :
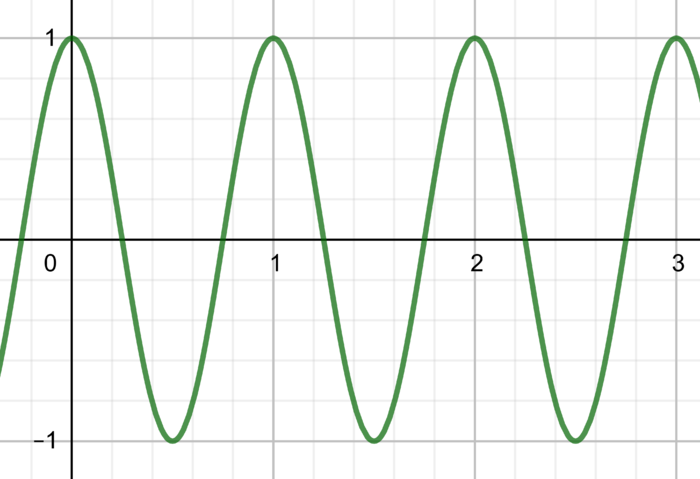
Je veux l'enregistrer. Je vais donc l'échantillonner, c'est à dire regarder la position des points de la ligne verte. Comme il y en a une infinité, je ne vais en prendre qu'un seul par seconde : J'enregistre à 1 Hz.
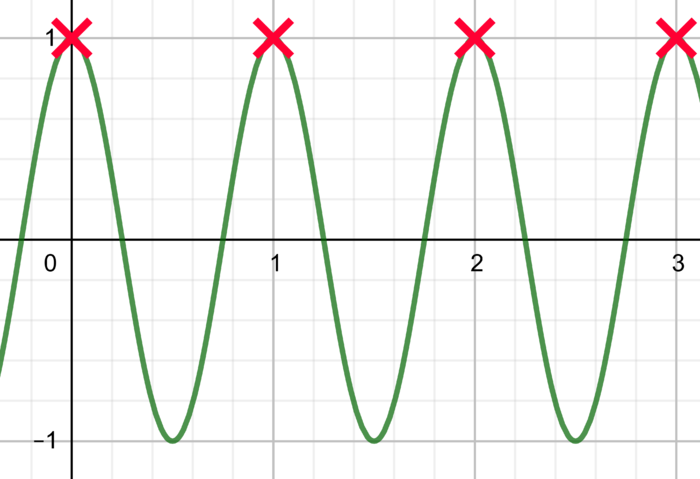
Voici ce qu'il reste après enregistrement : le signal numérisé :
Bon, on est d'accord pour dire que je vais avoir du mal à retrouver le signal de départ avec ça.
Il me faut plus de points.
Je vais donc maintenant échantillonner à 2 Hz, c'est à dire que je vais prendre deux points du signal chaque seconde :
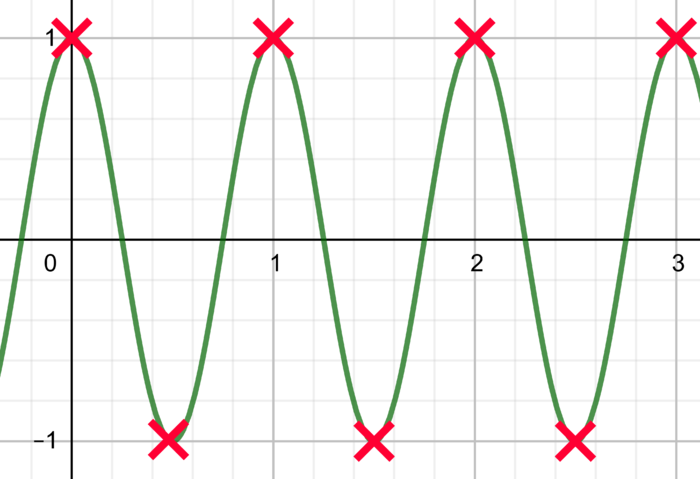
Voici le signal numérisé :
Et je peux jouer à relier les points pour commencer à retrouver le signal d'origine :
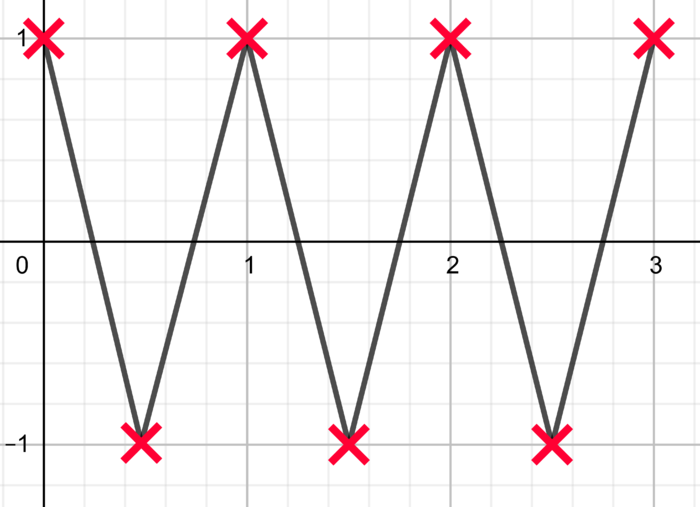
Ca commence à ressembler beaucoup plus à mon signal de départ.
Maintenant, un peu de théorie :
Ce que dit le théorème de Shannon, et qui est assez extraordinaire, c'est en fait que les points rouges que je viens d'enregistrer permettent de reconstituer exactement le signal de départ, à condition d'avoir enregistré avec une fréquence au moins deux fois supérieure à la fréquence du signal.
Mon signal étant de 1 Hz, et mon échantillonnage de 2 Hz, j'ai l'assurance de retrouver exactement mon signal de départ.
Le théorème s'étend à un signal beaucoup plus complexe qu'une sinusoïde, bien sûr.
Prenons un signal de 1 Hz.
Il se répète identiquement une fois par seconde :
Je veux l'enregistrer. Je vais donc l'échantillonner, c'est à dire regarder la position des points de la ligne verte. Comme il y en a une infinité, je ne vais en prendre qu'un seul par seconde : J'enregistre à 1 Hz.
Voici ce qu'il reste après enregistrement : le signal numérisé :
Bon, on est d'accord pour dire que je vais avoir du mal à retrouver le signal de départ avec ça.
Il me faut plus de points.
Je vais donc maintenant échantillonner à 2 Hz, c'est à dire que je vais prendre deux points du signal chaque seconde :
Voici le signal numérisé :
Et je peux jouer à relier les points pour commencer à retrouver le signal d'origine :
Ca commence à ressembler beaucoup plus à mon signal de départ.
Maintenant, un peu de théorie :
Ce que dit le théorème de Shannon, et qui est assez extraordinaire, c'est en fait que les points rouges que je viens d'enregistrer permettent de reconstituer exactement le signal de départ, à condition d'avoir enregistré avec une fréquence au moins deux fois supérieure à la fréquence du signal.
Mon signal étant de 1 Hz, et mon échantillonnage de 2 Hz, j'ai l'assurance de retrouver exactement mon signal de départ.
Le théorème s'étend à un signal beaucoup plus complexe qu'une sinusoïde, bien sûr.
- < Liste des sujets
- Charte