Après avoir vu les bases théoriques dans la première partie du dossier consacrée aux formes d’ondes, nous allons, dans cette seconde partie, nous plonger dans le concret.
Une onde complexe, susceptible d’être intéressante sur un plan musical, peut être obtenue de plusieurs façons. Pour l’instant, on se contentera de simplement développer cette idée d’addition d’harmoniques telle qu’elle a été abordée dans les chapitres précédents.
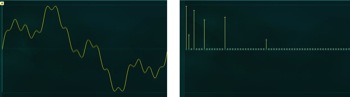
La vidéo de la première partie a montré comment l’ajout d’harmoniques permettait de complexifier le son, mais nous obtenions un résultat désagréable à l’oreille. Ceci était lié au fait que les harmoniques avaient été réglées totalement au hasard.
Mettons un peu d’organisation dans la distribution des harmoniques sur une idée très simple :
-
N’activons que les harmoniques qui coïncident avec les octaves, à savoir les harmoniques de rang 1, 2, 4, 8, 16, 32…
-
et dosons les amplitudes de ces seules harmoniques
Au final, la texture générale du son obtenu rappelle celle d’un orgue. Rien d’étonnant à cela, car les tirettes d’un orgue Hammond (les drawbars) agissent justement sur l’amplitude des harmoniques. C’est tout de même plus pratique que de devoir viser quelques pixels avec une souris:

Ce principe est également émulé dans certains instruments actuels comme le Nord Electro de Clavia:

Une conclusion semble s’imposer : pour créer un son, le hasard peut être intéressant en découvertes, mais un minimum de connaissance des phénomènes acoustiques permet de construire des sons dans un objectif précis qu’on s’est fixé. Ceci sera confirmé au fur et à mesure qu’on découvrira l’ensemble des modules qui composent un instrument. La distribution plus ou moins organisée des harmoniques nous permet maintenant de développer encore d’autres formes d’ondes, et ceci, dans un but musical.
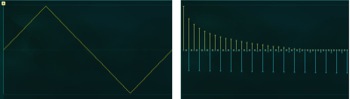
Forme triangle
La forme d’onde est le premier paramètre à choisir lors de la création d’un son synthétique et est primordiale sur le résultat final. Pour rappel, voici la forme d’onde et le spectre du son d’orgue :
L’onde suit une courbe douce, sans angle vif ni ligne droite : peu d’harmoniques sont en jeu. L’obtention d’angles vifs et de lignes droites nécessite un grand nombre de sinusoïdes élémentaires : ces formes d’ondes sont donc riches en harmoniques. Notons que c’est la loi de Fourier, à l’origine de l’étude de la conduction thermique, qui définit cette superposition de sinusoïdes des ondes sonores complexes. Comme exemple voici la forme d’onde triangle et son spectre harmonique :
Les harmoniques sont distribuées de façon précise et répondent à un schéma particulier. Afin de contraindre la forme d’onde à suivre une ligne droite, il est nécessaire que certaines harmoniques soient plus ou moins déphasées par rapport à la fondamentale, ce qui s’observe grâce aux barres bleues dirigées vers le bas. Si nécessaire, voici une illustration de la notion de phase : à gauche, une onde en phase (elle commence à la valeur zéro), et à droite elle est hors phase (elle commence à une valeur différente de zéro) :
Voici le son obtenu par une onde triangle
On dit d’une telle sonorité qu’elle est flûtée. Sans entrer dans des certitudes scientifiques, il est intéressant de se demander pour quelle raison une onde triangle ressemble plus ou moins au son d’une flûte. Pour cela, commençons par observer la forme d’onde réelle d’une flûte, et en particulier sa ressemblance avec une onde triangulaire :

Si elle est plus complexe que le modèle quasiment parfait présenté précédemment, c’est qu’interviennent un certain nombre de phénomènes physiques qui s’ajoutent à la seule création de l’onde par le souffle de l’instrumentiste. Il s’agit des aspérités à l’intérieur de l’instrument, des matériaux qui ont leur propre résonance, etc. Mais l’essentiel du son est produit par le souffle. Il faut garder en mémoire que l’intérieur de la flûte est un cylindre plus ou moins clos et que si on y insuffle de l’air sous pression, cet air s’échappera de l’autre côté de l’instrument. Le son est produit car l’air ne s’échappe pas de façon régulière (ce qui ne produirait pas d’oscillation acoustique), mais de la manière suivante :
-
Le souffle augmente progressivement la quantité d’air dans l’instrument
-
La pression augmente progressivement (c’est la ligne droite ascendante de l’onde)
-
L’air commence à s’échapper et la quantité d’air diminue
-
La pression diminue progressivement (ligne droite descendante)
-
Le souffle continue à alimenter l’instrument en air et la pression augmente à nouveau
Et ainsi de suite, ce cycle se répétant 440 fois par seconde lorsque l’instrumentiste joue un La. Cette description est évidemment schématique, mais représente assez bien la relation entre la forme d’onde, le phénomène physique et le résultat auditif. On peut tenter de procéder à l’inverse : partir d’un instrument et s’interroger sur la forme d’onde simplifiée qui pourrait le caractériser en précisant le phénomène physique qui l’expliquerait.
Forme dent de scie
 Dans la famille des instruments à cordes frottées, le principe de la production du son repose sur l’important coefficient de frottement entre le crin de l’archer et la corde :
Dans la famille des instruments à cordes frottées, le principe de la production du son repose sur l’important coefficient de frottement entre le crin de l’archer et la corde :
-
Lorsque l’instrumentiste balaie la corde de son archer, l’adhérence entre les deux matériaux en contact va créer une traction radiale sur la corde jusqu’à un certain seuil où l’adhérence n’est plus suffisante pour maintenir ce contact,
-
Dès la perte d’adhérence, le son est immédiatement produit à une amplitude maximale (passage instantané de zéro au maxi, représenté par une ligne droite verticale sur le dessin de la forme d’onde),
-
Pour ensuite revenir progressivement au silence (ligne droite descendante),
-
Retour d’adhérence et un nouveau cycle recommence.
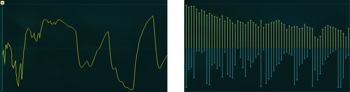
Ce cycle se répète 440 fois par seconde lorsque l’instrumentiste joue un La. Donc attention, on parle bien de la forme d’onde une fois la note tenue et stabilisée, et non de l’enveloppe générale du timbre qui ferait intervenir le son de l’attaque puis celui du maintien. La forme d’onde ainsi décrite est appelée dent de scie par analogie avec les dents d’une scie lorsque l’on trace plusieurs ondes successives.
Le spectre a ceci de particulier que les harmoniques sont toutes présentes et perdent leur amplitude au fur et à mesure qu’on augmente dans les fréquences sans cependant s’éteindre entièrement (la figure ne montre que les 64 premières harmoniques, mais on peut facilement extrapoler la suite). La forme d’onde en dent de scie comporte une infinité d’harmoniques. On se souvient, lors du premier chapitre que
-
Plus une onde suit une courbe douce, moins elle est formée d’harmoniques (le cas extrême étant l’onde sinusoïdale, la plus douce de toutes les courbes, qui n’est formée que de la fondamentale),
-
À l’inverse, plus la fréquence d’une harmonique est élevée, plus sa période est courte et plus elle est susceptible de provoquer de rapides changements dans l’évolution de la forme d’onde globale.
Or la forme d’onde en dent de scie comporte une discontinuité, le phénomène le moins doux qui puisse se présenter. Ainsi, on peut admettre qu’un maximum d’harmoniques soient nécessaires pour générer cette discontinuité.
Utilisation musicale de la dent de scie
Cette description de la formation d’un son de violon est extrêmement schématique, car un violon est un instrument très complexe. Cependant, on constate dans l’exemple audio suivant que cette analogie peut être acceptable. En effet voici le son obtenupar une dent de scie, sans autre artifice.
Ce qui n’est certes pas très probant en soi ! Mais si on travaille cette onde dans d’autres modules offerts par la synthèse, on arrive à restituer assez correctement un ensemble de violons (ouverture de Rienzi, Wagner).
Mais avant d’aborder ces autres modules de synthèse, restons encore un moment sur la forme d’onde.
Travail approfondi de la forme d’onde
À l’écoute de la dent de scie, il est clair que ce son est trop agressif. Il suffit dès lors de filtrer les harmoniques comme représenté sur cette figure, à droite :
Observez que le profil spectral ressemble toujours à celui de la dent-de-scie, mais que les amplitudes des harmoniques ont subi quelques modifications. Les phases également ont été modifiées. En revanche, la forme d’onde n’a plus grand-chose en commun avec une dent de scie. Les phénomènes physiques liés à un instrument à cordes rendent la modélisation bien plus complexe que la première approche qui a été proposée au début de ce chapitre. Ainsi, si à notre niveau de découverte, une modélisation approximative est intéressante pour éclairer les mécanismes en jeu, il faut garder à l’esprit la complexité du monde réel. Voici le résultat audio de cette forme d’onde, jouée sur une note grave pour rappeler le violoncelle, et qui s’approche de l’instrument réel. Rappelons qu’il s’agit de l’onde brute, sans aucune autre manipulation.
Lorsqu’intervient le talent
Avec beaucoup de talent, on peut tirer de véritables orchestres de ces formes d’ondes comme dans cet exemple où Tomita interprète une Pavane de Maurice Ravel avec comme seul outil un synthétiseur.
L’imitation d’instruments réels est certes une voie à explorer, mais la synthèse ouvre des horizons imaginaires telle cette séquence élaborée par Klaus Schulze et reproduite ici par un logiciel.
L’échantillonnage
Une forme d’onde complexe peut également être obtenue par enregistrement d’un échantillon d’un son naturel : c’est l’échantillonnage (ou sampling). Des techniques particulières sont alors mises en oeuvre pour rendre ces échantillons intéressants pour un usage musical.
Ainsi se termine cet article sur l’onde sonore et ses applications dans le domaine de la synthèse. Pour comprendre l’ensemble des modules qui participent à la création d’un timbre de synthèse dans son ensemble, il faut maintenant s’intéresser aux filtres, aux oscillateurs basse fréquence (LFO), aux enveloppes, etc.