L'échantillonnage - La synthèse sonore - 17e partie

Quelle est donc cette super­che­rie ? Comme nous l’avons vu dans le précé­dent article, il faut tout d’abord consi­dé­rer que cette voie a été choi­sie par certains en réponse à la complexité trop impor­tante engen­drée par la synthèse addi­tive, et qu’en tant que telle la lecture d’échan­tillons peut donc être perçue comme une évolu­tion natu­relle dans la recherche de nouvelles formes de créa­tion sonore. Ensuite, il faut souli­gner que la lecture d’échan­tillons ne repré­sente que la base de la produc­tion sonore : le son échan­tillonné peut ensuite être, lui aussi, comme une onde produite par un oscil­la­teur, soumis aux autres éléments de la synthèse sonore que sont les filtres, les enve­loppes, les LFOs, etc. Enfin, la lecture d’échan­tillons a tota­le­ment révo­lu­tionné la manière de faire de la musique de ces dernières décen­nies, que ce soit à travers la lecture de tables d’ondes sur les synthé­ti­seurs ou bien l’ap­pa­ri­tion des « samplers » (échan­tillon­neurs) maté­riels ou virtuels.

Mais voyons d’abord ce qu’est exac­te­ment l’échan­tillon­nage, quitte à nous éloi­gner momen­ta­né­ment de la synthèse à propre­ment parler…

Échan­tillon­nage

L’échan­tillon­nage est le fait d’en­re­gis­trer de manière numé­rique un signal analo­gique, via un conver­tis­seur analo­gique-numé­rique (CAN – Analo­gic Digi­tal Conver­ter, ADC, en anglais). Mais pourquoi appe­ler cela de l’échan­tillon­nage ? Simple­ment parce que, contrai­re­ment à un enre­gis­tre­ment analo­gique (magné­tique sur bande, par exemple) qui va enre­gis­trer le signal en continu, l’en­re­gis­tre­ment numé­rique ne va préle­ver que des échan­tillons de signal, à inter­valles régu­liers.

Ainsi, la norme pour un enre­gis­tre­ment numé­rique sur CD est un taux d’échan­tillon­nage à 44,1 kHz, codé sur 16 bits. Ce qui signi­fie que le système va « copier » 44 100 échan­tillons par seconde du signal origi­nal, et que chacun de ces échan­tillons sera codé par un nombre binaire à 16 posi­tions. Un filtre de lissage est ensuite employé pour homo­gé­néi­ser la repro­duc­tion sonore d’un échan­tillon à l’autre.

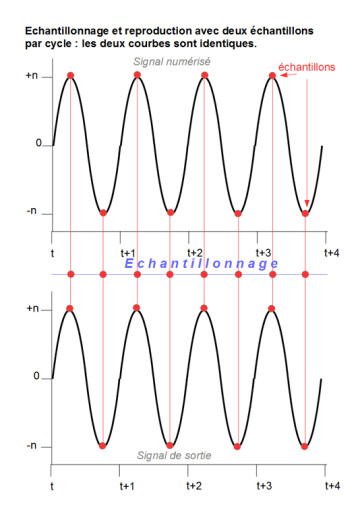
Ce nombre, 44,1 kHz, a été choisi pour la raison suivante. Il a été démon­tré qu’il faut au moins deux échan­tillons par cycle d’une forme d’onde donnée (voir articles 2 et 3 de cette série concer­nant les ondes et leurs cycles) pour que celle-ci soit repro­duite correc­te­ment par le système de lecture et le conver­tis­seur numé­rique-analo­gique (CNA – Digi­tal Analog Conver­ter, DAC, en anglais).

Or, comme la limite supé­rieure de l’au­di­tion humaine est théo­rique­ment de 20 kHz, il faut donc un taux d’échan­tillon­nage d’au moins 40 kHz. Et comme certaines personnes entendent au-delà de cette limite – Rudolph Kœnig, ingé­nieur à l’ori­gine des normes inter­na­tio­nales d’acous­tique, enten­dait jusqu’à 23 kHz – il a été décidé de permettre la repro­duc­tion jusqu’à 22 kHz. 

Toute­fois, ce n’est pas la seule raison. 

Fréquence de Nyquist et repli

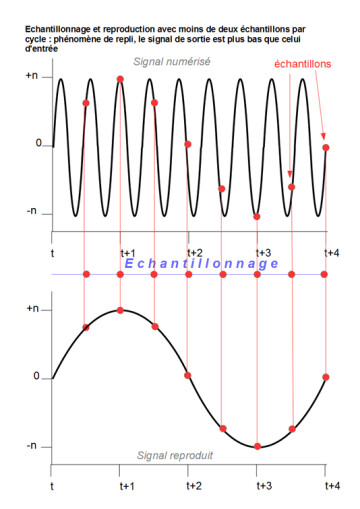
La fréquence égale à la moitié du taux maxi­mal d’échan­tillon­nage d’un système est appe­lée fréquence de Nyquist. Et les sons qui dépassent cette fréquence lors d’un enre­gis­tre­ment numé­rique sont repro­duits lors de la lecture dans le domaine des basses fréquences. Ils viennent ainsi « para­si­ter » le signal. On appelle cela le phéno­mène de « repli de fréquences ». Et là, il s’avère que les 44,1 kHz de la norme CD peuvent ne pas être encore suffi­sants.

Exemple : le troi­sième harmo­nique d’un son à 12,5 kHz est égal à 37,5 kHz, donc a priori inau­dible pour l’être humain. Sauf qu’avec un système à 44,1 kHz, et par le phéno­mène de repli, il se trouve trans­formé en un signal à (44,1 – 37,5) = 6,6 kHz, parfai­te­ment audi­ble… et gênant. Il faudrait un système fonc­tion­nant à (37,5 × 2) = 75 kHz pour que cette fréquence ne se replie pas dans le domaine audible.

C’est pourquoi on utilise lors de l’en­re­gis­tre­ment un filtre anti-replie­ment pour élimi­ner les fréquences supé­rieures à la fréquence de Nyquist.

Dans certains cas, on peut aussi n’em­ployer en synthèse sonore que des sinu­soïdes à partir de 11,025 kHz, afin de ne produire aucune harmo­nique qui risque­rait de se replier. 

Quoi qu’il en soit, dans le prochain article, nous nous penche­rons plus en détail sur la lecture d’échan­tillons elle-même et ses champs d’ap­pli­ca­tion.