Depuis nos premiers cours d’arithmétique, nous avons appris à associer les notions de quantités aux quatre opérations de base : l’addition, la soustraction, la multiplication et la division. Notre esprit a très vite compris que deux bonbons multipliés par deux faisaient bien quatre petites sucreries dans notre poche. Et bien, sur notre belle planète, tout ne fonctionne pas aussi simplement! Avez-vous tout simplement remarqué le matin au petit-déjeuner que lorsque vous ajoutez du lait (à environ 70°C) dans votre thé (lui aussi à 70°C), cela ne faisait pas une boisson à 140°C ! Donc toutes les variables n’obéissent pas uniquement aux lois des quatre opérations de base. C’est le cas des intensités sonores qui ne s’ajoutent pas et ne se multiplient pas comme les bonbons, mais se combinent suivant une autre loi, celle des logarithmes décimaux.
Depuis nos premiers cours d’arithmétique, nous avons appris à associer les notions de quantités aux quatre opérations de base : l’addition, la soustraction, la multiplication et la division. Notre esprit a très vite compris que deux bonbons multipliés par deux faisaient bien quatre petites sucreries dans notre poche. Et bien, sur notre belle planète, tout ne fonctionne pas aussi simplement! Avez-vous tout simplement remarqué le matin au petit-déjeuner que lorsque vous ajoutez du lait (à environ 70°C) dans votre thé (lui aussi à 70°C), cela ne faisait pas une boisson à 140°C ! Donc toutes les variables n’obéissent pas uniquement aux lois des quatre opérations de base. C’est le cas des intensités sonores qui ne s’ajoutent pas et ne se multiplient pas comme les bonbons, mais se combinent suivant une autre loi, celle des logarithmes décimaux.
Je n’entends rien, parlez deux fois plus fort
Eh bien, vous n’entendrez pas deux fois mieux! Pour tous les sens humains, la sensation est proportionnelle au logarithme de l’excitation, c’est la loi de Fechner. Pour avoir la sensation que le volume sonore ait doublé, il faut en réalité multiplier la puissance de la source par 10.
Cette sensation est subjective, elle permettra de définir une unité de mesure tenant compte des différences donc une unité de comparaison appelée le Bel, égal à 10 décibels.
Log 10 P/ P= Log 10 = 1 Bel = 10 dB
(Nous rappelons que le Log à base 10 de 10 est égal à 1)
Pour calculer en dB, la variation d’intensité x entre deux sources de pression acoustique P1 et P2, xdB= 10 Log P1 /P2
Plus on est de fous, plus on fait de bruit!
Exact, mais encore une fois pas dans les proportions que l’on pourrait imaginer au point de départ. Le tableau suivant vous aidera à comprendre comment double la sensation de volume sonore chaque fois que l’on multiplie la puissance de la source sonore par 10.
|
Sensation de volume sonore
|
1
|
2
|
4
|
8
|
16
|
|
Variation en Bel
|
0
|
1
|
2
|
3
|
4
|
Et quand on parle en même temps tous les deux à la même puissance ?
Déjà, on ne risque pas de se comprendre… habitués des scènes de ménage, réfléchissez! Quoi qu’il en soit, l’intensité en dB ne doublera pas, ce qui réconfortera les enseignants aux classes dissipées, deux élèves qui parlent en même temps ne font pas deux fois plus de bruit dans la classe ! Il y aura cependant une augmentation du volume sonore global.
La variation de ce volume sonore exprimée en dB se calcule de la manière suivante :
Log 2P/P = Log 2= 0,3 Bel= 3 dB (nous rappelons que Log décimal de 2 est égal à 0,3)
Donc lorsque deux élèves parlent en même temps à pression acoustique égale, le niveau sonore de la classe n’a augmenté que de 3 décibels! Donc, amis enseignants, laissez-les s’exprimer!
De l’unité de comparaison à l’unité de valeur
Pour passer de l’unité de comparaison à l’unité de valeur, il faut définir un point de départ comme le 0°C de la température par exemple.
Pour l’intensité sonore, nous prendrons pour référence, la valeur de la pression P0 correspondant à la limite de perception de notre oreille pour la fréquence de 1000 Hertz.
Cette valeur P0 est égale à 2. 10–5 Pascals. (Pa)
Ce nouveau dB s’appellera le dB SPL (Sound Pressure Level, niveau de pression sonore, sous-entendu « limite nécessaire » à l’audition.)
Nous savons que la puissance de l’onde sonore varie avec le carré de la pression donc:
10 Log (P/P0)2 = 20 Log ( P / P0) = 20 Log (P/ 2. 10–5) = 0 dB SPL
La pression est exprimée en Pascal. Nous rappelons pour les allergiques aux maths que Log xY= y Log x
Quelques exemples chiffrés
Un séchoir à cheveux peut atteindre une intensité allant de 60 à 95 dB, une rame de métro, de 90 à 115 dB, un concert symphonique 110 dB, un concert de rock 110 à 120 dB (comme quoi ce n’est pas forcément le style de musique choisie qui est responsable systématiquement des risques de nuisances auditives!), un incendie peut atteindre 150 dB!
Et nos oreilles dans tout cela ?
Si nous nous reportons au diagramme de Fletcher, nous constatons que le seuil de douleur se situe autour de 120 et 130 dB. Et heureusement que les intensités ne s’ajoutent pas, car imaginez ce que donnerait un embouteillage s’il fallait multiplier l’intensité moyenne d’un moteur par le nombre de véhicules, on serait bien au-delà des 120 dB!
En concert, la valeur légale autorisée est de 105 dB SPL… À méditer ! (voir encadré page 6)
Nos oreilles sont fragiles même si elles n’expriment pas leurs souffrances dans l’immédiat. Ménageons-les et apprenons à mieux évaluer les nuisances qui pourraient les détériorer. Un prochain dossier sera consacré à l’audition ou comment mieux se connaître pour mieux se protéger.
-
Bruits légers, entre 0 et 30 dB
-
Bruits gênants, entre 30 et 60 dB
-
Bruits fatigants, entre 60 et 100 dB
-
Bruits dangereux, au-delà de 100 dB
Le site du CIDB renseigne de manière détaillée sur les nuisances sonores, vous pourrez y trouver des chiffres intéressants dont il est important de prendre conscience.
Nous allons compléter ce premier volet théorique par une seconde partie, consacrée cette fois à un usage plus technique des machines, nous allons aborder l’ajustement des paramètres de dynamique au moyen du compresseur et de l’expanseur.
Discret, mais efficace…
Le compresseur n’est en général pas aussi bien connu dans son utilisation comme peut l’être celle de la réverbération ou de l’égaliseur, bien plus spectaculaires au niveau du rendu immédiat. Pourtant, son exploitation peut très vite s’avérer fondamentale lorsque l’on est amené à traiter des voix ou différents instruments à forte dynamique. Comme nous l’avons vu plus haut, les rapports de dynamique peuvent devenir considérables en fonction du nombre de sources mises en œuvre ou de leur nature. Si l’oreille s’accommode assez bien d’importantes sautes de pression acoustique, nos équipements électriques sont parfois plus chatouilleux et l’utilisation du compresseur résoudra pas mal de problèmes liés à la dynamique de sources parfois difficilement contrôlables…
Plus fort, moins fort…
Comme son nom l’indique, le compresseur aura comme fonction de tasser la dynamique d’un signal afin de permettre sa transmission sans détériorations. Pas très différent du réglage de gain d’entrée d’une tranche de console ou de son fader, direz-vous… Eh bien si, car si l’ajustement du gain permet en effet d’adapter le niveau électrique d’une source à celui d’une entrée de console, il n’agit pas sur les fluctuations d’intensité liées au jeu du musicien. Il faudrait à cet effet que le technicien du son puisse instantanément et en continu, ajuster le niveau du fader de la tranche (fig.1). Le compresseur permettra d’ajuster automatiquement le niveau de dynamique d’un signal selon un réglage donné, en fonction d’un seuil de référence donné. Le principe de fonctionnement du compresseur est donné par son hypsogramme.
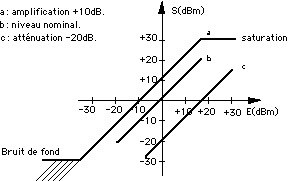 |
Figure 1 : un hypsogramme de réglage d’un fader
Le diagramme met en évidence le lien entre niveaux d’entrée et de sortie. On peut constater la proportionnalité des ajustements de niveaux. Dans le cas d’un compresseur, on va définir un seuil à partir duquel le gain de sortie ne sera plus linéaire, mais atténué. Les deux exemples d’hypsogrammes ci-dessous mettent en évidence le point d’inflexion de la droite, correspondant au point à partir duquel le niveau de sortie ne sera plus linéaire. On nomme ce point « seuil » ou « threshold ». La déviation à partir du seuil met en évidence une progression du niveau de sortie plus lente qu’en dessous: on est donc en train de compresser le signal. On exprime cette compression comme un rapport du type 4 :1 ou 2 :1, comme dans nos exemples (Fig.2). Cela signifie qu’un gain d’entrée de 4 correspondra à un gain en sortie de 1 dans le premier cas, et dans le second, qu’un gain de 2 en entrée ne sera que de 1 en sortie. Une belle application supplémentaire de ce qu’est une progression logarithmique… Enfin, on peut remarquer que notre droite de transfert ne passe pas forcément par le 0 des deux axes ; on définit alors un « gain sous le seuil » qui va permettre d’augmenter le niveau global du signal avant qu’il soit compressé. Cela revient alors à réduire la dynamique globale de la source, puisque les faibles niveaux seront rehaussés et les forts, compressés… Un type de son qu’affectionnent certaines stations de radio.

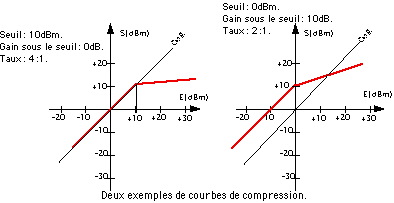 |
Figure 2 : on repère aisément le point d’inflexion de la droite (le niveau du seuil) et la progression du niveau de sortie qui correspond au taux de compression.
Dans un sens ou dans l’autre…
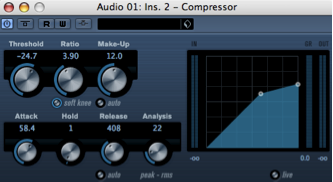
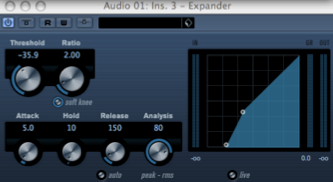
Dans certains cas, il peut être judicieux de monter plus que normalement le niveau d’un signal et ce, jusqu’à un seuil défini. C’est le rôle de l’expanseur que l’on peut considérer comme… un compresseur à l’envers! Si l’on compare les plug-ins de compresseur et d’expanseur de Cubase, on note une évidente similitude, hormis le fait donc, que les pentes d’action sont inversées.
 |
|
 |
On en met où ?
Comme nous l’avons dit plus haut, le compresseur trouvera pleinement son utilité pour toutes les sources à forte dynamique. Son placement sera dans la chaîne d’insert, entre la source et la sortie de tranche de la console. Son utilisation aura forcément une incidence sur les transitoires d’attaque de l’instrument : si le taux appliqué est très important, un effet de pompage peut déformer considérablement un son. Il importe donc de mesurer l’incidence des réglages de manière à ce que le résultat conserve une bonne crédibilité après traitement… Dans le cas d’une voix chantée ou parlée, le compresseur permettra d’atténuer les effets de consonnes un peu violentes. Pour une grosse caisse, une caisse claire, les cuivres ou encore dans certains cas le piano, il pourra avantageusement simplifier la vie du technicien du son. À noter aussi, l’utilisation un peu particulière sur la guitare : en choisissant un seuil assez bas et un taux de compression élevé, on obtient un effet de sustain qui gomme les attaques et dont Santana, entre autres, fit un usage intensif… Sur la diffusion finale ou sur le mix, il pourra être utile de compresser, comme nous l’avons évoqué plus haut, afin de réduire la plage de dynamique globale: cela peut être plus confortable pour l’auditeur, même si l’identité du son des instruments dans le mixage peut en prendre un sacré coup! À l’extrême, un taux de compression infini (∞:1, ce qui signifie qu’une fois le seuil atteint, le niveau atteint sera constant…) transformera notre compresseur en limiteur. Bien pratique dans certains cas pour calmer les ardeurs incontrôlables des amateurs de nuisances sonores, ou réglementaire pour respecter la loi des 105dB ! (voir encadré) Enfin, pour terminer, on utilise en mastering un appareil nommé compresseur multi-bandes qui permettra un ajustement dynamique par zones de fréquences, mais c’est une autre histoire…
