Fréquence d'échantillonnage - Les secrets de l'audionumérique

Le jargon numé­rique peut rapi­de­ment dérou­ter le musi­cien. Fréquence d’échan­tillon­nage, quan­ti­fi­ca­tion… Toutes ces notions cachent des aspects élémen­taires de l’au­dio­nu­mé­rique.

Ce dossier étant rela­ti­ve­ment pointu, il est forte­ment conseillé de lire préa­la­ble­ment le dossier d’in­tro­duc­tion au monde numé­rique si vous êtes débu­tant.

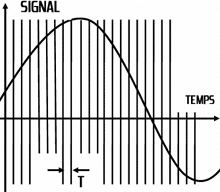
Un signal audio sous forme analo­gique est une forme d’onde élec­trique conti­nue dans le temps. La tâche d’un conver­tis­seur analo­gique-numé­rique est de traduire ce signal en une séquence de nombres binaires. La méthode d’échan­tillon­nage employée dans un conver­tis­seur analo­gique/numé­rique consiste à mesu­rer, ou encore « quan­ti­fier », l’am­pli­tude de la forme d’onde à des inter­valles de temps régu­liers :

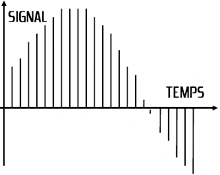
Ici, un signal quel­conque est échan­tillonné à inter­valles de temps régu­liers t (à gauche) afin de géné­rer de courtes impul­sions (à droite) dont les ampli­tudes repré­sentent l’am­pli­tude instan­ta­née du signal

Sur ce diagramme, il appa­raît clai­re­ment que les impul­sions repré­sentent les ampli­tudes instan­ta­nées du signal à chaque instant t. La période T est appe­lée période d’échan­tillon­nage. Les échan­tillons peuvent être consi­dé­rés comme des images instan­ta­nées du signal audio qui, assem­blées dans une séquence, donnent une repré­sen­ta­tion de la forme d’onde conti­nue, de la même manière que la séquence d’images d’un film, proje­tée en succes­sion rapide, donne l’illu­sion d’une image en mouve­ment continu.

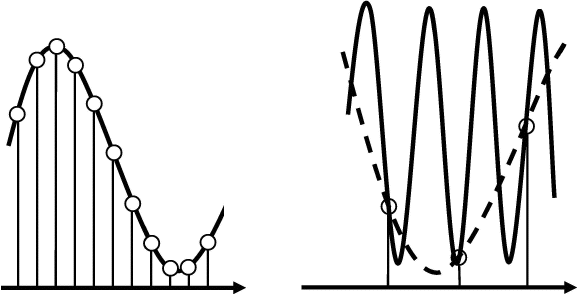
Afin de repré­sen­ter les détails fins du signal, il est néces­saire de préle­ver un grand nombre de ces échan­tillons à chaque seconde. Comme on peut le voir dans la figure suivante, si on prélève trop peu d’échan­tillons par cycle, ils peuvent alors être inter­pré­tés comme la repré­sen­ta­tion d’une forme d’onde diffé­rente de la forme d’onde d’ori­gine échan­tillon­née. Ce problème est en fait un exemple de phéno­mène connu sous le nom de replie­ment de spectre (ou alia­sing). Un alias est un produit indé­si­rable du signal d’ori­gine surve­nant lors de sa recons­truc­tion en conver­sion numé­rique/analo­gique.

Le signal en entrée est une sinu­soïde :  A gauche on prélève de nombreux échan­tillons par cycle de l’onde.  A droite on prélève moins de deux échan­tillons par cycle. Il est alors impos­sible de recons­truire une forme d’onde de fréquence plus haute à partir des échan­tillons, c’est un exemple de replie­ment du spectre (alia­sing).

Il nous faut donc trou­ver la bonne période d’échan­tillon­nage, c’est à dire une période qui permette de resti­tuer assez fidè­le­ment le signal d’ori­gine. On pour­rait être tenté de dimi­nuer le plus possible cette période mais on se confron­te­rait alors à des problèmes de stockage ou de bande passante. En effet, prendre plus d’échan­tillons que néces­saire va impliquer plus d’in­for­ma­tions et donc un besoin accru de ressources. Les mathé­ma­tiques nous indiquent que, pour obte­nir les infor­ma­tions néces­saires à la carac­té­ri­sa­tion du signal, il faut préle­ver au moins deux échan­tillons par cycle audio, c’est à dire avoir une fréquence d’échan­tillon­nage deux fois supé­rieure à la fréquence maxi­male du signal. Afin de justi­fier ce résul­tat, nous pouvons consi­dé­rer le proces­sus d’échan­tillon­nage en termes de modu­la­tion :

Aspect modu­la­tion

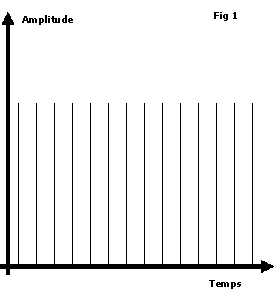
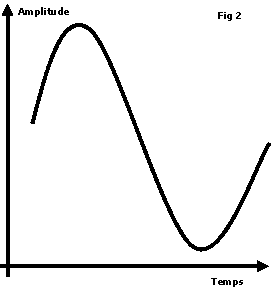
La forme d’onde conti­nue (signal sonore d’ori­gine) que l’on souhaite échan­tillon­ner est utili­sée pour modu­ler une chaîne régu­lière d’im­pul­sions (figure 2 suivante). La fréquence de ces impul­sions est appe­lée fréquence d’échan­tillon­nage. Avant modu­la­tion, toutes les impul­sions ont la même ampli­tude. Après modu­la­tion, l’am­pli­tude des impul­sions est modi­fiée en fonc­tion de l’am­pli­tude instan­ta­née du signal audio. Ce procédé est appelé modu­la­tion d’im­pul­sions en ampli­tude.

Résul­tat de la modu­la­tion des deux signaux précé­dents : 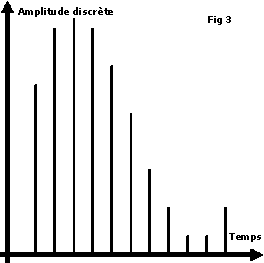En modu­la­tion d’im­pul­sions par ampli­tude, l’am­pli­tude instan­ta­née des impul­sions (à droite) est modu­lée par l’am­pli­tude instan­ta­née du signal audio (à gauche)

Aspect spec­tral

Nota Bene : dans tout ce chapitre, on notera Fs la fréquence d’échan­tillon­nage du signal.

Pour­sui­vons en consi­dé­rant le domaine fréquen­tiel (ou spec­tral) pour bien comprendre ce qu’est l’échan­tillon­nage.

Tout signal est décom­po­sable en une somme de sinu­soïdes de fréquences diffé­rentes. Par exemple un extrait musi­cal est usuel­le­ment composé de fréquences basses, médium et aiguës. Ces grou­pe­ments repré­sentent en fait des familles de fréquences proches. Mais il suffit de conti­nuer le raison­ne­ment en décou­per toujours plus les bandes de fréquences en bandes plus petites jusqu’à consi­dé­rer toutes les fréquences sépa­ré­ment. Parler du spectre d’un signal sonore c’est décrire la puis­sance (acous­tique, élec­trique…) de celui-ci pour chaque bande « infi­ni­ment petite » de fréquence. Voir la défi­ni­tion du spectre sonore pour plus d’in­for­ma­tions.

Le spectre de fréquences du signal modulé est montré sur la figure suivante. On remarque qu’en plus du spectre d’ori­gine avant échan­tillon­nage, appa­raît main­te­nant un certain nombre de spectres addi­tion­nels, chacun étant centré sur des multiples de la fréquence d’échan­tillon­nage. Des bandes secon­daires résul­tant de la modu­la­tion d’am­pli­tude ont été produites de chaque côté de la fréquence d’échan­tillon­nage et de ses multiples. Celles-ci s’étendent en dessous et au-dessus de la fréquence d’échan­tillon­nage et de ses multiples sur des largeurs équi­va­lentes à celle de la bande de base. En d’autres termes, ces bandes secon­daires sont des paires d’images miroir de la bande audio.

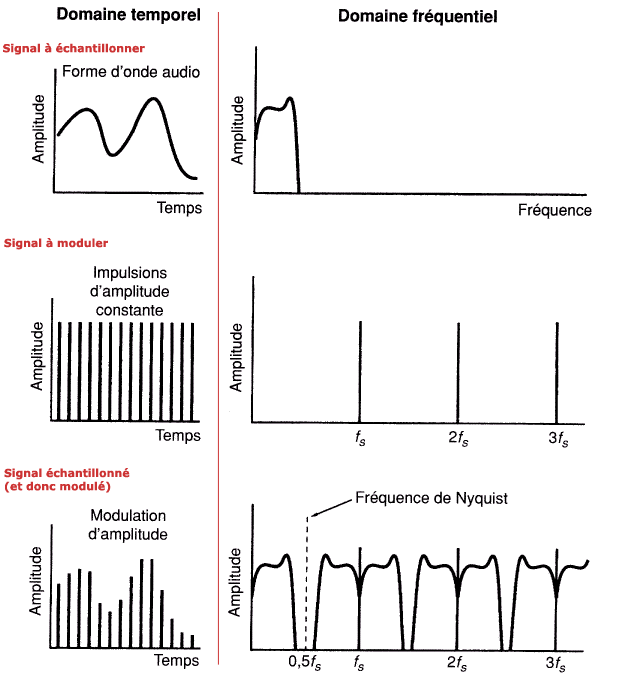
Ce sont ces spectres addi­tion­nels de part et d’autre de la fréquence d’échan­tillon­nage qui vont impo­ser d’échan­tillon­ner à une fréquence au moins double de la plus haute fréquence présente dans le signal. Il suffit d’ima­gi­ner que la fréquence d’échan­tillon­nage ne soit pas suffi­sam­ment grande. Le spectre origi­nal et le spectre image vont entrer en colli­sion créant des alias (zone bleue ci dessous), c’est à dire ajou­tant des sons initia­le­ment absents.

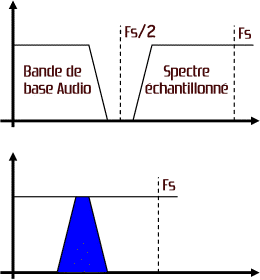
En étudiant la figure précé­dente, on comprend pourquoi la fréquence d’échan­tillon­nage doit être supé­rieure au double de la fréquence audio la plus élevée du signal. On note qu’une exten­sion de la bande de base au-dessus de la fréquence de Nyquist (moitié de la fréquence d’échan­tillon­nage Fs) produit un recou­vre­ment de la bande secon­daire infé­rieure de la première répé­ti­tion spec­trale par la limite supé­rieure de la bande de base. Conjoin­te­ment, une dimi­nu­tion de la fréquence d’échan­tillon­nage a les mêmes consé­quences. Dans le premier exemple, la hauteur tonale de la bande de base reste suffi­sam­ment basse pour que les bandes secon­daires échan­tillon­nées restent au-dessus du spectre audio ; dans le second, une fréquence d’échan­tillon­nage trop faible entraîne une colli­sion des spectres, géné­rant ainsi des recou­vre­ment du spectre origi­nal dans la bande de base, autre­ment dit des distor­sions (défor­ma­tions du signal en fonc­tion de lui même).

Vous êtes perdu ? Prenons un exemple plus simple. Dans la mesure où l’image ciné­ma­to­gra­phique consti­tue égale­ment un exemple de signal échan­tillonné, l’ef­fet ciné­ma­to­gra­phique bien connu de « la roue qui tourne à l’en­vers » rend le phéno­mène de replie­ment du spectre (ou alia­sing) visible et donc plus concret. Pour le film, les images sont en prin­cipe mises à un taux de 24 par seconde. Si une roue marquée est filmée, elle semblera tour­ner dans le sens de la marche tant que sa vitesse de rota­tion reste infé­rieure au nombre d’images par secondes filmé par la caméra. Si la vitesse de rota­tion augmente, la roue semblera ralen­tir, s’ar­rê­ter, puis se mettre à tour­ner en sens inverse, et cette impres­sion de mouve­ment rétro­grade augmen­tera si la vitesse de rota­tion de la roue augmente encore. Ce mouve­ment rétro­grade est en fait l’alias généré par un échan­tillon­nage trop faible. En audio­nu­mé­rique, si le phéno­mène de replie­ment de spectre n’est pas contrôlé, on aperçoit audi­ti­ve­ment l’équi­valent du mouve­ment rétro­grade d’une roue filmée sous la forme de compo­santes sonores (origi­nel­le­ment absentes) dans le spectre audible. Leur fréquence décroît à mesure que la fréquence du signal d’ori­gine augmente. Avec des conver­tis­seurs basiques, il est donc néces­saire de filtrer le signal audio avant échan­tillon­nage afin de suppri­mer toute compo­sante dont la fréquence excède la fréquence de Nyquist (la moitié de la fréquence d’échan­tillon­nage).

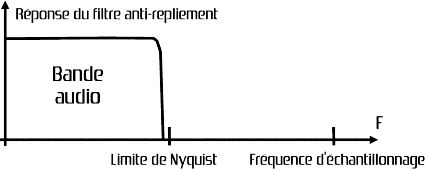
En réalité, comme les filtres ne sont pas parfaits, on choi­sit une fréquence d’échan­tillon­nage légè­re­ment supé­rieure au double de la fréquence audio la plus élevée devant être repré­sen­tée. On peut ainsi accep­ter des filtres qui coupent de façon un peu plus douce. Les filtres inté­grés aux conver­tis­seurs analo­gique/numé­rique ([def]CAN[/def]) et numé­rique/analo­gique ([def]CNA[/def]) ont un effet prononcé sur la qualité sonore, puisqu’ils déter­minent la linéa­rité de la réponse en fréquence dans la bande audio ainsi que la linéa­rité du système. Dans un conver­tis­seur clas­sique de bonne qualité, le filtre doit reje­ter tous les signaux au-dessus de la moitié de la fréquence d’échan­tillon­nage (fréquence de Nyquist) avec une atté­nua­tion d’au moins 80dB.

Le procédé de suréchan­tillon­nage (que nous verrons dans un autre dossier), qui échan­tillonne à des fréquences plus élevées, a contri­bué à atté­nuer les problèmes du filtrage analo­gique dans la mesure où la première répé­ti­tion de la bande de base est reje­tée à une fréquence beau­coup plus élevée, permet­tant ainsi l’em­ploi d’un filtre de pente moins raide.

La quan­ti­fi­ca­tion

Après l’échan­tillon­nage, la chaîne d’im­pul­sions modu­lées est quan­ti­fiée. Quan­ti­fier un signal échan­tillonné consiste à placer les ampli­tudes des échan­tillons sur une échelle de valeurs à inter­valles fixes (voir figure suivante).

Signal avant quan­ti­fi­ca­tion :


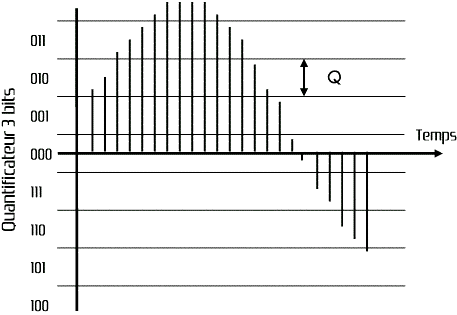
Signal après quan­ti­fi­ca­tion :

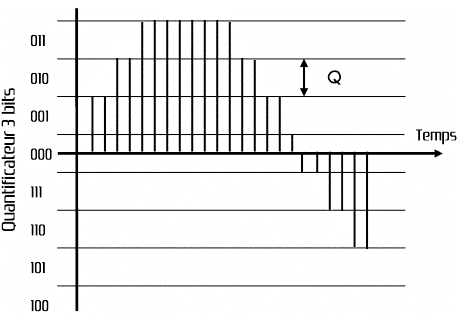
Le quan­ti­fi­ca­teur déter­mine dans quel inter­valle de quan­ti­fi­ca­tion (de taille Q) l’échan­tillon se situe, et lui affecte une valeur qui repré­sente le point central de cet inter­valle. Ce procédé permet d’at­tri­buer à l’am­pli­tude de chaque échan­tillon un mot binaire unique. En quan­ti­fi­ca­tion linéaire, chaque pas de quan­ti­fi­ca­tion repré­sente une incré­men­ta­tion iden­tique de la tension du signal. De plus, dans le système binaire le nombre de pas de quan­ti­fi­ca­tion est égal à 2 puis­sance n, où n est le nombre de bits des mots binaires utili­sés pour repré­sen­ter chaque échan­tillon. En consé­quence, un quan­ti­fi­ca­teur 4 bits offre seule­ment 2 puis­sance 4 (16) niveaux de quan­ti­fi­ca­tion, alors qu’un quan­ti­fi­ca­teur 16 bits en offre 2 puis­sance 16 soit 65 536.

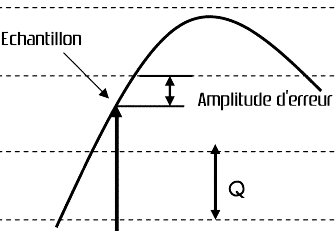
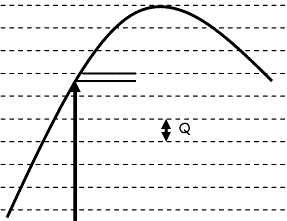
Il appa­raît clai­re­ment qu’une erreur inter­vient dans la quan­ti­fi­ca­tion, puisqu’on dispose d’un nombre limité de niveaux diffé­rents pour repré­sen­ter l’am­pli­tude du signal à chaque instant. La valeur maxi­male de l’er­reur est de 0.5 Q. En consé­quence, plus le nombre de bits par échan­tillon est impor­tant, et plus l’er­reur est petite (voir figure suivante).

L’er­reur maxi­male de quan­ti­fi­ca­tion est égale à la moitié de l’in­ter­valle de quan­ti­fi­ca­tion (Q). A gauche le nombre d’in­ter­valles est faible et l’er­reur est impor­tante alors qu’à droite le nombre d’in­ter­valles est plus grand et l’er­reur devient plus petite.

L’er­reur de quan­ti­fi­ca­tion peut être consi­dé­rée comme un signal indé­si­rable ajouté au signal utile (voir figure suivante). Les signaux indé­si­rables sont clas­si­fiés comme distor­sion ou bruit en fonc­tion de leurs carac­té­ris­tiques. La nature du signal d’er­reur de quan­ti­fi­ca­tion dépend du niveau et de la nature du signal audio qui lui est ratta­ché.

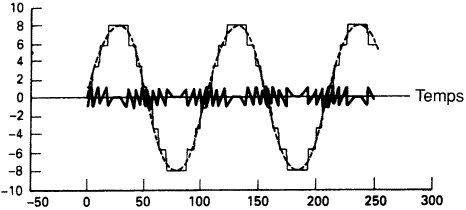L’er­reur de quan­ti­fi­ca­tion vue comme signal indé­si­rable ajouté aux valeurs d’échan­tillons d’ori­gine. Ici, l’er­reur est direc­te­ment corré­lée au signal et appa­raî­tra comme de la distor­sion.

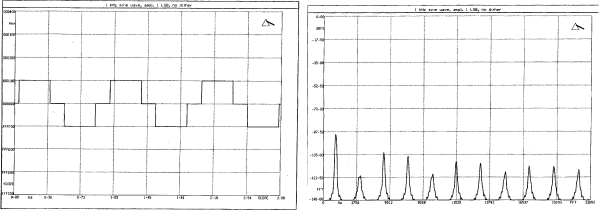
Pour plus de clarté, consi­dé­rons l’exemple d’une quan­ti­fi­ca­tion 16 bits d’un signal sinu­soï­dal, échan­tillonné, de très bas niveau. Son niveau est tout juste suffi­sant pour affec­ter la valeur du bit le moins signi­fi­ca­tif à son niveau maxi­mal (voir figure suivante à gauche). Un tel signal aura une erreur de quan­ti­fi­ca­tion pério­dique et forte­ment corré­lée au signal, appor­tant de la distor­sion harmo­nique.

La figure de droite montre le spectre d’un signal de ce type analysé dans le domaine numé­rique. La distor­sion engen­drée appa­raît clai­re­ment (avec une prédo­mi­nance des harmo­niques impaires) en addi­tion de la fonda­men­tale d’ori­gine corres­pon­dant à la sonu­soïde. Une fois le signal descendu au-dessous du niveau auquel l’élé­ment binaire de poids faible (LSB) se déclenche, il n’y a plu aucune modu­la­tion. Du point de vue audible, on constate alors la dispa­ri­tion soudaine d’un signal très forte­ment distordu. Un signal sinu­soï­dal de plus haut niveau traver­se­rait un plus grand nombre d’in­ter­valles de quan­ti­fi­ca­tion et géné­rait une plus grande quan­tité de valeurs d’échan­tillon non nulles. Quand le niveau du signal augmente, l’er­reur de quan­ti­fi­ca­tion (toujours avec une valeur maxi­male de 0.5Q), devient de plus en plus petite compa­rée au niveau total du signal. La corré­la­tion entre l’er­reur et le signal dimi­nue graduel­le­ment.

On consi­dère main­te­nant un signal musi­cal d’un niveau raison­nable. Les carac­té­ris­tiques spec­trales et l’am­pli­tude d’un tel signal varient beau­coup : cela confère à l’er­reur de quan­ti­fi­ca­tion une nature assez aléa­toire. En d’autres termes, l’er­reur de quan­ti­fi­ca­tion ressemble plus à du bruit qu’à de la distor­sion, d’ou le terme de « bruit de quan­ti­fi­ca­tion » couram­ment employé pour en décrire l’ef­fet audible.

L’ana­lyse de la puis­sance de l’er­reur de quan­ti­fi­ca­tion (en assu­mant que sa nature se rapproche du bruit) montre une ampli­tude effi­cace élec­trique de Q sur racine de 12, où Q est l’in­cré­ment de tension repré­senté par un inter­valle de quan­ti­fi­ca­tion. Ainsi, le rapport signal/bruit d’un signal idéal de n bits peut être approxi­ma­ti­ve­ment donné par : (6.02n + 1.76) dB. Ceci implique un rapport signal/bruit théo­rique appro­ché d’un peu plus de 6 dB par bit. Un conver­tis­seur 16 bits doit affi­cher un rapport signal/bruit autour de 98 dB, et un conver­tis­seur 8 bits autour de 50 dB. Par ailleurs, d’autres erreurs sont intro­duites si le signal à échan­tillon­ner présente une ampli­tude supé­rieure à la plage de conver­sion. Les signaux dépas­sants cette limite sont dure­ment écrê­tés ce qui induit une distor­sion très sévère

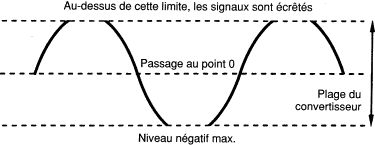Les signaux qui dépassent le niveau de pic sont dure­ment écrê­tés dans un système audio­nu­mé­rique. Il n’existe pas de valeurs dispo­nibles pour repré­sen­ter les échan­tillons.

Limi­ta­tions psycho-acous­tiques & choix tech­niques

La ques­tion de savoir quel taux d’échan­tillon­nage et quelle réso­lu­tion sont requis pour accé­der à une qualité audio donnée trouvent certaines réponses en rela­tion avec les capa­ci­tés de l’oreille humaine, laquelle doit certai­ne­ment être consi­dé­rée comme l’ar­bitre ultime.

L’au­dio­nu­mé­rique permet d’at­teindre les limites de l’oreille humaine en termes de qualité sonore. Cepen­dant, l’au­dio­nu­mé­rique, mal maîtrisé, peut «  sonner  » de façon très médiocre, et le terme numé­rique n’im­plique pas auto­ma­tique­ment une haute qualité sonore. Les choix des para­mètres d’échan­tillon­nage et des méthodes de mise en forme de bruit affectent la réponse en fréquence, la distor­sion et la dyna­mique perçue.

Les capa­ci­tés de l’oreille humaine pour­raient être consi­dé­rées comme le stan­dard en regard duquel la qualité des systèmes numé­riques serait évaluée. On peut en effet défendre l’idée que seuls comptent les distor­sions et les bruits percep­tibles par l’oreille. Il pour­rait, par exemple, sembler perti­nent de conce­voir un conver­tis­seur dont le plan­cher de bruit corres­pon­drait au seuil de sensi­bi­lité de l’oreille. La figure suivante montre une courbe typique du seuil de sensi­bi­lité de l’oreille aux niveaux bas, indiquant le niveau de pres­sion acous­tique (SPL, Sound Pres­sure Level) requis pour qu’un son soit tout juste audible.

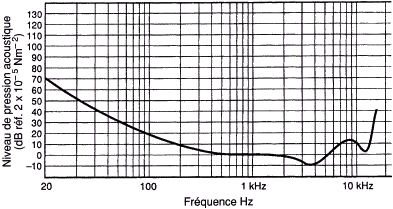
Il faut noter que l’oreille est plus sensible au milieu du spectre audible, autour de 4kHz, et moins sensible dans les zones limites infé­rieure et supé­rieure. Cette courbe est géné­ra­le­ment appe­lée «  champ audible mini­mum  » ou encore «  seuil de l’au­di­tion  ». Elle présente un niveau de pres­sion acous­tique de 0dB (réf. 20 Pa) à 1kHz. Il est toute­fois impor­tant de se rappe­ler que le seuil d’au­di­tion de l’oreille humaine n’est pas une valeur abso­lue mais une valeur statis­tique. Cette notion est capi­tale pour toute recherche qui tente d’éta­blir des critères d’au­di­bi­lité, puisque certains sons, bien que 10 dB infé­rieurs aux seuils admis, conservent une proba­bi­lité de percep­tion qui peut avoi­si­ner la certi­tude. En des termes plus simples : certains ont des oreilles qui enten­dront des niveaux bien plus bas que ceux indiqués sur le graphe précé­dant.

On peut défi­nir la plage dyna­mique comme étant égale à la plage dyna­mique située entre le seuil d’au­di­bi­lité et le plus fort son tolé­rable. Le plus fort son tolé­rable dépend lui aussi de la personne ; toute­fois, on consi­dère géné­ra­le­ment que le seuil de la douleur se situe entre les niveaux de la pres­sion acous­tique de 130 et 140 dB. La plage dyna­mique maxi­male abso­lue de l’oreille humaine se situe donc autour de 140dB à 1kHz, mais bien en deçà aux basses et hautes fréquences. On peut ensuite débattre pour savoir s’il est néces­saire d’en­re­gis­trer et de produire une plage dyna­mique aussi impor­tante. Les travaux menés par Louis Fiel­der et Eliza­beth Cohen ont tenté de défi­nir la plage dyna­mique requise pour les systèmes audio de haute qualité : ils ont exploré les pres­sions extrêmes produites par des sources acous­tiques diverses et les ont compa­rées avec les plan­chers de bruit percep­tible dans des condi­tions acous­tiques réelles.

En s’ap­puyant sur la théo­rie psycho-acous­tique, Fiel­der a pu établir ce qui a une proba­bi­lité d’être entendu à diverses fréquences en termes de bruit et de distor­sion, et a loca­lisé les éléments limi­tant d’une chaîne acous­tique typique. Il a défini la plage dyna­mique comme étant « le rapport entre le niveau de la valeur effi­cace d’un signal (RMS) maxi­mal d’une onde sinu­soï­dale non distor­due produi­sant des pics de niveau égaux à un niveau donné, et le niveau de la valeur effi­cace d’un signal (RMS) d’un bruit blanc limité à 20kHz dont le niveau sonore appa­rent serait le même que le bruit d’une chaîne audio donnée en l’ab­sence de signal  ». Après quoi il a établi que le niveau tout juste audible d’un bruit dont la largeur de bande est de 20kHz est d’un niveau de pres­sion acous­tique d’en­vi­ron 4 dB et que le nombre de pres­ta­tions musi­cales produisent des niveaux de pres­sion acous­tique entre 120 et 129 dB au point d’écoute opti­mal. Il en a déduit que la plage dyna­mique néces­saire à une repro­duc­tion natu­relle était de 122 dB. En prenant en compte les perfor­mances des micro­phones et les limi­ta­tions des enceintes grand public, cette spéci­fi­ca­tion est tombée à 115dB.

Le choix du taux d’échan­tillon­nage déter­mine la largeur maxi­male de bande audio dispo­nible. Un débat sévit concer­nant le choix d’un taux ne dépas­sant pas le strict néces­saire, à savoir le double de la fréquence audio la plus élevée pouvant être repré­sen­tée. D’où le débat secon­daire portant sur la plus haute fréquence audio utile. Par conven­tion, il a été posé que la bande de fréquence audio s’éten­dait jusqu’à 20 kHz, ce qui entraîne des taux tout juste supé­rieurs à 40 kHz. Le choix s’est en fait porté sur deux fréquences d’échan­tillon­nage stan­dard comprises entre 40 et 50 kHz: le taux de 44,1 kHz du disque compact et le taux de 48 kHz dit « profes­sion­nel » bien qu’étant large­ment dépassé aujour­d’hui. Ces fréquences sont enté­ri­nées par le stan­dard AES5 de 1984 (AES est l’abré­via­tion d’Au­dio Engi­nee­ring Society, orga­nisme indé­pen­dant chargé de norma­li­ser l’en­semble des appli­ca­tions audio).

En fait le taux d’échan­tillon­nage de 48 kHz avait été choisi pour offrir une certaine varia­tion des vitesses de défi­le­ment des bandes élec­tro­ma­gné­tiques encore utili­sées au début de l’au­dio­nu­mé­rique pour stocker les données numé­riques; ainsi les risques de replie­ment du spectre étaient amoin­dris du fait de la marge offerte. La fréquence de 44,1 kHz a été établie plus tôt avec le lance­ment du disque compact. Par ailleurs ce taux génère 10 % de données en moins que le taux de 48 kHz, d’où une certaine écono­mie.

On peut d’ailleurs ici s’in­ter­ro­ger sur la prove­nance de cette valeur de 44,1 kHz au combien exotique dans la mesure où l’on cher­chait simple­ment une fréquence supé­rieure au double de la plus haute fréquence audible. La réponse se trouve simple­ment dans le maté­riel dont dispo­saient les cher­cheurs à cette époque. En effet, aux premiers temps de la recherche audio­nu­mé­rique, les débits requis pour le stockage des données, d’en­vi­ron 1 Mbit/seconde, étaient diffi­ciles à atteindre. Les lecteurs de disquette les rendaient possible, mais leurs capa­ci­tés étaient insuf­fi­santes pour des enre­gis­tre­ments d’une certaine durée ; aussi se tourna-t-on vers les enre­gis­treurs vidéo. Ceux-ci furent adap­tés en vue du stockage d’échan­tillons audio, en créant un signal dit pseudo-vidéo qui trans­por­tait des données binaires sous forme de niveau de noir et de blanc. La fréquence d’échan­tillon­nage de tels systèmes fut condi­tion­née par le fait d’être en rela­tion simple avec la struc­ture et la fréquence des trames du stan­dard vidéo utilisé, de façon qu’un nombre entier d’échan­tillons soient enre­gis­trés par ligne utile. Les stan­dards vidéo ont ainsi impo­sés cette fréquence de 44,1 kHz.

Comme on a pu le voir plus haut, le nombre de bits par échan­tillon défini le rapport signal/bruit ainsi que l’éten­due dyna­mique d’un système audio­nu­mé­rique. On ne prend en compte que les systèmes en modu­la­tion par impul­sions codées (PCM) linéaires. Depuis de nombreuses années, la modu­la­tion par impul­sions codées linéaire 16 bits est consi­dé­rée comme la norme pour les appli­ca­tions audio de qualité. C’est en effet le stan­dard du disque compact, capable d’of­frir une dyna­mique satis­fai­sante supé­rieure à 90 dB. Ce stan­dard convient pour la plupart des cas mais ne satis­fait pas à l’idéal de Fiel­der d’une dyna­mique de 122 dB pour une repro­duc­tion subjec­ti­ve­ment exempte de bruit dans les systèmes profes­sion­nels. Accé­der à cette dyna­mique requiert une réso­lu­tion d’en­vi­ron 21 bits. Il arrive souvent qu’une certaine « marge » avant satu­ra­tion soit requise en enre­gis­tre­ment profes­sion­nel. En d’autres termes, une plage dyna­mique excé­dant le niveau d’en­re­gis­tre­ment maxi­mum nomi­nal doit être dispo­nible pour encais­ser un éven­tuel dépas­se­ment. C’est une des raisons pour lesquelles les profes­sion­nels réclament des réso­lu­tions supé­rieures à 16 bits. Le passage à une réso­lu­tion de 24 bits est aujour­d’hui forte­ment engagé même si l’éten­due dyna­mique excède les besoins psycho-acous­tiques.

Voila donc quelques premiers prin­cipes de la conver­sion analo­gique numé­rique. Pour mes fans ou ceux qui veulent aller plus loin encore, vous trou­ve­rez sur mon site perso des éléments suplé­men­taires concer­nant le suréchan­tillon­nage et le bruit de disper­sion qui sont deux nouveaux concepts assez bluf­fants.