Gabou de l aide!;)
- 91 réponses
- 12 participants
- 7 271 vues
- 1 follower
Afficher le sujet de la discussion
exusez pour l'intrusion mais Gabou tu veux dire qu' Adobe Auditon = ex Cool Edit Pro
non ?
Alerte Geek sponsorisé
Bon Gaboo on attend ton mail hein, fais pas l'con
bah allons y soyons fou...
Il est temps d'aller faire un gros dodo... 
Oh si Renzi... j'admire les mecs comme toi qui se penchent sur ces choses là! Moi j'étais plutôt abonné aux extra-terrestres de Littéraire (ah, souvenirs...
) et je voyais la zik et ses dérivés comme un art et non une science. Pourtant, pour bon nombre d'entre nous, ces deux notions sont devenues inter-dépendantes.
C'était juste une petite boutade en passant. Moi je suis utilisateur, pas chercheur.
BIG UP Renzi.
Tu nous diras comment tu les as tous pourris!
Sur ce, je vais me coucher.@+
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Anonyme
1094
Mouais ss doute..... je suis pas trop compétent pour te dire si tu sera grand matheux, mais deja bon t'es quand meme bien parti.... je suis encore en train de méditer 
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Anonyme
5238
Je sais pas si t'es fort en math ,mais en tous cas sois tu t'es pris la tete pour taper tout ca sois tu metrise grave le clavier d'ordi... 
Anonyme
1094
Anonyme
1094
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Bon, "l'équation", maintenant :
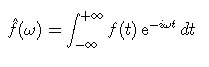
Il s'agit en fait de la définition de la transformée de Fourier d'une fonction de L2, ie des fonctions de carré intégrable. On va reprendre dans l'ordre:
Le signe qui ressemble vaguement à un S est une intégrale (S pour somme). Pour faire simple, c'est l'inverse de la dérivation. Ainsi, avec la convention que la formule du dessus peut s'écrire "f chapeau" = S(f(t)*e(-2*i*omega*t), t=-oo..oo), pour une fonction continue, on peut écrire que f(x) = dérivée de S(f(t), t=0..x) par rapport à la variable x (on écrit par rapport à la variable x car il y a plusieurs variables ici, même si formellement, la variable t n'a aucune importante ici... Dériver une fonction de par exemple deux variables x et t par rapport à t, c'est tout simplement considérer la dérivée de la fonction en x, et considérer alors que t est constant: si f(x,t) = t.x^2, alors f dérivé par rapport à x, c'est 2x.t, et f dérivée par rapport à t, c'est x^2).
Bon, on sait en général dériver les fonctions, quand c'est possible (souviens toi, toutes les fonctions ne sont pas dérivables, même si elles sont continues). Les "intégrer", plus difficilement: comme ça, de tête, t'auras du mal à me dire quelle est la fonction g tel que g' soit 1/x. C'est tellement difficile qu'on a du "l'inventer", et c'est la fameuse fonction logarithme ln : ln' = x->1/x.
L'autre vision de l'intégrale est plus géométrique, et c'est d'ailleurs celle qui prévaut en mathématiques modernes, car permettant une extentionà une classe très large de fonctions (ça a mis plus d'un siècle et demi, entre 1750 et début du XXe, avec la théorie de l'intégration de Lebesgue, capitale dans la compréhension mathématique de la transformation de Fourier). Bref, l'intégrale d'une fonction entre deux bornes a et b pour une fonction positive, c'est l'aire de la surface entre le "dessin" de f, l'axe des abscisses, entre les nombres a et b. Ainsi, l'intégfrale de la fonction x->x entre 0 et 1, c'est 1/2. En fait, l'intégrale, c'est donner un nombre à une fonction, bref, la mesurer (mesurer qqch, ça veut bien dire lui assigner un certain nombre, et dire qu'une chose est plus grosse qu'une autre si sa mesure est plus grande qu'une autre: on sait pas dire qu'une fonction est plus grande qu'une autre en général, mais on peut comparer leurs intégrales, car on sait comparer tous les nombres réels. Mesurer, c'est essentiel en physique, et d'ailleurs, la théorie de la mesure a déjà été faite en philosophie au temps des grecs, c'était d'ailleurs un point d'achoppement fondamental entre Socrate et les sophistes, mais on fait plus vraiment des maths, là ;) ).
Bon, coup de bol, quand la fonction est continue (je noterais C0 pour dire continue, maintenant), ben les deux visions, "inverse de la dérivation" et "géometrique" sont identiques.
Maintenant, revenons à la formule. Ici, les bornes sont +oo et -oo. Et la fonction intégrée est f, multipliée par une fonction "bizarre", que tu connais pas a priori. En fait, c'est simple: i, c'est le nombre complexe tel que i^2=-1, et w est la pulsation, et si on note w = 2*pi*f, ben f est la .... fréquence ! e^(i*w*t) = cos(w*t)+i*sin(w*t) par définition, et en fait, t'as qu'à te dire, comme tu connais pas les nombres complexes, je pense, que e^(i*w*t) = cos(w*t) (même si c'est complètement faux, ça te permettra quand même de comprendre la suite, sans te faire chier avec les nombres complexes, dont la compréhension n'est pas vraiment fondamentale ici).
Donc on mesure la fonction f multipliée avec la fonction cos(w*t). Je t'ai dit que l'intégrale, c'était une manière de "mesurer" la fonction à l'intérieur de l'intégrale, donc ici de mesurer f.cos(w*t). Donc "f(w) chapeau", que je note g(w) ici, est d'autaut plus grand que la mesure de f.cos(wt) est grand. Et en fait, ça revient à dire que f et cos(w*t) sont "proches". Pour mieux comprendre ça, il faudrait que tu saches ce qu'est le produit scalaire de deux vecteurs, mais je crois que ça se fait en terminale et pas en première. Mais bon, dis toi que l'intégrale mesure à quel point f et cos(w*t) sont proches (on dit aussi fortement corrélées).
Du coup, tu vois peut être le rapport entre la définition et celle que je t'ai donnée auparavant: pour w fixé, disons w0, ben g(w0) est grand (on va dire non nul ici pour simplifier) si f et cos(w0*t) sont proches, donc que les graphes de f et cos(w0*t) sont plus ou moins superposables. Du coup, quand ça se passe bien, tu peux écrire f comme intégrale de g(w) et cos(w*t), ie une somme sur tous les omega de g.cos(w*t). Donc f contient les fréquences w, là ou g(w) est non nulle; finalement, ça dit la même chose que la somme à l'infini de mon précédent post: tu écris f comme somme de cos(w*t), avec certains coefficients, et la fonction qui donne ces coefficents en fonction de w, c'est le spectre, donnée par la formule tout en haut.
Mathémtatiquement, la formle en haut, et surtout son inversion ( ie écrire f à partir d'une formule proche de celle là avec f chapeau à l'intérieur de l'intégrale) pour L2 est pas évidente du tout. En effet, pour des questions assez complexes, on est obligé d'utiliser une intégrale différente que celle "de base", dite de Riemann, qui est celle que tu verras en terminale. De plus, obtenir la formule d'inversion demande des critères assez subtiles sur la régularité de certains opérations dans des espaces assez théoriques. Moi même, je n'ai vu la définition "propre" au sens mathématique du terme de la TF que cette année, alors tu vois...
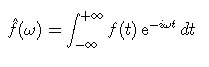
Il s'agit en fait de la définition de la transformée de Fourier d'une fonction de L2, ie des fonctions de carré intégrable. On va reprendre dans l'ordre:
Le signe qui ressemble vaguement à un S est une intégrale (S pour somme). Pour faire simple, c'est l'inverse de la dérivation. Ainsi, avec la convention que la formule du dessus peut s'écrire "f chapeau" = S(f(t)*e(-2*i*omega*t), t=-oo..oo), pour une fonction continue, on peut écrire que f(x) = dérivée de S(f(t), t=0..x) par rapport à la variable x (on écrit par rapport à la variable x car il y a plusieurs variables ici, même si formellement, la variable t n'a aucune importante ici... Dériver une fonction de par exemple deux variables x et t par rapport à t, c'est tout simplement considérer la dérivée de la fonction en x, et considérer alors que t est constant: si f(x,t) = t.x^2, alors f dérivé par rapport à x, c'est 2x.t, et f dérivée par rapport à t, c'est x^2).
Bon, on sait en général dériver les fonctions, quand c'est possible (souviens toi, toutes les fonctions ne sont pas dérivables, même si elles sont continues). Les "intégrer", plus difficilement: comme ça, de tête, t'auras du mal à me dire quelle est la fonction g tel que g' soit 1/x. C'est tellement difficile qu'on a du "l'inventer", et c'est la fameuse fonction logarithme ln : ln' = x->1/x.
L'autre vision de l'intégrale est plus géométrique, et c'est d'ailleurs celle qui prévaut en mathématiques modernes, car permettant une extentionà une classe très large de fonctions (ça a mis plus d'un siècle et demi, entre 1750 et début du XXe, avec la théorie de l'intégration de Lebesgue, capitale dans la compréhension mathématique de la transformation de Fourier). Bref, l'intégrale d'une fonction entre deux bornes a et b pour une fonction positive, c'est l'aire de la surface entre le "dessin" de f, l'axe des abscisses, entre les nombres a et b. Ainsi, l'intégfrale de la fonction x->x entre 0 et 1, c'est 1/2. En fait, l'intégrale, c'est donner un nombre à une fonction, bref, la mesurer (mesurer qqch, ça veut bien dire lui assigner un certain nombre, et dire qu'une chose est plus grosse qu'une autre si sa mesure est plus grande qu'une autre: on sait pas dire qu'une fonction est plus grande qu'une autre en général, mais on peut comparer leurs intégrales, car on sait comparer tous les nombres réels. Mesurer, c'est essentiel en physique, et d'ailleurs, la théorie de la mesure a déjà été faite en philosophie au temps des grecs, c'était d'ailleurs un point d'achoppement fondamental entre Socrate et les sophistes, mais on fait plus vraiment des maths, là ;) ).
Bon, coup de bol, quand la fonction est continue (je noterais C0 pour dire continue, maintenant), ben les deux visions, "inverse de la dérivation" et "géometrique" sont identiques.
Maintenant, revenons à la formule. Ici, les bornes sont +oo et -oo. Et la fonction intégrée est f, multipliée par une fonction "bizarre", que tu connais pas a priori. En fait, c'est simple: i, c'est le nombre complexe tel que i^2=-1, et w est la pulsation, et si on note w = 2*pi*f, ben f est la .... fréquence ! e^(i*w*t) = cos(w*t)+i*sin(w*t) par définition, et en fait, t'as qu'à te dire, comme tu connais pas les nombres complexes, je pense, que e^(i*w*t) = cos(w*t) (même si c'est complètement faux, ça te permettra quand même de comprendre la suite, sans te faire chier avec les nombres complexes, dont la compréhension n'est pas vraiment fondamentale ici).
Donc on mesure la fonction f multipliée avec la fonction cos(w*t). Je t'ai dit que l'intégrale, c'était une manière de "mesurer" la fonction à l'intérieur de l'intégrale, donc ici de mesurer f.cos(w*t). Donc "f(w) chapeau", que je note g(w) ici, est d'autaut plus grand que la mesure de f.cos(wt) est grand. Et en fait, ça revient à dire que f et cos(w*t) sont "proches". Pour mieux comprendre ça, il faudrait que tu saches ce qu'est le produit scalaire de deux vecteurs, mais je crois que ça se fait en terminale et pas en première. Mais bon, dis toi que l'intégrale mesure à quel point f et cos(w*t) sont proches (on dit aussi fortement corrélées).
Du coup, tu vois peut être le rapport entre la définition et celle que je t'ai donnée auparavant: pour w fixé, disons w0, ben g(w0) est grand (on va dire non nul ici pour simplifier) si f et cos(w0*t) sont proches, donc que les graphes de f et cos(w0*t) sont plus ou moins superposables. Du coup, quand ça se passe bien, tu peux écrire f comme intégrale de g(w) et cos(w*t), ie une somme sur tous les omega de g.cos(w*t). Donc f contient les fréquences w, là ou g(w) est non nulle; finalement, ça dit la même chose que la somme à l'infini de mon précédent post: tu écris f comme somme de cos(w*t), avec certains coefficients, et la fonction qui donne ces coefficents en fonction de w, c'est le spectre, donnée par la formule tout en haut.
Mathémtatiquement, la formle en haut, et surtout son inversion ( ie écrire f à partir d'une formule proche de celle là avec f chapeau à l'intérieur de l'intégrale) pour L2 est pas évidente du tout. En effet, pour des questions assez complexes, on est obligé d'utiliser une intégrale différente que celle "de base", dite de Riemann, qui est celle que tu verras en terminale. De plus, obtenir la formule d'inversion demande des critères assez subtiles sur la régularité de certains opérations dans des espaces assez théoriques. Moi même, je n'ai vu la définition "propre" au sens mathématique du terme de la TF que cette année, alors tu vois...
Anonyme
521397
Citation : audiophile = ex cool edit).
exusez pour l'intrusion mais Gabou tu veux dire qu' Adobe Auditon = ex Cool Edit Pro
non ?
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Anonyme
521397
Exact mais tu as tapé "Audiophile" au lieu de Adobe Audition
ne ferais tu pas de la pub déguisée subliminale pour les cartes sons MAudio
ne ferais tu pas de la pub déguisée subliminale pour les cartes sons MAudio
Fuyuhiko
26198
Vie après AF ?
Membre depuis 22 ans
Alerte Geek sponsoriséBon Gaboo on attend ton mail hein, fais pas l'con
I'm Back
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Oui, je sais
Fuyuhiko
26198
Vie après AF ?
Membre depuis 22 ans
HOHO Enfin je dissa passke qd je te vois étaler un post de 100 lignes et qu'on n'a pas un piti mail de 2, y'a comme qui dirait une alerte vexationitude tu voués
'Spèsse de keeuuuuuuukine va
Enfin je dissa passke qd je te vois étaler un post de 100 lignes et qu'on n'a pas un piti mail de 2, y'a comme qui dirait une alerte vexationitude tu voués 'Spèsse de keeuuuuuuukine va
I'm Back
Anonyme
1094
piaz
1645
AFicionado·a
Membre depuis 22 ans
Tain, Gabou, c'est beau comme tu parles
Piaz
Anonyme
1094
Me revoila apres beaucoup d'absence,
gabou, je voulais te demander pour le mp3 c'est bien la FFT qui est utilisée, ou plutot la transformée rapide de fourier ? en quoi differe t-elle de l'originale ? qu-est'ce qu'elle approrte ? quel son principe général ( en un paragraphe ;-) ) ?
J'ai aussi entendu parler de la DCT ? ca ne concerne pas le mp3 n'est-ce pas ? je crois bien que c pour le jpg...
merci encore de ton aide
gabou, je voulais te demander pour le mp3 c'est bien la FFT qui est utilisée, ou plutot la transformée rapide de fourier ? en quoi differe t-elle de l'originale ? qu-est'ce qu'elle approrte ? quel son principe général ( en un paragraphe ;-) ) ?
J'ai aussi entendu parler de la DCT ? ca ne concerne pas le mp3 n'est-ce pas ? je crois bien que c pour le jpg...
merci encore de ton aide
jambesexy
7793
Je poste, donc je suis
Membre depuis 23 ans
En attendant un réponse plus complète de gabou (qui assure 
un max!)...
si je comprends bien ta question: la transformée de fourier ne diffère en rien de l'original, ou plutôt elle ne transforme pa ton fichier wav par exemple si tu l'as appliqué dessus...c'est juste une manière fréquentielle de voir le son..
pour le mp3, comme gabou l'as dit ds son 1er post, la transformée de fourier sert à voir de quelles frequences est composé le son et donc deceler quelles frequences sont masquées par notre physiologie...
je suis pas sur ke c t bien la question posé mais bon j'aimerai faire péter mon compteur! ;)
un max!)...si je comprends bien ta question: la transformée de fourier ne diffère en rien de l'original, ou plutôt elle ne transforme pa ton fichier wav par exemple si tu l'as appliqué dessus...c'est juste une manière fréquentielle de voir le son..
pour le mp3, comme gabou l'as dit ds son 1er post, la transformée de fourier sert à voir de quelles frequences est composé le son et donc deceler quelles frequences sont masquées par notre physiologie...
je suis pas sur ke c t bien la question posé mais bon j'aimerai faire péter mon compteur! ;)
Anonyme
1094
Pov Gabou
19553
Drogué·e à l’AFéine
Membre depuis 23 ans
Anonyme
1094
Citation : Le MP3 utilise une MDCT, où le M signifie modified. Je peux t'expliquer vite fait pourquoi si tu veux...
bah allons y soyons fou...
Anonyme
1094
wijzz :8)
2053
AFicionado·a
Membre depuis 21 ans
Il est temps d'aller faire un gros dodo... Anonyme
1094
wijzz :8)
2053
AFicionado·a
Membre depuis 21 ans
Citation : Pourquoi t'es pas d'accord avec ma vision de la chose
Oh si Renzi... j'admire les mecs comme toi qui se penchent sur ces choses là! Moi j'étais plutôt abonné aux extra-terrestres de Littéraire (ah, souvenirs...
) et je voyais la zik et ses dérivés comme un art et non une science. Pourtant, pour bon nombre d'entre nous, ces deux notions sont devenues inter-dépendantes.C'était juste une petite boutade en passant. Moi je suis utilisateur, pas chercheur.
BIG UP Renzi.
Tu nous diras comment tu les as tous pourris! Sur ce, je vais me coucher.@+
- < Liste des sujets
- Charte