Différence numérique et anologique

 comment mixer dans ces conditions ?

 ben, en braille évidemment ...

Citation de Eratom

L'intérêt est d'abord de relâcher la contrainte du filtre de sortie analogie en le déportant vers le numérique.

Je sais, seulement je ne parlais pas de suréchantillonnage à la conception mais d'utilisation par exemple de DACs permettant d'écouter soit avec la Fe du fichier, soit en suréchantillonnant, et même dans certains cas en pouvant choisir la forme du filtre (un afien parlait du Denon DA-300 il n'y a pas longtemps et j'ai vu cela en regardant les specs de la bête).

D'ailleurs quand on regarde le spectre en sortie analogique d'interfaces audio à l'oscilloscope (donc montant plus haut en fréquence qu'une carte son) on constate souvent qu'il y a eu suréchantillonnage en interne, cf. exemple ici.

Hors sujet :

Celui-ci ?

Non, j'ai dû me tromper de référence. Il y avait en FAV le choix du type de filtre, de mémoire phase linéaire (Bessel) et je ne sais quoi, et un compte-rendu de test d'écoute comparatif avec ces filtres. Et cela m'avait laissé quelque peu dubitatif.

Edit : mais celui-ci est pas mal gratiné !

Edit2 : c'était le Cambridge DacMagic Plus

Citation de nujazzbes

 Juste pour une petite précision le vinyle c'est de l'analogique ou du numérique ?

 Le disque vinyl peut très bien être les deux à la fois .Il existe des disques vinyl qui sont fait d'après un enregistrement qui lui a utilisé une console numérique .

Perso ,ce qui me gênerait plus que la bande passante ,c'est le non respect de la phase .Et justement dans les convertisseurs a/n ,il y a un méchant problème de phase dont personne ne parle jamais :elle joue au yoyo selon les fréquences .Ca doit être dû probablement à Nyquist/Shanon qui n'utilise pas une echelle linéaire ,mais logarythmique ,mais je suis bien incapable de la prouver .Pour le prouver ,il faudrait un convertisseur à échelle linéaire ...Et faire des comparaisons .

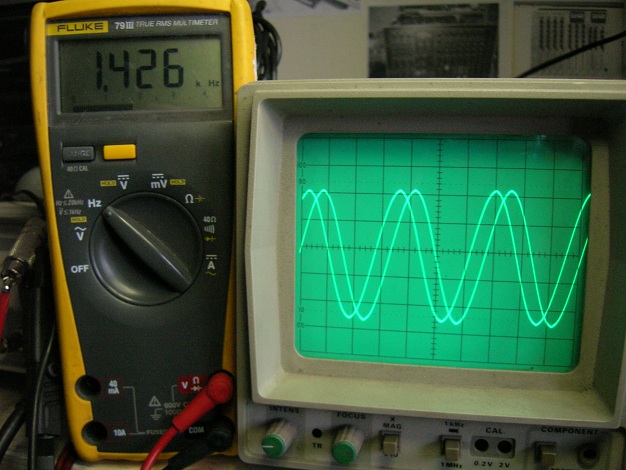
La seule chose que j'ai mesurée ,c'est ce déphasage dans un converto (44.1k / 24bits) : ça se déphase (comme la photo ci-dessous) ,puis ça se recale bien (à une autre fréq),puis ça se redéphase (à une autre fréq) etc.... Et j'aime pas ce genre de signal .En analogique ,on a pas ça dans un système conçu correctement .Et personne n'en parle jamais de ce

problème ...

Citation de jan

 Ce que tu observes ne serait pas plutôt un retard contant qui effectivement, observé sur un sinus glissant et comparé au signal non retardé pourrait laisser penser qu'on a affaire à un dėphasage.

 C'est possible ,mais quelques centaines de Herts plus haut ,il n'y a plus de déphasage ,puis quelques centaines de hertzs encore plus haut ça se redéphase ,etc ,etc .J'ai jamais vu ça avant .Ce déphasage est mesuré entre l'entrée et la sortie du converto'.C'est possible que ça soit un sinus glissant qui repasse par zéro ,puis reglisse etc...Mais c'est très curieux à voir.

Citation de nujazzdes

 Il y explique que le vinyle peut renvoyer des fréquences allant de 50 Hz à 16000 Hz ; contrairement au cd qui lui peut aller de 20 Hz à 20000 Hz ! Ainsi le vinyle aurait un son plus chaud puisqu'il reproduit moins de haute fréquence.

 Mes vinyls non usés passent de 30hz à 20khz à 3dB .Faut pas oublier un truc :le vinyl plus on le passe à lire ,plus il va perdre des aigus .En général ,on dit passé une cinquantaine de fois ,on commence à perdre dans le haut .

Pour mesurer la bande vinyl ,j'utilisais un disque vinyl avec des fréquences gravées de 20hz à 20khz .

Citation de philrud

problème ...

Je crois surtout que c'est l'un des nombreux pièges des mesures sur signaux répétitifs.

Comme cela me semblait bizarre (l'écart correspond à # 4.5 échantillons !) j'ai fait la même manip sur une Babyface.

Avec un sinus je trouve la même chose.

Avec une impulsion courte je retrouve le même phénomène mais la forme en sortie est la bonne réponse impulsionnelle (donc pas de problème de phase).

En déclenchant par l'oscilloscope (envoi de l'impulsion) et non plus par le signal, je constate que le retard est beaucoup important (donc changement d'échelle des temps) et constant, ce qui est normal.

Par conséquent le problème est une sorte de phénomène de repliement visuel puisque l'on déclenche sur un signal répétitif de période plus courte que le retard.

Edit : et pour répondre à la question initiale, dans ce cas précis la différence entre numérique et analogique est la latence.

Citation de nujazzbes

 Il y explique que le vinyle peut renvoyer des fréquences allant de 50 Hz à 16000 Hz ; contrairement au cd qui lui peut aller de 20 Hz à 20000 Hz ! Ainsi le vinyle aurait un son plus chaud puisqu'il reproduit moins de haute fréquence.

 J'ai vu la vidéo et je dis attention ! Attention à la réponse ,car ce n'est peut-être pas aussi évident que ça en a l'air ...Car quand on écoute une musique que ça soit vinyl ou cd ,il y a d'abord le son masterisé (son du disque,de l'album),puis le matériel d'écoute .

J'ai fait à plusieures reprises des tests d'écoute entre le même disque (même album),l'un en vinyl ,l'autre en cd :j'étais incapable de dire lequel était le mieux .Les 2 albums (cd ou vinyl) sonnaient pareil à l'écoute .J'ai l'impression que c'est surtout le son de l'album qui compte .

Par contre ,comme dit dans la vidéo ,depuis les années 90's on a tendance à gonfler les décibels par des boosts exagérés sur les cd's et là :ça me gonfle les oreilles ,je déteste .C'est peut-être pour ça que certains préfèrent le polychlorure de vinyl .

Encore par contre ,il y a aussi en vinyl dans les 45trs certains disques qui étaient gonflés dans le médium (années 80's) , et là aussi je trouvais ça mauvais .

Pour moi ,vinyl ou CD ,c'est pas ce qui compte , c'est pas le problème ,mais c'est bien tout l'enregistrement qui compte prise,mix,master qui comptent beaucoup plus .D'ailleurs (je le répète) un album vinyl qui sonne super bien,c'est "indiana Jones et le temple maudit" et quand on lit sur la pochette du vinyl ,on voit "prise de son et enregistrement numériques".Et là je me marre bien ,quand il y en a qui disent "Ouais ! Ah ça sonne bien le vinyl !" .Quoi que faut se méfier là encore ...Il y a le pressage , que peut-il se passer au pressage et à la lecture qu'on aurait pas dans le Master d'origine ... 

 Ainsi le vinyle aurait un son plus chaud puisqu'il reproduit moins de haute fréquence.

 Je trouve cette phrase un peu grosse ,ça n'a aucun rapport .A l'époque mon préampli phono ne passait que le 15khz ,mais montait en 0,2µs et surtout avait une "patate" d'enfer à tel point que je trouvais les premiers CD du commerce bien mous à côté.D'ailleurs les premiers lecteurs CD aussi ne passaient pas plus que le 17khz et sur certains lecteurs (BST CD235) on entendait même en fond un résidu de fréq. d'échantillonnage ...Les choses se sont améliorées depuis ,heureusement .

Je vais même en rajouter une couche ,puisque ce CD BST 235 tournait même en Radio à l'époque parce que ce lecteur avait un son naturel à l'écoute :il n'utilisait pas de quartz dans l'horloge ,le son en était même limite chaud .Pour dire que analogique ou numérique ,ça dépend de tellement de choses ...

 ce n'est pas physiquement possible.

C'est comme :

Et justement dans les convertisseurs a/n ,il y a un méchant problème de phase dont personne ne parle jamais

 Et pour cause, c'est faux !

Citation de jimbass

 

Hors sujet :

Et est-ce que tu pourrais, s'il te plaît, essayer d'appliquer les règles de ponctuation ? Ca rendrait tes posts bien plus lisibles.

 Tu plaisantes là ,rassure moi ?

 Je ne comprends pas où tu veux en venir avec ces histoires de vinyle "à moité numérique". 

 Ben ici le sujet c'est analogique / numérique :on est bien d'accord ...Alors le vinyl qui d'apparence est analogique ,peut contenir du signal numérique (mixage par ex )qui a été converti en analo' forcément pour la gravure .Si pour toi ,seul le dernier support compte (ici le vinyl) ,c'est pas le cas pour tout le monde ...