Si l'on a coutume de dire que la musique est un langage, l'on peut considérer qu'elle est constituée de phrases, et que les cadences en représentent en quelque sorte les ponctuations.
Dans cet article, nous allons revenir d’abord sur la cadence parfaite que nous avons évoquée précédemment, puis nous allons étudier les autres principales formes de cadences qui existent.
La cadence parfaite
Comme nous avons commencé à le voir dans les articles précédents, non seulement chaque degré d’une gamme possède une fonction précise, mais le degré V suivi du degré I forment une cadence parfaite qui sert bien souvent à clore un morceau, ou du moins une phrase musicale.
Petit aparté, pour illustrer l’importance historiquement particulière de ces degrés de la gamme. Entre le 5e et le 6e siècle de notre ère, le philosophe Boëce prône l’utilisation de rapports mathématiques simples 2:1 ou 3:2 dans l’architecture et la musique. La musique est considérée à cette époque comme la science qui modèle le monde, affectant d’ailleurs positivement ou négativement jusqu’à la santé même de l’être humain. Or, les rapports 2:1 et 3:2 correspondent aux rapports entre la note fondamentale et ses premières harmoniques supérieures, l’octave (2:1) et la quinte (3:2), donc le Ier degré et le Ve (sur les harmoniques, voir l’article 3 du dossier sur la synthèse sonore : Les fréquences).
La cadence parfaite servant souvent, je le répète, à clore une phrase musicale ou bien un morceau entier, on peut alors considérer que, rapportée au langage écrit traditionnel, celle-ci correspondrait à un point. La cadence parfaite représente donc — comme son nom le laisse deviner — la forme de cadence la plus importante.
Petite précision : dans le cas d’une cadence parfaite, on dit aussi que l’accord de dominante fait une approche pour atteindre l’accord de tonique de la gamme. Et pour renforcer l’effet de cette « approche », on emploie souvent l’accord de septième de dominante à quatre notes plutôt que l’accord majeur à trois notes (voir article 4). Nous verrons dans un futur article la raison de ce « renforcement ».
Dans les exemples qui vont suivre, et pour vous habituer petit à petit aux renversements d’accords, tous les exemples suivants seront constitués d’une ligne mélodique dans la partie supérieure, harmonisée par des accords au second renversement, sauf l’accord final de chaque phrase musicale qui sera dans sa position fondamentale. La seule forme de cadence qui dérogera à cette « règle » sera l’« anatole », afin de conserver sa signature sonore caractéristique. Je vous laisserai d’ailleurs repérer par vous-même les accords renversés !
Mais revoyons déjà ici l’exemple d’une cadence parfaite majeure :
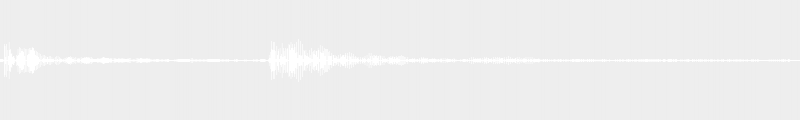
La demi-cadence
Une forme particulière de la cadence parfaite est la demi-cadence. On pourrait la définir non plus comme un point, mais plutôt comme une virgule, car elle ne marque pas la fin d’une phrase musicale, mais sert plutôt à relancer le discours. On l’appelle également « cadence à la dominante » car elle ne mène pas à la tonique, mais… à la dominante. On la trouve aussi souvent précédent une cadence parfaite.
Dans l’exemple suivant, on a d’abord la demi-cadence seule, puis la demi-cadence suivie d’une cadence parfaite. À noter que concernant la demi-cadence, le degré qui mène vers le V n’est pas obligatoirement le IV. Mais c’est tout de même ce dernier que j’ai gardé dans l’exemple suivant pour conserver une cohérence avec l’ensemble des exemples de l’article.
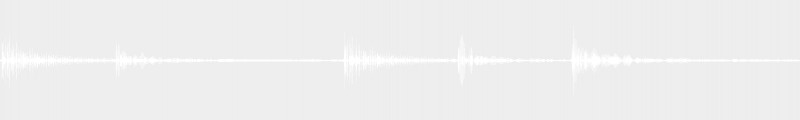
La cadence plagale
Nous avons ensuite la cadence dite « plagale », qui se définit par un passage du IVe au premier degré de la gamme. Celle-ci porte en elle un caractère beaucoup moins fort que la cadence parfaite, et n’est que très peu usitée seule pour terminer un morceau. Par contre, elle peut servir pour accentuer encore la fin cadence parfaite finale d’un morceau.
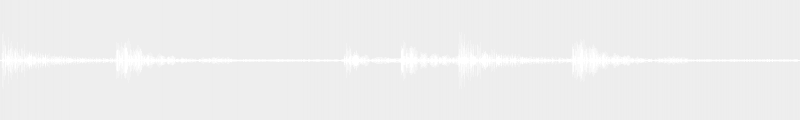
L’anatole
L’une des plus célèbres formes de cadences est l’« anatole ». Elle est composée d’un enchaînement des degrés VI, II, V et I sous la forme… VI-II-V-I ou bien sous la forme I-VI-II-V (qui réaboutit au I la plupart du temps).
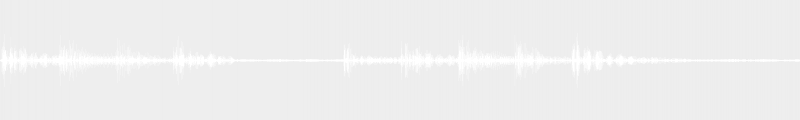
À noter que l’on peut également considérer l’anatole comme une chute (une cadence !) de quinte juste inférieure en quinte juste inférieure à partir du degré VI de la tonalité du morceau, et jusqu’à la tonique.
La cadence rompue
Enfin, nous avons la cadence dite « rompue » ou « évitée », qui se différencie de la cadence parfaite en ce qu’elle ne mène pas au premier degré, mais au VIe. On a donc dans ce cas-là une progression V-VI. Elle n’achève pas le morceau (d’où son nom de cadence rompue), mais permet de l’orienter sur une couleur harmonique différente, souvent bienvenue avant d’achever réellement la pièce musicale. Et, dans le cas d’une tonalité majeure, cette couleur harmonique n’est d’ailleurs rien d’autre que… celle de la relative de la tonalité du morceau, puisque le VIe degré d’une gamme donnée correspond au Ier degré de la relative mineure de cette même gamme !
À noter que la cadence rompue de l’exemple précédent, en menant le morceau vers le degré VI de la tonalité, peut faire basculer ce dernier dernier dans la tonalité de sa relative mineure, ici La mineur. Ceci est un exemple typique de « modulation », ce qui en jargon harmonique signifie l’utilisation d’un degré issu d’une gamme donnée pour passer à l’utilisation d’une autre tonalité. Nous étudierons les modulations de manière plus approfondie dans un futur article.
La semaine prochaine, pour poursuivre notre quête de la juste harmonisation, je vous propose de comprendre ensemble comment définir quelles notes appartiennent à quels accords et à quelles tonalités, à travers l’étude des notes « réelles » et des notes « étrangères ».





