Le spectre dans la synthèse FM - La synthèse sonore - 22e partie

Des maths et des fréquences

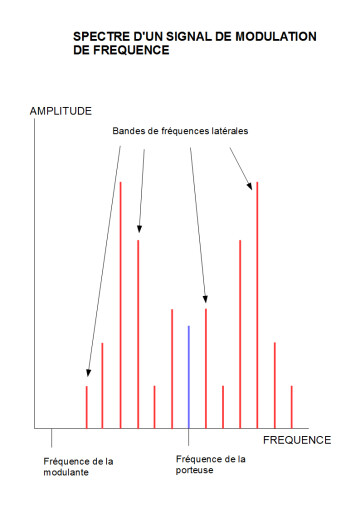
Le spectre harmo­nique dépend du rapport entre la fréquence de la porteuse et celle de la modu­lante. Si P/M est un nombre entier, les fréquences produites seront des harmo­niques des deux fréquences P et M. Si P/M n’est pas un nombre entier, le spectre sera inhar­mo­nique. Le compo­si­teur Barry Truax (voir article précé­dent) a d’ailleurs classé les diffé­rents rapports P/M produits par la synthèse FM en diffé­rentes grandes familles de sono­ri­tés, afin d’en faci­li­ter l’uti­li­sa­tion.

Après la nature du spectre harmo­nique du signal se pose la ques­tion de sa largeur de bande. Pour rappel, la largeur de bande d’un signal repré­sente l’en­semble des fréquences que celui-ci comporte. Dans le cadre de la synthèse FM, la largeur de bande dépend inté­gra­le­ment de ce que l’on appelle l’in­dex de modu­la­tion (« I »). Celui-ci s’ob­tient par la formule I=D/M où D symbo­lise la quan­tité de dévia­tion fréquen­tielle ou profon­deur de modu­la­tion appliquée à la porteuse, et M la fréquence de l’onde modu­lante. Pour faire simple : l’in­dex de modu­la­tion traduit le degré de modu­la­tion subie par la porteuse. 

Enfin, l’am­pli­tude de chaque fréquence au sein du signal est déter­mi­née par une fonc­tion mathé­ma­tique, dite « de Bessel ». Sans entrer dans des consi­dé­ra­tions mathé­ma­tiques qui dépas­se­raient le cadre de cet article, souli­gnons seule­ment que cette fonc­tion, qui intègre l’in­dex de modu­la­tion dans l’équa­tion, induit, dans le cadre de la synthèse FM, deux compor­te­ments très inté­res­sants du signal sonore. Le premier est que l’am­pli­tude maxi­male et la puis­sance du signal n’ont pas à varier avec l’in­dex de modu­la­tion. Vous pouvez faire varier « I » autant que vous voulez, cela n’af­fec­tera pas le volume global du signal. L’autre carac­té­ris­tique d’un signal sonore produit par synthèse FM est que, plus on augmente l’in­dex de modu­la­tion, plus l’am­pli­tude de la fréquence de P, au sein du signal géné­ral, dimi­nue au profit de celle des bandes laté­rales. Elle peut même dispa­raître tota­le­ment, ce qui rapproche alors la modu­la­tion de fréquences de la modu­la­tion en anneau (voir article 14), mais avec un nombre de bandes laté­rales beau­coup plus impor­tant. 

 

La synthèse FM – où et quand ?

Comme nous l’avons vu, si la synthèse FM n’est pas inima­gi­nable dans le monde analo­gique – John Chow­ning, son « décou­vreur », a d’ailleurs été le premier, en 1966, à compo­ser une œuvre inté­gra­le­ment exécu­tée en synthèse FM analo­gique – c’est prin­ci­pa­le­ment dans le domaine numé­rique qu’elle a trouvé son épanouis­se­ment. Et c’est Chow­ning, toujours lui, qui a été le premier à expé­ri­men­ter l’im­plé­men­ta­tion numé­rique de sa décou­verte. Après qu’il a déposé un brevet au début des années 70 et vaine­ment cher­ché auprès des entre­prises améri­caines des débou­chés indus­triels à ses recherches, c’est fina­le­ment Yamaha qui se montre inté­ressé par son travail.

L’en­tre­prise japo­naise va déve­lop­per et amélio­rer les prin­cipes énon­cés par Chow­ning, et va présen­ter en 1980 le synthé­ti­seur numé­rique GS 1, puis, surtout, le DX7 en 1983. Son tarif démo­cra­tique pour l’époque (autour de 10 000 FF tout de même), son excep­tion­nelle stabi­lité due à sa nature numé­rique ainsi que la totale nouveauté des sons qu’il propose en feront un succès plané­taire. On le retrou­vera dans nombre de produc­tions des plus grandes stars de l’époque, de Phil Collins à Michael Jack­son en passant par Madonna et même notre Gold­man natio­nal. Yamaha pour­sui­vra d’ailleurs la série avec une demi-douzaine de modèles, dont le plus célèbre sera le DX7–2.

Native Instru­ments a émulé le DX7 en version logi­cielle avec son FM7, devenu FM8 depuis 2006. On peut égale­ment trou­ver un émula­teur open-source, DEXED.

Enfin mon âme de geek ne résiste pas à l’évo­ca­tion d’un autre champ d’ap­pli­ca­tion de la synthèse FM : celle des toutes premières cartes son, les Adlib et autres Sound Blas­ter ! En effet la richesse harmo­nique des signaux que la synthèse FM peut produire se prêtait parfai­te­ment (oui bon, pour l’époque…) à la créa­tion de toutes sortes d’ef­fets sonores pour les jeux vidéo.

Sans comp­ter qu’un certain nombre d’entre nous – dont votre servi­teur, sur un austère, mais atta­chant Amstrad PC 1512  – ont égale­ment décou­vert, par ce biais, une MAO qui se libé­rait enfin de la « tyran­nie » des Atari et autres Amiga, non, mais ! 

Conclu­sion

La synthèse FM a connu son heure de gloire grâce à la possi­bi­lité qu’elle offre de créer des sons extrê­me­ment riches à partir d’un nombre réduit d’os­cil­la­teurs/opéra­teurs, offrant ainsi, elle aussi, une alter­na­tive sédui­sante à la synthèse addi­tive, trop gour­mande en ressources.

Or la puis­sance du maté­riel numé­rique ayant augmenté, la synthèse addi­tive est deve­nue beau­coup plus simple à produire que par le passé, sans parler de la synthèse granu­laire ou bien la synthèse par modèle physique que nous étudie­rons dans les prochains articles. 

De plus, la synthèse FM est connue pour être assez peu intui­tive, et provoquer des résul­tats très diffé­rents à partir d’in­fimes modi­fi­ca­tions de para­mètres. C’est l’une des raisons (avec le grand nombre de para­mètres à gérer) pour lesquelles la synthèse FM a été très peu implé­men­tée dans des systèmes analo­giques : les oscil­la­teurs analo­giques (VCOs, voir article 6 de cette série) ne sont pas suffi­sam­ment stables pour cette forme de synthèse, capable de « partir en sucette » — comprendre : géné­rer des bandes laté­rales à foison — à la moindre varia­tion de fréquence de l’un des opéra­teurs. Mais c’est aussi ce qui pour­rait en repré­sen­ter le charme aux yeux de certains expé­ri­men­ta­teurs fous parmi vous, je le sais !

Enfin, rappe­lons que la synthèse FM ne concerne pas unique­ment les instru­ments dédiés, tels que le DX7, mais égale­ment tout synthé analo­gique dont la sortie d’un oscil­la­teur peut être commu­tée à l’en­trée CV d’un autre… Petite piste de réflexion… Sur ce, je vous donne rendez-vous au prochain article !