Fondamentale manquante : explications, débat, application pratique...
- 99 réponses
- 9 participants
- 19 715 vues
- 9 followers
Dr Pouet
je reste assez prudent sur la démarche: ça me dérange un peu de vouloir extraire des composantes d'une forme d'onde
Je comprends que toi aussi tu estimes qu'un analyseur de fréquences est nécessaire, et qu'il est trompeur de le faire à l'oeil sur la forme d'onde. C'est bien ça ?
on veut seulement "retrouver" des composantes que l'on a déjà calculées ou mesurées
Oui. Et d'ailleurs la courbe en pointillés orange ne correspond pas à une fréquence contenue dans le signal. (= la fameuse fondamentale "imaginée" par l'oreille, mais qui n'est pas dans le signal).
Si on passe ce signal dans un analyseur spectral, on va avoir une raie à 2f une autre à 3f, et aucune raie à f (son résultant), ni même f/2 (fréquence du battement). Un battement n'est pas une composante du signal.
tu parles pour 2f + 3f ou 3f + 4f ?
Je répondais à ton message juste au-dessus :
si tu fais avec 3f et 4f ça doit donner encore autre chose :
comme 2 x sin 7/2f x cos 1/2f
à f = 100 hz ça doit faire : 2 x sin 350 x cos 50
"cos 50" => 50Hz = la fréquence du battement = le pointillé "mathématiquement".
Je rappelle le truc :
- l'oreille peut percevoir un battement comme si c'était une sinusoïde (=composante) présente
- et dans ce cas, n'étant pas sensible à la phase, l'oreille croit que cette sinusoïde perçue est le double de la fréquence du battement
50Hz x 2 = 100Hz c'est le double de la fréquence dans le cosinus (on passe de 1/2f à f).
Et pour repartir de ta question : ça marche avec 2f + 3f, mais aussi avec 3f + 4f. Tant qu'on a f comme différence, ça marche.
Si on reprend le schéma :
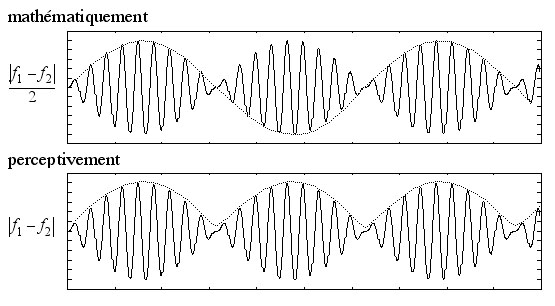
si f1 (du schéma) = 2f (de papaze)
et si f2 = 3f
Mathématiquement :
|(f1-f2)|/2 = f/2 c'est bien ce qu'il y a dans ton cosinus.
Perceptivement :
|(f1-f2)| = f , les fameux 100Hz, la fameuse différence de fréquence évoquée par Alain.
Anonyme
Hors sujet :
Citation :
Par contre en relisant le sujet d'Alain hier, j'ai pris conscience qu'on l'a vraiment pourri, qu'on aurait dû créer ce thread beaucoup plus tôt. Et donc qu'on aurait dû suivre ton conseil xheindrichs, puisque tu en avais fait la suggestion.
Ouais, ce sujet a malheureusement été fort pourri, et a dû nuire à son projet... C'est vraiment dommage. Je ne me rappelle plus quand j'avais fait cette suggestion. En fait, j'aurais dû l'ouvrir, tout simplement!
A bientôt 
Xa
Anonyme
Avec Alain DX7 nous avons fait l'expérience comme prévu.
un son composé de la somme de 2 sinus 2f + 3f
Alain DX7 entend un son "rugueux" à la fréquence f, moi je ne l'entends pas mais je n'ai pas la perception d'un musicien comme Alain.
Alain est d'accord que dans la somme 2f + 3f il n'y a pas et qu'il ne peux pas y avoir de fondamentale f.
Par contre 2f + 3f est periodique à la fréquence f.
Comme notre système auditif est bien plus qu'un analyseur de spectre je "suppose" qu'il arrive à extraire l'information que représente la fréquence f de ce signal est qu'il reconstruit congintivement une sinus approximative donnant ainsi la sensation d'un fondamentale. L'extraction de cette info est facile à faire : sur le graphique ci-dessous, f est représenté par la distance qui sépare 2 pics du signal
sur le graphique suivant le signal est 2f + 2,1f et on voit et on entend un joli battement à 0,1f = 2,1f-2f
mais il n'y aucune fondamentale à 0,1f seulement une envelloppe qui a la forme d'une sinus que le système auditif va reconstruire et donner une sensation de son à 0,1f
la différence avec le graphique à 2f + 3f c'est la quantité d'informations : c'est comme si on avait échantillonné la fondamentale. A 2f + 2,1f on a la fréquence + la forme (envelloppe), à 2f + 3f il ne reste que la fréquence la forme à disparu. Violà pourquoi moi j'entends rien : mon système auditif n'est pas assez développé.
Un test en aveugle confirmerai ma thèse, je vais tenté d'en préparer un.
[ Dernière édition du message le 02/08/2010 à 11:22:10 ]
yohda
Apparement, nous ne sommes pas tous égaux pour la perception du spectre, mais on retourne dans la neurologie là 
:
Citation :
Research conducted at Heidelberg University, as described in the January 2006 issue of the German audiophile magazine AUDIO, indicates that the general population can be divided into those who perceive missing fundamentals, and those who primarily hear overtones. The magazine article states that the difference between the perceived pitches can be up to 4 octaves.
http://www.worldlingo.com/ma/enwiki/en/Missing_fundamental/1
Citation :
Abstract
The relative pitch of harmonic complex sounds, such as instrumental sounds, may be perceived by decoding either the fundamental pitch (f0) or the spectral pitch (fSP) of the stimuli. We classified a large cohort of 420 subjects including symphony orchestra musicians to be either f0 or fSP listeners, depending on the dominant perceptual mode. In a subgroup of 87 subjects, MRI (magnetic resonance imaging) and magnetoencephalography studies demonstrated a strong neural basis for both types of pitch perception irrespective of musical aptitude. Compared with f0 listeners, fSP listeners possessed a pronounced rightward, rather than leftward, asymmetry of gray matter volume and P50m activity within the pitch-sensitive lateral Heschl's gyrus. Our data link relative hemispheric lateralization with perceptual stimulus properties, whereas the absolute size of the Heschl's gyrus depends on musical aptitude.
https://www.nature.com/neuro/journal/v8/n9/abs/nn1530.html
[ Dernière édition du message le 02/08/2010 à 11:33:42 ]
Anonyme
Anonyme
j'ai comencé hier soir à lire les documents en ma possession écrit par J CHOWING, l'inventeur de la synthèse FM.
C'est en anglais et bien sur c'est très technique. Donc ça va prendre un peu de temps.
Quand j'aurai assez avancé je ferai part de mes impresssions. Je pense ouvrir un fil spécifique pour ne pas tout mélanger.
1ere confirmation : les équations de J CHOWING sont de la modulations de phase alors pourquoi avoir appelé
cela FM au lieu de PM. Peut être çà sonne mieux commercialement
yohda
Citation :
1ere confirmation : les équations de J CHOWING sont de la modulations de phase alors pourquoi avoir appelé
cela FM au lieu de PM. Peut être çà sonne mieux commercialement
Oui, je pense que c'est la raison, la phase c'est déjà quelque chose de moins connu du grand public et à cette époque les musiciens manipulaient surtout la synthèse soustractive.
J'imagine que Yamaha et Chowning ont voulu presenter les choses le plus simplement possible.
Anonyme
Dr Pouet
Comme notre système auditif est bien plus qu'un analyseur de spectre je "suppose" qu'il arrive à extraire l'information que représente la fréquence f de ce signal est qu'il reconstruit congintivement une sinus approximative donnant ainsi la sensation d'un fondamentale. L'extraction de cette info est facile à faire : sur le graphique ci-dessous, f est représenté par la distance qui sépare 2 pics du signal.
Si je ne m'abuse, vous avez fait l'expérience de ce qui est décrit dans l'article sur le son résultant. On est d'accord ?
Vous avez l'air de ne pas vouloir reprendre la terminologie de l'article, alors qu'elle me semble pourtant plus rigoureuse, et du coup plus facile à manipuler / ré-utiliser. Le phénomène est :
- l'oreille perçoit un battement comme s'il y avait une composante
- et comme l'oreille n'est pas sensible à la phase, elle croit que cette composante est d'une fréquence double de celle du battement.
Texto :
En acoustique, un son résultant (appelé aussi un son différentiel ou concomitant) est un son produit par deux autres par le phénomène de battement[1].
Il s'agit d'un troisième son (ou une note de musique), parfaitement audible, bien que notablement plus faible, produit par l'interférence des deux premiers, et correspondant à leur différence acoustique.
La fréquence du battement est : (|f1 - f2|)/2
(= la moitié de la valeur absolue de la différence des 2 fréquences)
La fréquence perçue est = |f1 - f2|
(= la différence des 2 fréquences, toujours en valeur absolue).
il arrive à extraire l'information que représente la fréquence f
C'est juste, mais la formulation pourrait laisser croire qu'il y a une composante de fréquence f.
Toujours pour pinailler un peu mais essayer d'être rigoureux, l'œil est un peu trompeur, et je pense que ce signal n'est pas de fréquence f, mais f/2, conformément à la somme de sinus.
Accessoirement, on pourrait aussi considérer ce signal comme étant de fréquence f/4 f/6 f/8 f/12... Mais normalement on appelle "fréquence" la fréquence la plus élevée contenant une oscillation complète. Le raisonnement est plus intuitif en se basant sur la période : on appelle "période" T la durée la plus courte contenant une oscillation complète. Et la fréquence est l'inverse de la période.
Après ces pinaillages (pas fondamentaux, je le reconnais), reste à vous féliciter pour le débat constructif, pour cette rencontre "in real life" d'AFiens de Bordeaux etc...
[ Dernière édition du message le 02/08/2010 à 14:32:32 ]
plutonak
- < Liste des sujets
- Charte