J'aime autant vous prévenir tout de suite, le présent article pourra peut-être sembler un peu ardu à certains. Mais si vous avez suivi tous les autres articles jusqu'à présent, vous devriez avoir toutes les cartes en main pour comprendre ce qui suit. Sinon, n'hésitez pas à pos(t)er des questions dans les commentaires !
Qu’est-ce que l’enharmonie ?
Pour commencer, nous avons besoin d’une petite définition de l’enharmonie. Celle-ci désigne le fait de dénommer de manières différentes une seule et même note, Ré# et Mib par exemple. A noter que cette identité de note n’est valable que sur les instruments dits tempérés (les instruments à clavier ou encore les instruments à cordes frettés par exemple). Les instruments non tempérés (voix humaine, violon, basse non-frettée, trombone…) permettent de différencier éventuellement le Ré# du Mib cités plus haut. Cette petite précision effectuée, voyons comment nous pouvons l’adapter dans les faits.
L’accord de sixte augmentée
Un accord riche en possibilités de modulation enharmonique est l’accord dit « de sixte augmentée », basé sur l’accord de sixte. Attention, il ne faut pas confondre ce dernier avec un accord de sixième type CM6 (cf article XX). La dénomination « sixte augmentée » se réfère ici à la méthode de chiffrage classique – sur laquelle nous reviendrons dans un prochain article – et dans laquelle l’accord de sixte désigne le premier renversement d’un accord à trois notes. Pourquoi « de sixte » ? Parce que dans cette position-là, il y a une sixte d’intervalle entre la note la plus basse et celle la plus élevée de l’accord.
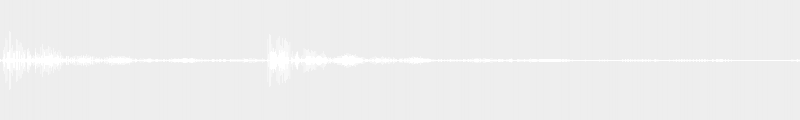
Ainsi, dans le dernier exemple, nous avons l’accord Sol-Si-Mi, qui est le premier renversement de l’accord Mi-Sol-Si (accord de Mi mineur). L’accord Sol-Si-Mi# est donc l’accord de sixte augmentée. Il est enharmonique de Sol-Si-Fa, accord de septième de dominante (sans la quinte) de la tonalité de Do. On peut ainsi passer facilement de la tonalité de Mi mineur, en faisant glisser d’un demi-ton de Mi vers Mi# (Fa enharmonique) pour construire un accord de sol dominante 7 et passer donc ainsi en tonalité de do.
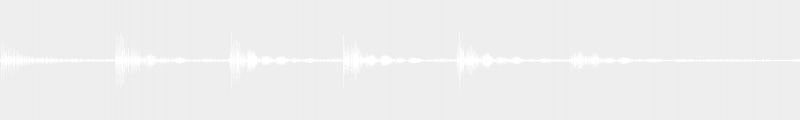
L’accord de septième diminuée
Une autre manière d’illustrer le rôle de l’enharmonie dans les modulations tonales se fera par l’emploi de l’accord de septième diminuée, dont nous en avons un exemple ci-dessous :
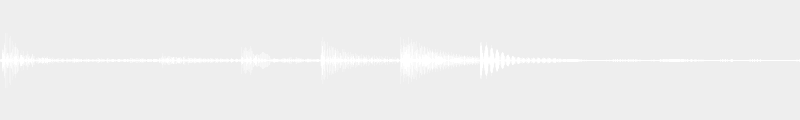
Contrairement aux autres accords, il est composé exclusivement de tierces mineures, avec un intervalle de seconde augmentée lorsque l’on enchaîne les arpèges comme dans l’exemple précédent. Ceci a pour effet que chacun de ses renversements peut correspondre à une nouvelle position fondamentale (cf article XX). Il permet donc de moduler dans quatre tonalités différentes !
Mais quel rapport avec l’enharmonie, allez-vous me dire ? Les notes de l’accord sont nommées différemment selon le « renversement » employé. À la base, cet accord est l’accord de septième de la sensible des gammes mineures harmoniques (cf article XX). Chacun de ses « renversements » correspond à l’accord de septième de la sensible d’un nouvelle gamme mineure. L’orthographe de l’accord change donc afin de respecter le diatonisme de la nouvelle gamme. Vous suivez ? Le petit exemple ci-dessous vous aidera à y voir plus clair :
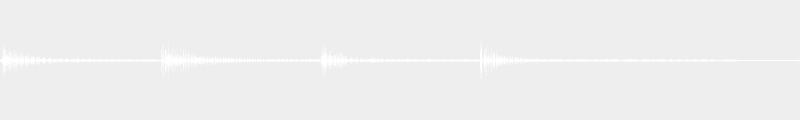
Ici, le premier accord correspond à la sensible de la gamme de La mineur harmonique, alors que le second accord – « renversement » du premier ! – correspond à la sensible de la gamme de Do mineur harmonique. L’enharmonie se situe au niveau des notes Sol # et Lab des accords respectifs.




