Sujet DEBAT : est-ce qu'on a moins de profondeur/niveau avec un mix seulement software/ordi?

Citation :

bullshit

Voici l'illustration :

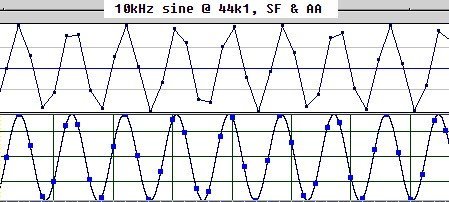
On voit bien que les échantillons se décalent au fur et à mesure que les périodes se déroulent, au bout d'un certain temps qui est égale à 1/((Fe/2)- fsamplé) la période cyclique est terminée, le filtre reconstruira parfaitement la sinusoïde.

Certes on est habitué à une approche fréquencielle de l'échantillonnage, mais là on parle de réprésenation temporelle, avec des fréquences générées ayant une durée finie

En labo on envoi une fréquence sur un GBF et les fréquence sont générées à "l'infini". Il donc plus facilement possible d'oublier que les fréquences sont générée pendant une durée finie, telle une note en musique.

Citation :

Ça doit dépendre de la position des points. S'ils sont aux sommets positifs et négatifs de la sinusoïde, c'est tranquille, sinon il doit y avoir plein de solutions.

 

Faut arreter là ... Avec deux points , on ne sait pas à quoi ressemble le signal, ça peut être une rampe , un signal carré, un signal continu, un pulse, la barbe à will zégal etc etc .... et la fréquence ca peut être tout et n'importe quoi ...

Ce n'est qu'avec un certain nombre de périodes que le signal se définie, grace à la "marche" des échantillons

Ce qui est marrant c'est  d'essayer de voir ce qui se passe si on essaye d'échantillonner la fréq 22050 avec une FE de 44,1 kHz :

On obtient deux points par période mais le temps entre ces deux échantillons est exactement égale à 1/2 période de 22050 Hz (22,6us), donc ceux-ci seront toujours positionnés au même endroit, fixes (qui se définie en degré) sur l'alternance de la sinusoide. On atteint alors la limite du process, il est impossible de reconstruire quoique ce soit, car la marche des échantillons s'arrête.

C'est un autre cas de figure ou l'on a deux points et l'on ne peut pas reconstruire la sinusoïde, même si la fréquence est générée à l'infini. 

Le cas F = FE / 2 est particulier. Suivant la phase de la sinusoïde, elle peut être reconstructible ou non. C'est pour ça que Nyquist dit que FE doit être strictement supérieure à 2F, et pas seulement supérieure ou égale.

Citation de scare :

Avec deux points , on ne sait pas à quoi ressemble le signal, ça peut être une rampe , un signal carré, un signal continu, un pulse, la barbe à will zégal etc etc .... et la fréquence ca peut être tout et n'importe quoi ...

C'est quoi la transformée de Fourier de la barbe de Will ?

Citation :

Suivant la phase de la sinusoïde, elle peut être reconstructible ou non.

Je ne vois pas comment.

Que les deux échantillons soient à 0°-180 ou 10°-190 ou 20°-200° ou 30°-210° etc etc, ils resterons toujours à la même position, donc cela n'est pas reconstructible..

EDIT : Oui effectivement selon le déphasage des échantillons par rapport à la sinusoïde on retrouve un signal triangulaire, donc on peut !!!!

On pourrait aussi se poser la question de ce qu'il se passe à F = FE / 4, soit la fréquence 11025 Hz, logiquement il y a quatre échantillons qui ne bougent pas.

Mais cela dessine forcément un signal dont la fréq fondamentale permet de reconstruire la sinusoïde via un passe bas.

Citation :

C'est quoi la transformée de Fourier de la barbe de Will ? 

Un bruit brun 

Citation :

si on a un échantillon à +Vmax, suivi d'un à -Vmax, c'est une composante à 22kHz, et c'est LA sinusoïde qui passe par ces deux points. Aucune sinusoïde de fréquence plus basse ne peut passer par ces 2 points.

Ce cas ne peut arriver que à F=F/2 avec un déphasage des échantillon de 90°,  c'est peut petre de ce cas là dont parle Zerosquare !! 

DAns ce cas on a un signal triangulaire et il est possible logiquement de retrouver la sinusoïde.

EDIT : et finalement j'ai l'impression que l'on ne peut pas reconstruire que dans le cas où les deux échantillons sont à 0° et 180 ° ou l'on a un signal "plat" sans la fondamentale.

Scare, as-tu eu l'occasion d'entendre un sinus de 15kHz enregistré sur un bon magnéto à bandes ? Moi oui, et je peux t'assurer que c'est plus inquiétant que le problème de reconstruction des 20kHz à une Fe de 44,1 !

JM