Cette semaine, nous allons nous pencher sur deux manières supplémentaires d’effectuer des substitutions d’accords : la substitution par accord relatif et la substitution par échange tonal. Mais avant tout, nous allons compléter l’article précédent et en terminer avec les substitutions de dominantes.
La dominante sans fondamentale
En effet, il nous semble important de souligner que l’accord de dominante d’une tonalité donnée peut être remplacé par l’accord du degré VII basé sur la sensible. On se rappellera que ce dernier inclut le triton (cf. articles 1 et 9) et l’on constatera qu’en dehors de la fondamentale, la triade du degré VII reprend toutes les notes de l’accord de septième de dominante, tel qu’on peut le voir dans l’exemple suivant :
On désigne donc souvent la triade du degré VII comme une dominante sans fondamentale. La substitution de l’accord de degré V par celui de degré VII constitue d’ailleurs une exception à la règle que nous allons maintenant aborder.
La substitution par accord relatif
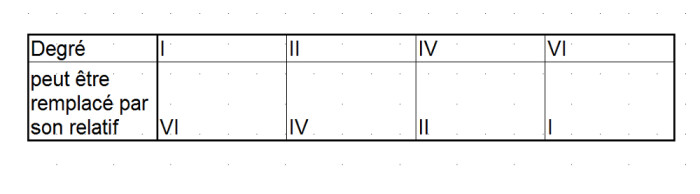
L’étude des gammes relatives (article 3) nous a montré que deux gammes relatives entre elles sont composées d’exactement les mêmes notes, avec leurs toniques séparées d’un ton et demi. À partir de là, on peut considérer que chaque accord d’une tonalité donnée peut être remplacé par son relatif mineur ou majeur (cf. par exemple le remplacement du degré IV par le degré II dans la progression IV-V-I dans l’article 14)
Le tableau ci-dessous présente un rappel des substitutions possibles dans ce cadre-là :
Comme je vous l’ai annoncé dans le paragraphe précédent, l’accord de degré V présente une exception à cette règle, en conséquence de quoi il ne figure pas dans ce tableau. En effet, son accord relatif serait celui basé sur le degré III. Or, ce dernier, malgré son statut de relatif au degré V, est en effet considéré comme un accord de tonique (cf. article 14). Il ne peut donc pas remplacer l’accord de dominante. Logique, non ?
Et c’est encore plus vrai lorsque l’on considère les accords de septième. Dans ce cas, l’accord de dominante inclut le fameux triton (cf. article 9), ce que ne fait pas l’accord de septième basé sur le degré III.
La substitution tonale
Mais nous pouvons aller encore plus loin dans les échanges d’accords entre gammes. Dans l’article 15, nous avions vu que nous pouvions remplacer, dans la progression II-V-I, l’accord du degré II par une dominante secondaire, basée sur la même fondamentale. Eh bien, on peut remplacer l’accord de chaque degré d’une gamme donnée par son équivalent dans les gammes parallèles. Pour information, on appelle « gammes parallèles » les gammes qui possèdent la même tonique. Ainsi les gammes de Mi majeur, Mi mineur naturelle, Mi mineur harmonique et Mi mineur mélodique sont toutes des gammes parallèles de Mi.
Alors bien sûr, il sera généralement déconseillé de remplacer un accord de degré I majeur par son homologue mineur dans une cadence parfaite finale, à moins de souhaiter imprimer un changement radical de caractère à son morceau.
Ci-dessous, deux exemples de substitution tonale :
Mais je vous propose d’expérimenter également par vous-mêmes avec d’autres progressions et d’autres remplacements ! Comme vous le constaterez sans doute, l’apport de notes étrangères à la tonalité de base apportera son lot de couleurs sonores nouvelles, et vous donnera très certainement l’envie de faire moduler parfois votre morceau dans une autre tonalité.
Et la modulation, c’est justement ce que nous aborderons dans notre prochain article !