Analyse d'un circuit simple : Vol + Tone (partie 3) - L'électronique pour le musicien partie 14

Le dernier article de cette série nous avait lais­sés sur une conclu­sion qui allait rebattre les cartes, et chan­ger les quelques notions que nous avions établies sur le circuit volume et tona­lité. Nous étions arrivé au point suivant : un micro de guitare, dans sa réalité physique, réunit des proprié­tés induc­tive (L), résis­tive ®, et capa­ci­tive ©. Pour mémoire, nous avions terminé l’ar­ticle sur ce schéma où l’on voit le micro, modé­lisé à la fois comme une source de tension alter­na­tive (V1) avec en série une induc­tance (L1) et une résis­tance (R1), et en paral­lèle un conden­sa­teur (C1).

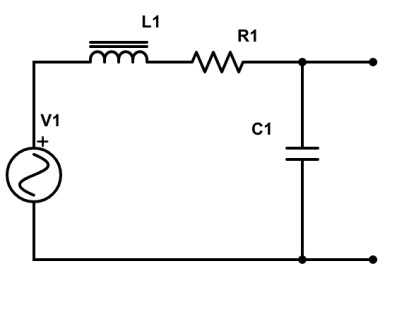
Le micro de notre guitare ainsi modé­lisé, on lui avait raccordé le circuit volume et tona­lité, et j’avais noté qu’il faudrait aussi penser à l’im­pé­dance d’en­trée de l’am­pli­fi­ca­teur, et la capa­cité (faible mais non négli­geable) du câble qui relie l’ins­tru­ment à l’am­pli­fi­ca­teur.

Aujour­d’hui, nous allons voir comment ces diffé­rents éléments inter­agissent entre eux et l’im­pact qu’ils auront sur la bande passante de l’ins­tru­ment. Pour ce faire, nous allons nous baser sur un exemple précis, tiré du réel. Celui-ci nous permet­tra d’abor­der des notions tech­niques à travers un exemple concret. Cet exemple sera ma guitare (une Fender Mustang), dont nous consi­dè­re­rons un seul micro, le micro cheva­let et son inter­ac­tion avec le système volume et tona­lité.

Nous procé­de­rons en deux temps, et avec deux outils. Dans un premier temps, en prenant des mesures de chaque compo­sant dans cette guitare, de façon à asso­cier des valeurs à notre schéma. Nous utili­se­rons pour cela un LCRmètre, qui nous permet­tra d’ef­fec­tuer des mesures d’in­duc­tance, capa­cité et résis­tance, en régime alter­na­tif. Dans un second temps, avec le free­ware LTSpice, nous modé­li­se­rons le circuit obtenu, afin de simu­ler son effet sur la bande passante.

Mais dans un premier temps, complé­tons notre schéma !

Tu seras bien­venu schéma

Je commence en préci­sant qu’après avoir jeté toute mon éner­gie dans ce titre à jeu de mot pourri, et par manque d’ins­pi­ra­tion, tous les autres titres provien­dront de chan­sons qu’a inter­pré­tées M. Florent Pagny. Merci qui ?

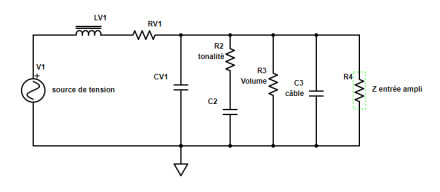
Repre­nons. Voici le schéma complet, avec tous les compo­sants. Analy­sons le ! Sur la partie gauche, on retrouve tous les éléments que nous avons vu jusqu’ici. Le micro est modé­lisé comme une souce de tension V1. Vous remarquez que l’in­duc­tance, la résis­tance et la capa­cité du micro sont nommées de façon à faire réfé­rence à la source V (LV1, RV1, CV1). On retrouve ensuite le potard de tona­lité (symbo­lisé par la résis­tance R2) et son conden­sa­teur C2. Puis le poten­tio­mètre de volume (résis­tance R3) et, en paral­lèle, un nouveau conden­sa­teur : c’est la capa­cité du câble (C3). Pour termi­ner, une résis­tance supplé­men­taire symbo­lise l’im­pé­dance d’en­trée de l’am­pli­fi­ca­teur (Zin, symbo­lisé ici par R4).

Le schéma est alors à peu près complet (il lui manque une repré­sen­ta­tion de l’in­duc­tance géné­rée par les courants de Foucault, de la résis­tance série des câbles, mais nous pouvons nous passer de ces facteurs à notre niveau…). Notre schéma est assez touffu : plus loin dans l’ar­ticle, nous procé­de­rons à une simpli­fi­ca­tion en réunis­sant ensemble certains compo­sants de même natu­re… Mais pour l’ins­tant, nous allons passer à l’as­si­gna­tion de valeurs.

Les p’tites cuillères, tout c’qu’à vos yeux a d’la valeur

Comme expliqué dans l’in­tro, nous allons tirer ces valeurs du réel. Il va donc falloir mesu­rer les valeurs des diffé­rents compo­sants présents dans cette guitare.

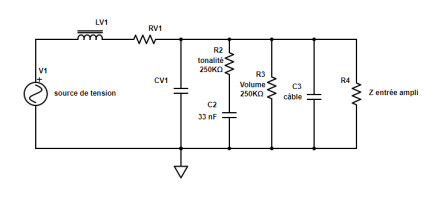
Commençons par le plus simple : les poten­tio­mètres et le conden­sa­teur. Il suffit de faire un relevé : les potards de volume et tone font 250 kΩ, le conden­sa­teur 33 nF (nano Farad). Sur le schéma on va consi­dé­rer, pour commen­cer, que les deux potards sont sur 10, et donc on assigne aux résis­tances R2 et R3 la valeur 250 kΩ.

Pour le reste, il va nous falloir procé­der à des mesures avec un LCRmètre. Commençons par le micro. La mesure révèle une induc­tance de 4,3 H (Henries), une résis­tance de 6 kΩ et une capa­cité de 185 pF (pico Farad) :

Mesu­rons ensuite le câble : il s’agit d’un câble fait maison, avec du Canare GS-6. Il mesure 5 mètres de long. On obtient une capa­cité de 852 pF. Pour compa­rer, je mesure aussi un câble Yellow Cable d’une longueur simi­laire que j’ai sous la main. Il mesure 357 pF. On se servira de cette donnée pour voir si le câble crée une diffé­rence vrai­ment marquante. Comme nous l’avons déjà noté, la résis­tance du câble est si faible (moins de 1 Ω) que nous l’igno­rons dans cette expé­rience.

Pour finir, je vais suppo­ser que l’en­trée de l’am­pli à un impé­dance d’en­vi­ron 1 MΩ, ce qui est une approxi­ma­tion assez clas­sique. On ajoute tout cela, et notre schéma est complet.

Main­te­nant, il y a moyen de le simpli­fier…

Dites-le simple­ment au lieu d’être méchants

Quand on regarde ce schéma on remarque qu’il y a beau­coup de compo­sants simi­laires qui sont effec­ti­ve­ment montés en paral­lèle, par exemple C1 et C3, même si sur le schéma R2 et R3 sont repré­sen­tées entre eux. Ici, il est donc possible d’ef­fec­tuer quelques calculs pour combi­ner ces compo­sants paral­lèles en un seul, et de déter­mi­ner sa valeur.

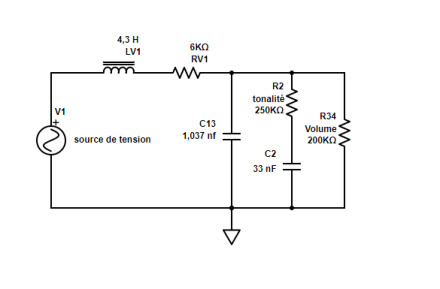
Donc C1 et C3 forme une seule capa­cité (nommée ici C13), de 185 + 852 = 1037 pF (ou 1,037 nF). De la même façon R3 (le poten­tio­mètre de volume) a été regroupé avec R4 (impé­dance d’en­trée) – ce qui nous donne une résis­tance totale de 200 kΩ.

Et main­te­nant que nous avons modé­lisé notre circuit par un schéma compact, nous pouvons passer à la simu­la­tion.

Comme d’ha­bi­tude, on fera semblant

LT Spice est un programme de simu­la­tion élec­tro­nique. C’est celui que j’ai choisi d’uti­li­ser pour cet article car il est simple à prendre en main, et surtout qu’il est gratuit : l’idée ici est de vous donner envie de vous lancer, et d’ex­pé­ri­men­ter par vous même. Nous commençons donc par entrer le schéma que nous avons obtenu dans ce logi­ciel. Ensuite, nous pouvons effec­tuer une simu­la­tion d’un sweep, sur une bande passante que nous avons réglé de 50 à 5 kHz (bande passante suffi­sante pour tester un circuit comme celui-ci).

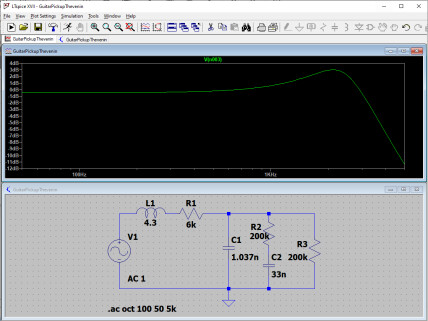
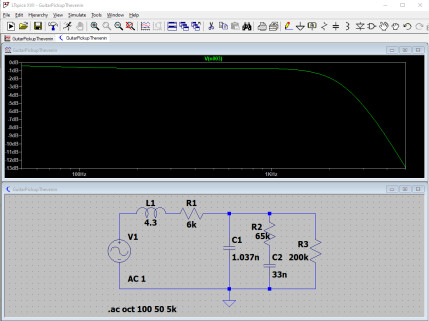
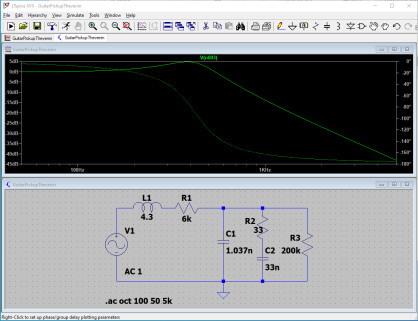
Ce qui frappe immé­dia­te­ment, ce n’est pas tant que notre circuit agit comme un filtre passe-bas, qui atté­nue forte­ment les fréquences au-dessus de 3 kHz, mais c’est la présence d’une « cloche » avec un pic de presque +6 dB à 2,2 kHz.

J’avais évoqué dans l’ar­ticle précé­dent le fait que le micro de guitare, en lui-même, avec son induc­tance sa résis­tance et sa capa­cité, forme un filtre réson­nant passe bas du second ordre. Le mot impor­tant dans cette descrip­tion tech­nique est, bien entendu, « réson­nant ». Cette réson­nance provient de l’in­ter­ac­tion de l’in­duc­tance et des capa­ci­tés présentes dans le circuit. Nous n’irons pas, à ce stade de la série, dans les détails du carac­tère réson­nant du couple LC, mais notez au moins qu’un couple LC monté en paral­lèle forme la base la plus simple d’un oscil­la­teur. Un couple LC va donc natu­rel­le­ment déve­lop­per, par son inter­ac­tion, une fréquence de réso­nance. Dans notre circuit Vol + Tone, il va donc permettre l’am­pli­fi­ca­tion en tension du signal à une fréquence donnée, fréquence qui dépend de la valeur des deux compo­sants. Cette ampli­fi­ca­tion en tension sera d’une ampli­tude plus ou moins grande (là aussi dépen­dante de la valeur des compo­sants), ampli­tude que l’on symbo­lise par la lettre Q.

NB : nous avions toujours affirmé que les compo­sants passifs ne permet­tait pas d’am­pli­fier un signal. En vérité, certains montages, ou certains compo­sants – les tran­for­ma­teurs – permettent d’am­pli­fier la tension d’un signal, mais cause alors une dimi­nu­tion de l’in­ten­sité du courant. La puis­sance du signal (produit de la tension et de l’in­ten­sité) reste donc inchan­gée.

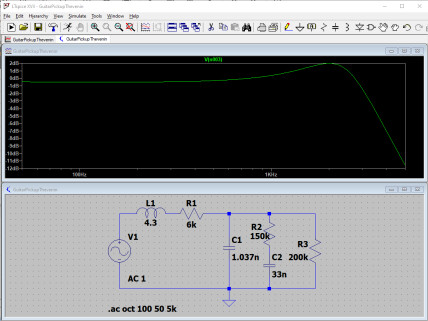
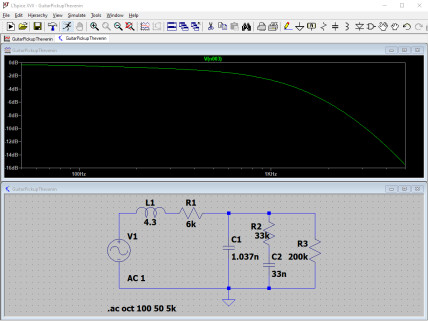
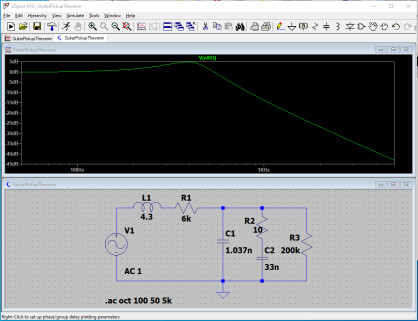
Que se passe-t-il si l’on tourne le poten­tio­mètre de tona­lité ? Voyez ci-dessous pour des valeurs de 200 kΩ, 150 kΩ, 100 kΩ, 65 kΩ et 33 kΩ (pour un meilleur affi­chage, cliquez sur les images) : 

 Plutôt qu’un chan­ge­ment de la fréquence de coupure du filtre passe bas, on assiste à une dimi­nu­tion de Q. L’am­pli­tude de la réson­nance dimi­nue : plus la résis­tance est faible, plus le conden­sa­teur de 33 nF se retrouve effec­ti­ve­ment en paral­lèle avec les capa­ci­tés du câble et du micro et s’ajoute à elles, et plus la valeur de Q dimi­nue.

En vérité, notre circuit Vol + Tone fonc­tionne comme une « loupe » audi­tive, en accen­tuant certaines fréquences de la guitare élec­trique. Cette accen­tua­tion parti­cipe au timbre si spéci­fique, si recon­nais­sable à nos oreilles, de cet instru­ment. La dimi­nu­tion de cette accen­tua­tion change notre percep­tion, et nous parvient comme une atté­nua­tion de ses aigus. Que se passe-t-il si l’on dimi­nue la résis­tance du poten­tio­mètre encore plus bas ?

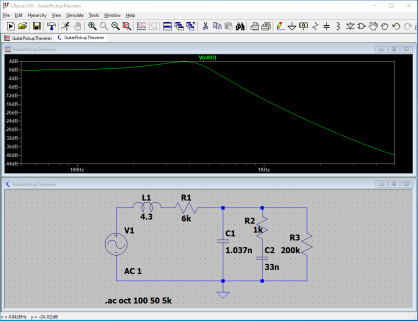
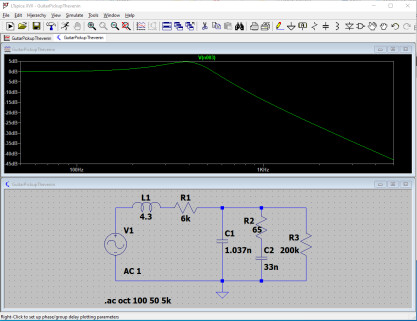
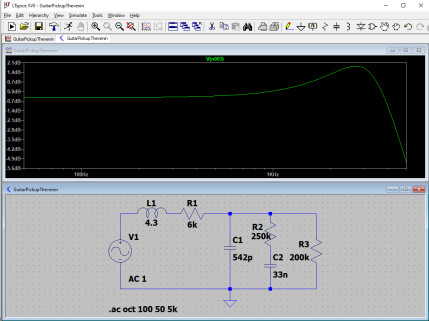
 Valeurs : 1 kΩ, 65 Ω, 33 Ω, 10 Ω

On voit appa­raître une nouvelle accen­tua­tion ! Cette fois-ci aux alen­tours de 400 Hz, entre les basses et les bas-médiums. En vérité, un poten­tio­mètre de tona­lité fonc­tionne presque, toutes propor­tions gardées, comme une petite wah inté­grée, qui permet le dépla­ce­ment d’une fréquence de réson­nance du haut-médium vers le bas-médium.

Reve­nons main­te­nant au câble : sa capa­cité, sa longueur, cela joue-t-il vrai­ment un rôle ?

Restent les murs porteurs, pour se couper du vent, pour tenir la longueur

Eh bien oui, on l’aura compris, vu qu’il contri­bue à plus de la moitié de la valeur de la charge capa­ci­tive dans le couple réson­nant LC, le câble est très impor­tant, et sa longueur, comme sa fabri­ca­tion, est un facteur impor­tant. Voici les résul­tats compa­rés de mon câble DIY et du câble Yellow Cable, avec les potards à 10 :

On voit bien comment la fréquence de réson­nance se déplace plus dans l’aigu avec le Yellow Cable. Mais les guita­ristes et les bassistes le savent déjà : les câbles, leur longueur, leur qualité, joue sur la colo­ra­tion du son.

La prochaine fois, nous conclu­rons cette étude du système Vol + Tone en étudiant les inter­ac­tions du poten­tio­mètre de volume, et celles d’autres possi­bi­li­tés de cablâges, dont le fameux « 50's wiring ».